《電力》〈配電〉[R05下:問16]百分率インピーダンスと過電流遮断器の整定に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

図のような系統において，昇圧用変圧器の容量は\( \ 30 \ \mathrm {MV\cdot A} \ \)，変圧比は\( \ 11 \ \mathrm {kV} / 33 \ \mathrm {kV} \ \)，百分率インピーダンスは自己容量基準で\( \ 7.8 \ \mathrm {％} \ \)，計器用変流器\( \ \left( \mathrm {CT} \right) \ \)の変流比は\( \ 400 \ \mathrm {A} / 5 \ \mathrm {A} \ \)である。系統の点\( \ \mathrm {F} \ \)において，三相短絡事故が発生し，\( \ 1 \ 800 \ \mathrm {A} \ \)の短絡電流が流れたとき，次の(a)及び(b)の問に答えよ。

ただし，\( \ \mathrm {CT} \ \)の磁気飽和は考慮しないものとする。

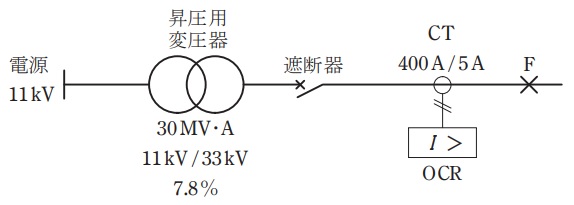
(a)　系統の基準容量を\( \ 10 \ \mathrm {MV\cdot A} \ \)としたとき，事故点\( \ \mathrm {F} \ \)から電源側をみた百分率インピーダンスの値\( \ \mathrm {[％]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 5.6 \ \)　　(2)　\( \ 9.7 \ \)　　(3)　\( \ 12.3 \ \)　　(4)　\( \ 29.2 \ \)　　(5)　\( \ 37.0 \ \)

(b)　過電流継電器\( \ \left( \mathrm {OCR} \right) \ \)を\( \ 0.09 \ \mathrm {s} \ \)で動作させるには，\( \ \mathrm {OCR} \ \)の電流タップ値を何アンペアの位置に整定すればよいか，正しいものを次の(1)～(5)のうちから一つ選べ。

ただし，\( \ \mathrm {OCR} \ \)のタイムレバー位置は\( \ 3 \ \)に整定されており，タイムレバー位置\( \ 10 \ \)における限時特性は図示のとおりである。

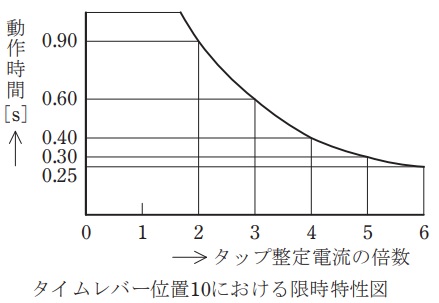
　(1)　\( \ 3.0 \ \mathrm {A} \ \)　　(2)　\( \ 3.5 \ \mathrm {A} \ \)　　(3)　\( \ 4.0 \ \mathrm {A} \ \)　　(4)　\( \ 4.5 \ \mathrm {A} \ \)　　(5)　\( \ 5.0 \ \mathrm {A} \ \)

【ワンポイント解説】

百分率インピーダンスを求めた後，短絡電流を求め過電流遮断器の整定値を求める問題です。
(a)は変圧器の百分率インピーダンスの値を使用しないという引っかけ要素がありクセがある問題ですが，特に(b)の内容に苦戦する受験生が多いかと予想されます。整定値の考え方は慣れの要素が大きいので，解説の中で理解するようにして下さい。
本問は平成18年問17からの再出題となります。

1.オーム法からパーセントインピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \)，基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)，基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると，\( \ Z \ \mathrm {[\Omega ]} \ \)の百分率インピーダンス（パーセントインピーダンス）\( \ ％Z \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 　(定義) \\[ 5pt ] &=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ] &=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100　　 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\] となります。

2.百分率インピーダンスの短絡電流計算
ある地点から電源側を見た百分率インピーダンスを\( \ ％Z \ \mathrm {[％]} \ \)とすると，その点での三相短絡電流\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は，基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)を用いて，
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}}{％Z／100} \\[ 5pt ] &=&\frac {100I_{\mathrm {n}}}{％Z} \\[ 5pt ] \end{eqnarray}
\] で求められます。

※百分率インピーダンスの定義式等を用いて\( \ \displaystyle I_{\mathrm {s}}=\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \ \)から上式を求めることはできますが，試験時には暗記しておいた方が良いと思います。
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}I_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}}\times I_{\mathrm {n}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}\times 100}\times 100I_{\mathrm {n}} \\[ 5pt ] &=&\frac {100I_{\mathrm {n}}}{％Z_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\]

【解答】

(a)解答：(2)
昇圧用変圧器二次側の定格電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)は，基準容量\( \ P_{\mathrm {n}}=10 \ \mathrm {[MV\cdot A]} \ \)，基準電圧\( \ V_{\mathrm {n}}=33 \ \mathrm {[kV]} \ \)より，
\[
\begin{eqnarray}
I_{\mathrm {n}}&=&\frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ] &=&\frac {10\times 10^{6}}{\sqrt {3}\times 33\times 10^{3}} \\[ 5pt ] &≒&175.0 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であり，三相短絡電流\( \ I_{\mathrm {s}}=1 \ 800 \ \mathrm {[A]} \ \)なので，事故点\( \ \mathrm {F} \ \)から電源側をみた百分率インピーダンス\( \ ％Z \ \mathrm {[％]} \ \)は，ワンポイント解説「2.百分率インピーダンスの短絡電流計算」より，
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {100I_{\mathrm {n}}}{％Z} \\[ 5pt ] ％Z&=&\frac {100I_{\mathrm {n}}}{I_{\mathrm {s}}} \\[ 5pt ] &=&\frac {100\times 175.0}{1 \ 800} \\[ 5pt ] &≒&9.72 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
\( \ \mathrm {CT} \ \)の変流比は\( \ 400 \ \mathrm {A} / 5 \ \mathrm {A} \ \)なので，三相短絡時の\( \ \mathrm {CT} \ \)二次側の電流値\( \ I_{\mathrm {s2}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {s2}}&=&\frac {5}{400}I_{\mathrm {s}} \\[ 5pt ] &=&\frac {5}{400}\times 1 \ 800 \\[ 5pt ] &=&22.5 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。本問において，\( \ \mathrm {OCR} \ \)のタイムレバー位置は\( \ 3 \ \)となっているので，動作時間は\( \ \displaystyle \frac {3}{10} \ \)となるため図1のようになり，\( \ \mathrm {OCR} \ \)を\( \ 0.09 \ \mathrm {s} \ \)で動作させるには，\( \ I_{\mathrm {s2}} \ \mathrm {[A]} \ \)の値がタップ整定電流の\( \ 5 \ \)倍の値でなければならないことがわかる。したがって，タップ整定電流\( \ I_{\mathrm {t}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {t}}&=&\frac {I_{\mathrm {s2}}}{5} \\[ 5pt ] &=&\frac {22.5}{5} \\[ 5pt ] &=&4.5 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。