Contents
【問題】
【難易度】★★★★★(難しい)
図1のような\( \ \mathrm {T} \ \)形回路(\( \ 1 \ \)相分)があり,抵抗\( \ r=20 \ \mathrm {\Omega } \ \),リアクタンス\( \ x=80 \ \mathrm {\Omega } \ \),アドミタンス\( \ Y=0.000 \ 7 \ \mathrm {S} \ \)である。\( \ V_{\mathrm {r1}}=150 \ \mathrm {kV} \ \),\( \ I_{\mathrm {r}}=400 \ \mathrm {A} \ \),負荷の力率(遅れ)\( \ \displaystyle \cos \theta _{\mathrm {r}}=\frac {\sqrt {3}}{2} \ \)のとき,次の(a)及び(b)の問に答えよ。
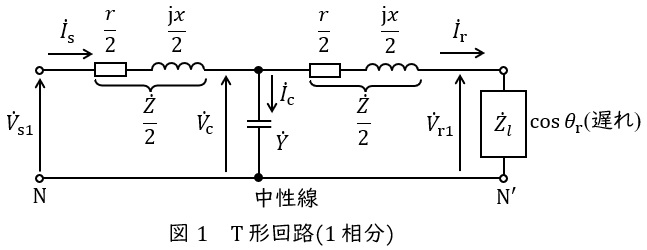
(a) \( \ V_{\mathrm {c}} \ \mathrm {[kV]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 134.2 \ \) (2) \( \ 152.3 \ \) (3) \( \ 161.9 \ \) (4) \( \ 172.0 \ \) (5) \( \ 180.4 \ \)
(b) \( \ V_{\mathrm {s1}} \ \mathrm {[kV]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 145.9 \ \) (2) \( \ 155.4 \ \) (3) \( \ 160.6 \ \) (4) \( \ 170.1 \ \) (5) \( \ 180.7 \ \)
【ワンポイント解説】
\( \ \mathrm {T} \ \)形回路を用いた電圧の導出に関する問題です。
(b)は\( \ 1 \ \)種の二次試験で出題されてもおかしくないような問題で,受験生に\( \ 10 \ \)分程度で解かせるにはかなり厳しい問題であったかと思います。
\( \ 1 \ \)種取得を目指す方は別ですが,現実的には近似解に示すような近似式を用いた計算で正答を選択できれば十分かと思います。
1.抵抗,コイル,コンデンサのインピーダンスとアドミタンス
抵抗\( \ R \ \mathrm {[\Omega ]} \ \),コイル\( \ L \ \mathrm {[H]} \ \),コンデンサ\( \ C \ \mathrm {[F]} \ \)があり,電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき,それぞれのインピーダンス\( \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ]
{\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ]
{\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,アドミタンス\( \ \mathrm {[S]} \ \)はインピーダンスの逆数なので,
\[
\begin{eqnarray}
{\dot Y}_{\mathrm {R}}&=&\frac {1}{R}&& \\[ 5pt ]
{\dot Y}_{\mathrm {L}}&=&\frac {1}{\mathrm {j}\omega L}&=&\frac {1}{\mathrm {j}2\pi f L} \\[ 5pt ]
{\dot Y}_{\mathrm {C}}&=&\mathrm {j}\omega C&=&\mathrm {j}2\pi f C \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
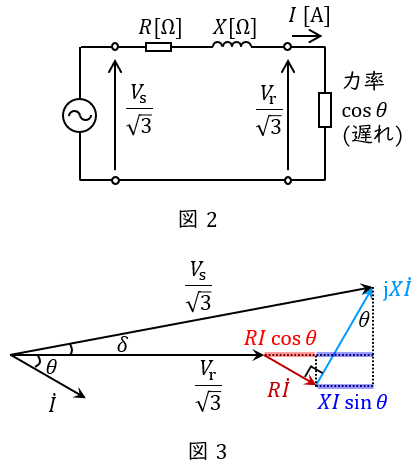
2.三相\( \ 3 \ \)線式送電線の電圧降下の近似式
三相回路においては,一相分の等価回路及びベクトル図は図2及び図3のように描くことができ,送電端電圧と受電端電圧の位相差\( \ \delta \ \mathrm {[rad]} \ \)が無視できるぐらい小さいとしたときの電圧降下\( \ \varepsilon \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
\frac {V_{\mathrm {s}}}{\sqrt {3}}&≃&\frac {V_{\mathrm {r}}}{\sqrt {3}}+RI\cos \theta +XI\sin \theta \\[ 5pt ]
\frac {V_{\mathrm {s}}}{\sqrt {3}}-\frac {V_{\mathrm {r}}}{\sqrt {3}}&=&RI\cos \theta +XI\sin \theta \\[ 5pt ]
V_{\mathrm {s}}-V_{\mathrm {r}}&=&\sqrt {3}\left( RI\cos \theta +XI\sin \theta \right) \\[ 5pt ]
\varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
【解答】
(a)解答:(3)
[精密解]
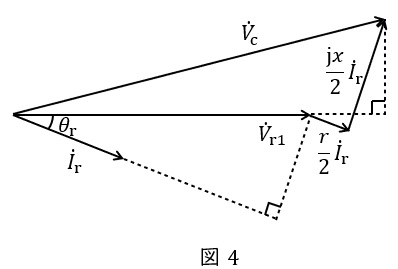
題意に沿ってベクトル図を描くと図4のようになり,\( \ \sin \theta _{\mathrm {r}} \ \)は,
\[
\begin{eqnarray}
\sin \theta _{\mathrm {r}} &=&\sqrt {1-\cos ^{2} \theta _{\mathrm {r}}} \\[ 5pt ]
&=&\sqrt {1-\left( \frac {\sqrt {3}}{2}\right) ^{2}} \\[ 5pt ]
&=&\frac {1}{2} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ {\dot I}_{\mathrm {r}} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {r}} &=&I_{\mathrm {r}}\cos \theta _{\mathrm {r}}-\mathrm {j}I_{\mathrm {r}}\sin \theta _{\mathrm {r}} \\[ 5pt ]
&=&400\times \frac {\sqrt {3}}{2}-\mathrm {j}400\times \frac {1}{2} \\[ 5pt ]
&≒&346.410-\mathrm {j}200 \\[ 5pt ]
\end{eqnarray}
\]
となる。図4より,\( \ {\dot V}_{\mathrm {c}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {c}} &=&{\dot V}_{\mathrm {r1}}+\frac {r}{2}{\dot I}_{\mathrm {r}}+\mathrm {j}\frac {x}{2}{\dot I}_{\mathrm {r}} \\[ 5pt ]
&=&150\times 10^{3}+\frac {20}{2}\times \left( 346.410-\mathrm {j}200\right) +\mathrm {j}\frac {80}{2}\times \left( 346.410-\mathrm {j}200\right) \\[ 5pt ]
&=&150 \ 000+3 \ 464.10-\mathrm {j}2 \ 000 +\mathrm {j}13 \ 856.4+8 \ 000 \\[ 5pt ]
&≒&161 \ 464+\mathrm {j}11 \ 856.4 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となり,その大きさ\( \ V_{\mathrm {c}} \ \mathrm {[kV]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {c}} &≒&\sqrt {161 \ 464^{2}+11 \ 856.4^{2}} \\[ 5pt ]
&≒&161 \ 899 \ \mathrm {[V]} → 161.9 \ \mathrm {[kV]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
[近似解]
\( \ {\dot V}_{\mathrm {c}} \ \)と\( \ {\dot V}_{\mathrm {r1}} \ \)の位相差が十分に小さいと考えれば,
\[
\begin{eqnarray}
V_{\mathrm {c}} &=&V_{\mathrm {r1}}+\frac {r}{2}I_{\mathrm {r}}\cos \theta _{\mathrm {r}}+\frac {x}{2}I_{\mathrm {r}}\sin \theta _{\mathrm {r}} \\[ 5pt ]
&=&150\times 10^{3}+\frac {20}{2}\times 400 \times \frac {\sqrt {3}}{2}+\frac {80}{2}\times 400 \times \frac {1}{2} \\[ 5pt ]
&≒&161 \ 000 \ \mathrm {[V]} → 161 \ \mathrm {[kV]} \\[ 5pt ]
\end{eqnarray}
\]
となり最も近いのは\( \ 161.9 \ \mathrm {kV} \ \)と求められる。
(b)解答:(4)
[精密解]
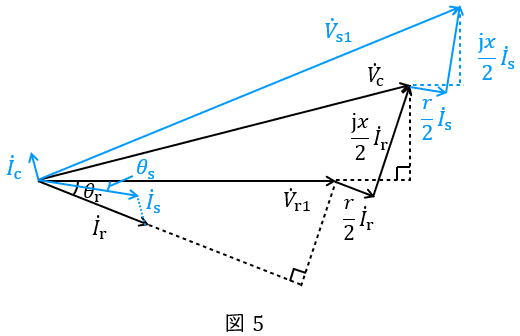
題意に沿ってベクトル図を描くと図5のようになる。電流\( \ {\dot I}_{\mathrm {c}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {c}} &=&\dot Y{\dot V}_{\mathrm {c}} \\[ 5pt ]
&=&\mathrm {j}0.000 \ 7 \times \left( 161 \ 464+\mathrm {j}11 \ 856.4\right) \\[ 5pt ]
&≒&-8.299 \ 48+\mathrm {j}113.025 \\[ 5pt ]
\end{eqnarray}
\]
であるから,電流\( \ {\dot I}_{\mathrm {s}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {s}} &=&{\dot I}_{\mathrm {c}}+{\dot I}_{\mathrm {r}} \\[ 5pt ]
&=&-8.299 \ 48+\mathrm {j}113.025+346.410-\mathrm {j}200 \\[ 5pt ]
&≒&338.111-\mathrm {j}86.975 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,\( \ {\dot V}_{\mathrm {s1}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {s1}} &=&{\dot V}_{\mathrm {c}}+\frac {r}{2}{\dot I}_{\mathrm {s}}+\mathrm {j}\frac {x}{2}{\dot I}_{\mathrm {s}} \\[ 5pt ]
&=&161 \ 464+\mathrm {j}118 \ 56.4+\frac {20}{2}\times \left( 338.111-\mathrm {j}86.975 \right) +\mathrm {j}\frac {80}{2}\times \left( 338.111-\mathrm {j}86.975 \right) \\[ 5pt ]
&≒&161 \ 464+\mathrm {j}118 \ 56.4+3 \ 381.11-\mathrm {j}869.75 +\mathrm {j}13 \ 524.4+3 \ 479 \\[ 5pt ]
&≒&168 \ 324+\mathrm {j}24 \ 511.1 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となり,その大きさ\( \ V_{\mathrm {s1}} \ \mathrm {[kV]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {s1}} &≒&\sqrt {168 \ 324^{2}+24 \ 511.1^{2}} \\[ 5pt ]
&≒&170 \ 100 \ \mathrm {[V]} → 170.1 \ \mathrm {[kV]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
[近似解]
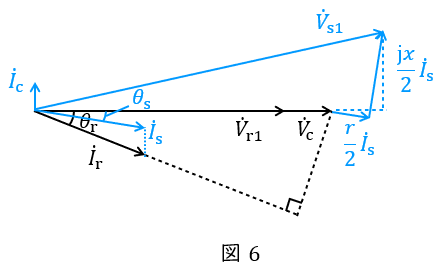
\( \ {\dot V}_{\mathrm {c}} \ \)と\( \ {\dot V}_{\mathrm {r1}} \ \)の位相差が十分に小さいと考え,ベクトル図を描くと図6のようになる。
\( \ {\dot I}_{\mathrm {c}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {c}} &=&\dot Y{\dot V}_{\mathrm {c}} \\[ 5pt ]
&=&\mathrm {j}0.000 \ 7 \times 161 \ 900 \\[ 5pt ]
&=&\mathrm {j}113.33 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ {\dot I}_{\mathrm {s}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {s}} &=&{\dot I}_{\mathrm {c}}+{\dot I}_{\mathrm {r}} \\[ 5pt ]
&=&\mathrm {j}113.33+346.410-\mathrm {j}200 \\[ 5pt ]
&=&346.410-\mathrm {j}86.67 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,\( \ V_{\mathrm {s1}} \ \mathrm {[kV]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {s1}} &≒&V_{\mathrm {c}}+\frac {r}{2}I_{\mathrm {s}}\cos \theta _{\mathrm {s}}+\frac {x}{2}I_{\mathrm {s}}\sin \theta _{\mathrm {s}} \\[ 5pt ]
&≒&161 \ 900+\frac {20}{2}\times 346.410+\frac {80}{2}\times 86.67 \\[ 5pt ]
&≒&168 \ 800 \ \mathrm {[V]} → 168.8 \ \mathrm {[kV]} \\[ 5pt ]
\end{eqnarray}
\]
となり,最も近いのは\( \ 170.1 \ \mathrm {kV} \ \)と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは