《電力》〈水力〉[R07上:問15]調整池式水力発電所における使用水量と有効貯水容量に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図の流況曲線を持つ河川の全流量を使用できる調整池式水力発電所において，発電所の使用流量\( \ \mathrm {[m^{3} /s]} \ \)と調整池の有効貯水容量\( \ \mathrm {[m^{3}]} \ \)について，次の(a)及び(b)の問に答えよ。

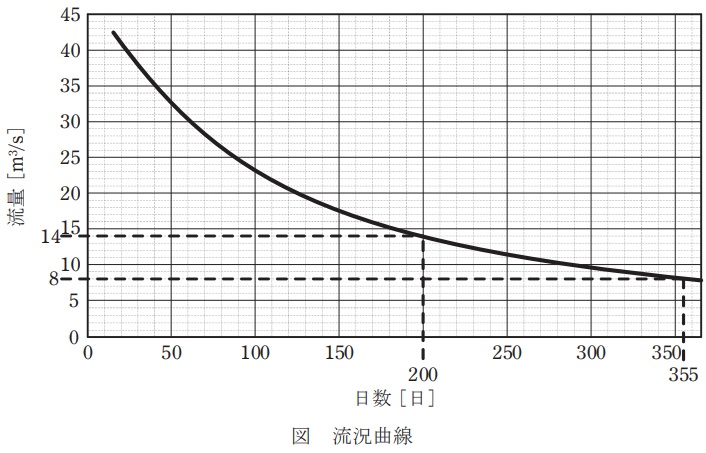
(a)　\( \ 1 \ \)日単位の調整運転を行う場合，上記流況曲線の渇水量\( \ 8 \ \mathrm {m^{3} /s} \ \)において，\( \ 1 \ \)日に\( \ 6 \ \)時間の運転を可能とする最大の使用流量\( \ \mathrm {[m^{3} /s]} \ \)と，当該時間外に調整池に流入する貯水量\( \ \mathrm {[m^{3}]} \ \)の組合せとして，最も近いものを次の(1)～(5)のうちから一つ選べ。

　ここで，当該\( \ 6 \ \)時間の最大使用流量での運転以外の時間は，水車・発電機を停止して調整池に河川の全流量を貯水するものとする。
\[
\begin{array}{ccc}
& 最大使用流量 \ \mathrm {[m^{3} /s]} & 貯水量 \ \mathrm {[m^{3}]} \\
\hline
(1) & 　22.8　 & 　410 \ 400　 \\
\hline
(2) & 　28.8　 & 　518 \ 400　 \\
\hline
(3) & 　34.8　 & 　518 \ 400　 \\
\hline
(4) & 　28.8　 & 　410 \ 400　 \\
\hline
(5) & 　32.0　 & 　518 \ 400　 \\
\hline
\end{array}
\]

(b)　上記流況曲線で\( \ 200 \ \)日以上発生する流量において，小問(a)の最大使用流量で\( \ 1 \ \)日\( \ 8 \ \)時間の運転を可能とするための有効貯水容量\( \ \mathrm {[m^{3}]} \ \)として，最も小さいものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 420 \ 000 \ \)　　(2)　\( \ 500 \ 000 \ \)　　(3)　\( \ 440 \ 000 \ \)　　(4)　\( \ 460 \ 000 \ \)　
　(5)　\( \ 520 \ 000 \ \)

【ワンポイント解説】

調整池式水力発電所の使用水量と有効貯水容量を求める問題です。
特別な公式は使用しませんが，問題文を読みその場で考える読解力を要する問題です。問題慣れの要素も強く，受験生の正答率も低くなるので，焦らずに落ち着いて解きアドバンテージを得るようにしましょう。特に上位資格を目指す方は読解力は必ず必要な能力となります。

【解答】

(a)解答：(5)
\( \ 8 \ \mathrm {m^{3} /s} \ \)で\( \ 24 \ \)時間貯水したものを\( \ 6 \ \)時間で使用するので，このときの使用流量\( \ Q \ \mathrm {[m^{3} /s]} \ \)は，
\[
\begin{eqnarray}
8\times 3 \ 600 \times 24 &=&Q\times 3 \ 600 \times 6 \\[ 5pt ] Q&=&32 \ \mathrm {[m^{3} /s]} \\[ 5pt ] \end{eqnarray}
\] と求められる。また，調整池に流入する貯水量\( \ W \ \mathrm {[m^{3}]} \ \)は，\( \ 18 \ \)時間貯水したときの量なので，
\[
\begin{eqnarray}
W&=&8\times 3 \ 600 \times 18 \\[ 5pt ] &=&518 \ 400 \ \mathrm {[m^{3}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(5)
(a)より運転時の使用水量は\( \ Q=32 \ \mathrm {[m^{3} /s]} \ \)であり，流況曲線において\( \ 200 \ \)日以上発生する流量は\( \ 14 \ \mathrm {m^{3} /s} \ \)であるため，毎秒貯水池から，
\[
\begin{eqnarray}
\Delta Q&=&Q-14 \\[ 5pt ] &=&32-14 \\[ 5pt ] &=&18 \ \mathrm {[m^{3} /s]} \\[ 5pt ] \end{eqnarray}
\] の水が減少していくことになる。したがって，\( \ 8 \ \)時間の運転を可能とするための有効貯水容量\( \ W^{\prime } \ \mathrm {[m^{3}]} \ \)は，
\[
\begin{eqnarray}
W^{\prime }&=&\Delta Q\times 3 \ 600 \times 8 \\[ 5pt ] &=&18\times 3 \ 600 \times 8 \\[ 5pt ] &=&518 \ 400　→　520 \ 000 \ \mathrm {[m^{3}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。