《法規》〈電気施設管理〉[H21:問13]低圧幹線に施設する配電用遮断器に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

図は，三相\( \ 210 \ \mathrm {[V]} \ \)低圧幹線の計画図の一部である。図の低圧配電盤から分電盤に至る低圧幹線に施設する配線用遮断器に関して，次の(a)及び(b)に答えよ。

ただし，基準容量\( \ 200 \ \mathrm {[kV\cdot A]} \ \)・基準電圧\( \ 210 \ \mathrm {[V]} \ \)として，変圧器及びケーブルの各百分率インピーダンスは次のとおりとし，変圧器より電源側及びその他記載の無いインピーダンスは無視するものとする。

　変圧器の百分率抵抗降下\( \ 1.4 \ \mathrm {[％]} \ \)及び百分率リアクタンス降下\( \ 2.0 \ \mathrm {[％]} \ \)
　ケーブルの百分率抵抗降下\( \ 8.8 \ \mathrm {[％]} \ \)及び百分率リアクタンス降下\( \ 2.8 \ \mathrm {[％]} \ \)

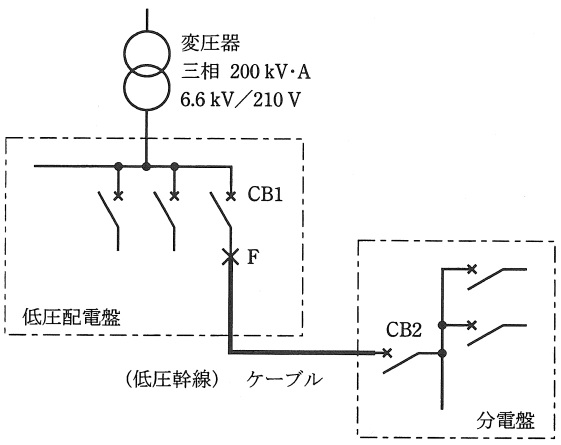
(a)　\( \ \mathrm {F} \ \)点における三相短絡電流\( \ \mathrm {[kA]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 20 \ \)　　(2)　\( \ 23 \ \)　　(3)　\( \ 26 \ \)　　(4)　\( \ 31 \ \)　　(5)　\( \ 35 \ \)

(b)　配線用遮断器\( \ \mathrm {CB1} \ \)及び\( \ \mathrm {CB2} \ \)の遮断容量\( \ \mathrm {[kA]} \ \)の値として，最も適切な組み合わせは次のうちどれか。

ただし，\( \ \mathrm {CB1} \ \)と\( \ \mathrm {CB2} \ \)は，三相短絡電流の値の直近上位の遮断容量\( \ \mathrm {[kA]} \ \)の配線用遮断器を選択するものとする。
\[
\begin{array}{ccc}
& \mathrm {CB1} \ の遮断容量 \ \mathrm {[kA]}　　　 & \mathrm {CB2} \ の遮断容量 \ \mathrm {[kA]}　　　 \\
\hline
(1) & 　5　 & 　2.5　 \\
\hline
(2) & 　10　 & 　2.5　 \\
\hline
(3) & 　22　 & 　5　 \\
\hline
(4) & 　25　 & 　5　 \\
\hline
(5) & 　35　 & 　10　 \\
\hline
\end{array}
\]

【ワンポイント解説】

低圧幹線に施設する配電用遮断器の定格遮断電流を検討する問題です。
実質的には百分率インピーダンスを理解しているかを問う電力の問題です。
合格のためにはぜひ完答しておきたい問題となります。

1.オーム法からパーセントインピーダンス法への変換
基準容量を\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \)，基準電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)，基準電流を\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると，\( \ Z \ \mathrm {[\Omega ]} \ \)の百分率インピーダンス（パーセントインピーダンス）\( \ ％Z \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 　(定義) \\[ 5pt ] &=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ] &=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z}{V_{\mathrm {n}}^{2}}\times 100　　 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\] となります。

2.百分率インピーダンスの短絡電流計算
ある地点から電源側を見た百分率インピーダンスを\( \ ％Z \ \mathrm {[％]} \ \)とすると，その点での三相短絡電流\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)は，基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)を用いて，
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {I_{\mathrm {n}}}{％Z／100} \\[ 5pt ] &=&\frac {100I_{\mathrm {n}}}{％Z} \\[ 5pt ] \end{eqnarray}
\] で求められます。

※百分率インピーダンスの定義式等を用いて\( \ \displaystyle I_{\mathrm {s}}=\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \ \)から上式を求めることはできますが，試験時には暗記しておいた方が良いと思います。
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}{Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}I_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}}\times I_{\mathrm {n}} \\[ 5pt ] &=&\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}} \ \mathrm {[\Omega ]}I_{\mathrm {n}}\times 100}\times 100I_{\mathrm {n}} \\[ 5pt ] &=&\frac {100I_{\mathrm {n}}}{％Z_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\]

【解答】

(a)解答：(2)
変圧器の百分率インピーダンス\( \ ％{\dot Z}_{\mathrm {t}} \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％{\dot Z}_{\mathrm {t}}&=&1.4+\mathrm {j}2.0 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] であるので，その大きさ\( \ ％Z_{\mathrm {t}} \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％Z_{\mathrm {t}}&=&\sqrt {1.4^{2}+2.0^{2}} \\[ 5pt ] &≒&2.441 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となる。また，基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)の大きさは，基準容量\( \ P_{\mathrm {n}}=200 \ \mathrm {[kV\cdot A]} \ \)，基準電圧\( \ V_{\mathrm {n}}=210 \ \mathrm {[V]} \ \)より，
\[
\begin{eqnarray}
I_{\mathrm {n}}&=&\frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ] &=&\frac {200\times 10^{3}}{\sqrt {3}\times 210} \\[ 5pt ] &≒&549.9 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ \mathrm {F} \ \)点における三相短絡電流\( \ I_{\mathrm {s}} \ \mathrm {[kA]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {100I_{\mathrm {n}}}{％Z_{\mathrm {t}}} \\[ 5pt ] &=&\frac {100\times 549.9 }{2.441} \\[ 5pt ] &≒&22 \ 530 \ \mathrm {[A]}　→　22.5 \ \mathrm {[kA]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(4)
(a)解答より，\( \ \mathrm {CB1} \ \)の遮断容量は，\( \ 22.5 \ \mathrm {[kA]} \ \)より大きい\( \ 25 \ \mathrm {[kA]} \ \)が適当である。
次に，\( \ \mathrm {CB2} \ \)の遮断容量を検討すると，\( \ \mathrm {CB2} \ \)から電源側をみた百分率インピーダンス\( \ ％\dot Z \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％\dot Z&=&\left( 1.4+\mathrm {j}2.0\right) +\left( 8.8+\mathrm {j}2.8 \right) \\[ 5pt ] &=&10.2+\mathrm {j}4.8 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] あるので，その大きさ\( \ ％Z \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％Z&=&\sqrt {10.2^{2}+4.8^{2}} \\[ 5pt ] &≒&11.27 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，\( \ \mathrm {CB2} \ \)の二次側における三相短絡電流\( \ I_{\mathrm {s}}^{\prime } \ \mathrm {[kA]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {s}}^{\prime }&=&\frac {100I_{\mathrm {n}}}{％Z} \\[ 5pt ] &=&\frac {100\times 549.9 }{11.27} \\[ 5pt ] &≒&4 \ 879 \ \mathrm {[A]}　→　4.88 \ \mathrm {[kA]} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ \mathrm {CB2} \ \)の遮断容量は，これより大きい\( \ 5 \ \mathrm {[kA]} \ \)が適当である。