《法規》〈電気施設管理〉[H30:問13]変圧器の損失電力及び全日効率に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

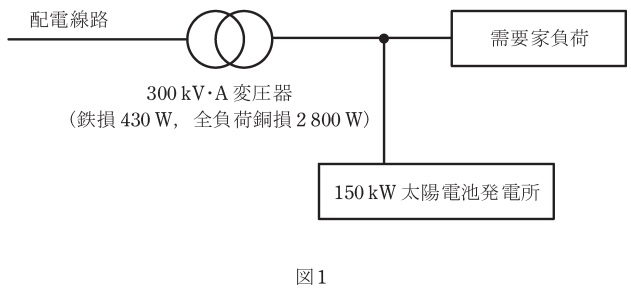
ある需要家では，図1に示すように定格容量\( \ 300 \ \mathrm {kV\cdot A} \ \)，定格電圧における鉄損\( \ 430 \ \mathrm {W} \ \)及び全負荷銅損\( \ 2800 \ \mathrm {W} \ \)の変圧器を介して配電線路から定格電圧で受電し，需要家負荷に電力を供給している。この需要家には出力\( \ 150 \ \mathrm {kW} \ \)の太陽電池発電所が設置されており，図1に示す位置で連系されている。

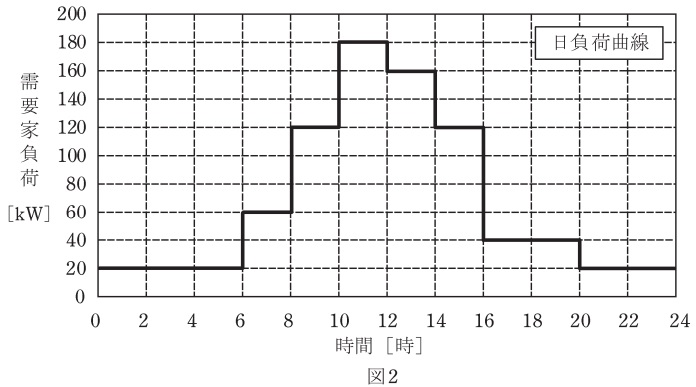
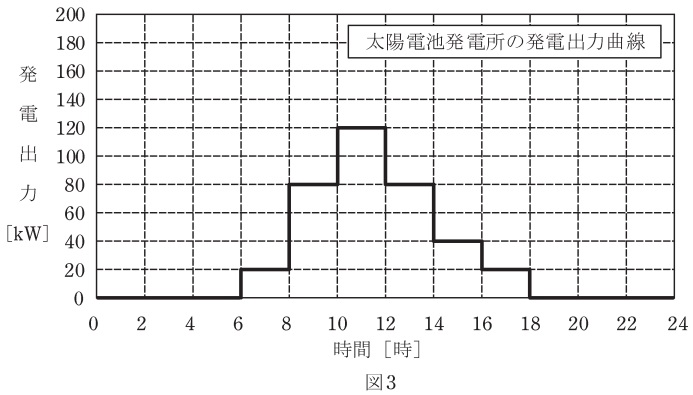
ある日の需要家負荷の日負荷曲線が図2であり，太陽電池発電所の発電出力曲線が図3であるとするとき，次の(a)及び(b)の問に答えよ。

ただし，需要家の負荷力率は\( \ 100 \ ％ \)とし，太陽電池発電所の運転力率も\( \ 100 \ ％ \)とする。なお，鉄損，銅損以外の変圧器の損失及び需要家構内の線路損失は無視するものとする。

(a)　変圧器の1日の損失電力量の値\([\mathrm {kW\cdot h}]\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(10.3\)　　(2)　\(11.8\)　　(3)　\(13.2\)　　(4)　\(16.3\)　　(5)　\(24.4\)

(b)　変圧器の全日効率の値\([％]\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(97.5\)　　(2)　\(97.8\)　　(3)　\(98.7\)　　(4)　\(99.0\)　　(5)　\(99.4\)

【ワンポイント解説】

電力科目，機械科目，法規科目を横断するような応用問題です。計算がやや面倒ですが，丁寧に解くように心掛けましょう。

1.変圧器の効率
変圧器の効率は変圧器の定格出力を\(P_{\mathrm {n}}\)，変圧器の容量\(K\)，鉄損\(p_{\mathrm {i}}\)，定格時の銅損を\(p_{\mathrm {c}}\)とすると，定格負荷時の効率\(\eta _{\mathrm {n}}\)は，
\[
\begin{eqnarray}
\eta _{\mathrm {n}}&=&\frac {出力}{出力＋損失}\times 100 \\[ 5pt ] &=&\frac {P_{\mathrm {n}}}{P_{\mathrm {n}}+p_{\mathrm {i}}+p_{\mathrm {c}}}\times 100 \\[ 5pt ] &=&\frac {K\cos \theta}{K\cos \theta +p_{\mathrm {i}}+p_{\mathrm {c}}}\times 100 \\[ 5pt ] \end{eqnarray}
\] で求められます。

また，利用率が\(\alpha \) (\(\alpha ＜ 1\))の時の効率\(\eta _{\mathrm {m}}\)は，銅損が利用率の\(2\)乗に比例するので，
\[
\begin{eqnarray}
\eta _{\mathrm {m}}&=&\frac {出力}{出力＋損失}\times 100 \\[ 5pt ] &=&\frac {P}{P +p_{\mathrm {i}}+\alpha ^{2}p_{\mathrm {c}}}\times 100 \\[ 5pt ] &=&\frac {\alpha K\cos \theta}{\alpha K\cos \theta +p_{\mathrm {i}}+\alpha ^{2}p_{\mathrm {c}}}\times 100 \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(2)
需要家負荷の日負荷曲線から太陽電池発電所の出力を差し引いたものが変圧器の負荷になるので，変圧器の負荷曲線は図4のようになる。

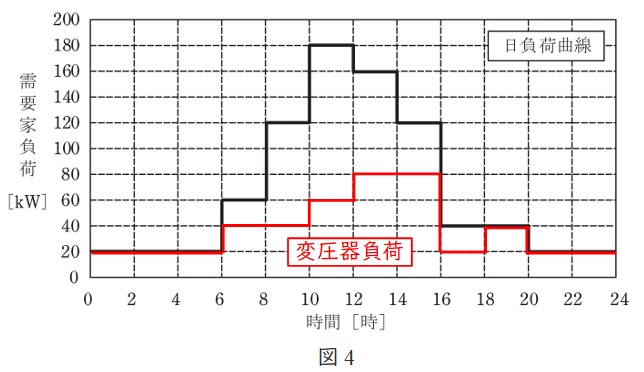
図4より，変圧器負荷の時間数の内訳は，
\[
\begin{eqnarray}
20 \ \mathrm {kW} &：&12 \ \mathrm {h} \\[ 5pt ] 40 \ \mathrm {kW} &：&6 \ \mathrm {h} \\[ 5pt ] 60 \ \mathrm {kW} &：&2 \ \mathrm {h} \\[ 5pt ] 80 \ \mathrm {kW} &：&4 \ \mathrm {h} \\[ 5pt ] \end{eqnarray}
\] であるから，一日の銅損の合計\(p_{\mathrm {c}}\)は，銅損が利用率の\(2\)乗に比例することから，
\[
\begin{eqnarray}
p_{\mathrm {c}}&=&2800\times 10^{-3} \times \left[ \left( \frac {20}{300}\right) ^{2} \times 12 +\left( \frac {40}{300}\right) ^{2} \times 6+\left( \frac {60}{300}\right) ^{2} \times 2+\left( \frac {80}{300}\right) ^{2} \times 4 \right] \\[ 5pt ] &=&\frac {2800\times 10^{-3}}{300^{2}}\times \left( 20^{2} \times 12 +40^{2} \times 6+60^{2} \times 2+80^{2} \times 4 \right) \\[ 5pt ] &=&\frac {2800\times 10^{-3}}{90000}\times \left( 4800 +9600+7200+25600 \right) \\[ 5pt ] &≒&1.4684 \ \mathrm {[kW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] となる。また，一日の鉄損の合計\(p_{\mathrm {i}}\)は，鉄損が負荷により変化しないことから，
\[
\begin{eqnarray}
p_{\mathrm {i}}&=&430\times 10^{-3} \times 24 \\[ 5pt ] &=&10.32 \ \mathrm {[kW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，１日の損失電力量の合計は，
\[
\begin{eqnarray}
p_{\mathrm {i}}+p_{\mathrm {c}}&=&10.32+1.4684 \\[ 5pt ] &≒&11.788　→　11.8 \ \mathrm {[kW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
変圧器の一日の負荷電力量\(P\)は，
\[
\begin{eqnarray}
P&=&20\times 12+40\times 6+60\times 2+80\times 4 \\[ 5pt ] &=&920 \ \mathrm {[kW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] であるから，全日効率\(\eta \)は，ワンポイント解説「1.変圧器の効率」より，
\[
\begin{eqnarray}
\eta&=&\frac {出力}{出力＋損失}\times 100 \\[ 5pt ] &=&\frac {P}{P+p_{\mathrm {i}}+p_{\mathrm {c}}}\times 100 \\[ 5pt ] &=&\frac {920}{920+10.32+1.4684}\times 100 \\[ 5pt ] &≒&98.735　→　98.7 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。