Contents
【問題】
【難易度】★★★☆☆(普通)
界磁磁束を一定に保った直流電動機において,\( \ 0.5 \ \Omega \ \)の抵抗値をもつ電機子巻線と直列に始動抵抗(可変抵抗)が接続されている。この電動機を内部抵抗が無視できる電圧\( \ 200 \ \mathrm {V} \ \)の直流電源に接続した。静止状態で電源に接続した直後の電機子電流は\( \ 100 \ \mathrm {A} \ \)であった。
この電動機の始動後,徐々に回転速度が上昇し,電機子電流が\( \ 50 \ \mathrm {A} \ \)まで減少した。トルクも半分に減少したので,電機子電流を\( \ 100 \ \mathrm {A} \ \)に増やすため,直列可変抵抗の抵抗値を\( \ R_{1} \ \mathrm {[\Omega ]}\)から\( \ R_{2} \ \mathrm {[\Omega ]}\)に変化させた。\( \ R_{1} \ \)及び\( \ R_{2} \ \)の値の組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
ただし,ブラシによる電圧降下,始動抵抗を調整する間の速度変化,電機子反作用及びインダクタンスの影響は無視できるものとする。
\[
\begin{array}{ccc}
& R_{1} & R_{2} \\
\hline
(1) & 2.0 & 1.0 \\
\hline
(2) & 4.0 & 2.0 \\
\hline
(3) & 1.5 & 1.0 \\
\hline
(4) & 1.5 & 0.5 \\
\hline
(5) & 3.5 & 1.5 \\
\hline
\end{array}
\]
【ワンポイント解説】
直流機の電機子回路と重要公式が導入されている非常に良い問題であると思います。導出過程は二種以上の内容となるので,誘導起電力とトルクの式は必ず覚えておいて下さい。
1.直流機の誘導起電力(逆起電力)\(E\)
磁極の数\(p\),電機子導体数\(Z\),電機子巻線並列回路数\(a\),各極の磁束\(\phi \),回転速度\(N\)とすると,直流機の誘導起電力(逆起電力)\(E\)は,
\[
\begin{eqnarray}
E &=&\frac {pZ}{60a}\phi N \\[ 5pt ]
&=&k_{\mathrm {e}}\phi N \\[ 5pt ]
\end{eqnarray}
\]
となり,磁束\(\phi \)と回転速度\(N\)に比例します。
2.直流機のトルク\(T\)
磁極の数\(p\),電機子導体数\(Z\),電機子巻線並列回路数\(a\),各極の磁束\(\phi \),電機子電流\(I_{\mathrm {a}}\)とすると,直流機のトルク\(T\)は,
\[
\begin{eqnarray}
T &=&\frac {pZ}{2\pi a}\phi I_{\mathrm {a}} \\[ 5pt ]
&=&k_{\mathrm {f}}\phi I_{\mathrm {a}} \\[ 5pt ]
\end{eqnarray}
\]
となり,磁束\(\phi \)と電機子電流\(I_{\mathrm {a}}\)に比例します。
【解答】
解答:(4)
題意の直流機の等価回路を図1に示す。図において,\(E\)は逆起電力,\(V\)は電源電圧,\(I_{\mathrm {a}}\)は電機子電流,\(R_{\mathrm {a}}\)は電機子巻線の抵抗値とする。
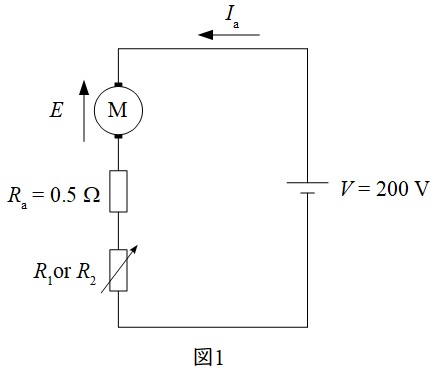
始動時,ワンポイント解説「1.直流機の誘導起電力\(E\)」より,静止状態(回転数零)において逆起電力\(E\)は零であるから,この時の電機子回路は図2のようになる。
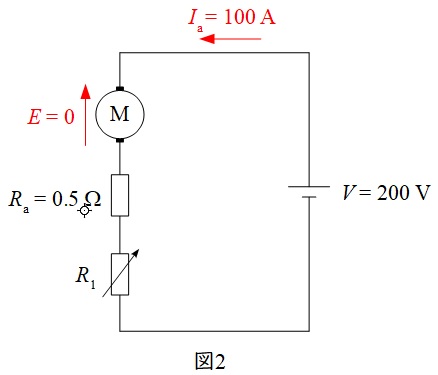
図2の回路方程式から,
\[
\begin{eqnarray}
V &=&\left( R_{\mathrm {a}}+R_{1}\right) I_{\mathrm {a}} \\[ 5pt ]
200 &=&\left( 0.5+R_{1}\right) \times 100 \\[ 5pt ]
0.5+R_{1} &=&2 \\[ 5pt ]
R_{1} &=&1.5 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
次に始動後回転速度が上昇した後の回路図を描くと図3のようになる。
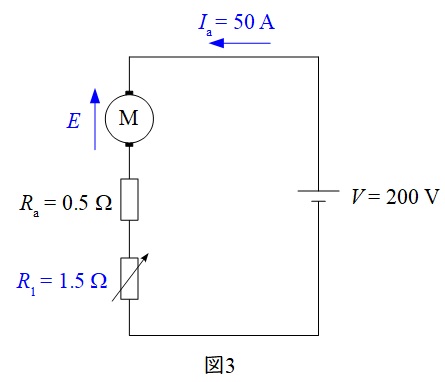
図3の回路方程式より逆起電力\(E\)を求めると,
\[
\begin{eqnarray}
V-E &=&\left( R_{\mathrm {a}}+R_{1}\right) I_{\mathrm {a}} \\[ 5pt ]
200-E &=&\left( 0.5+1.5\right) \times 50 \\[ 5pt ]
E &=&100 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。この条件で,電機子電流\(I_{\mathrm {a}}\)を\( \ 100 \ \mathrm {A} \ \)に増やした後の回路図は図4となる。
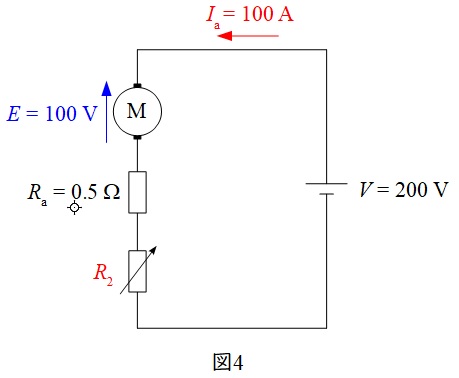
図4の回路方程式から可変抵抗\( \ R_{2} \ \)の値を求めると,
\[
\begin{eqnarray}
V-E &=&\left( R_{\mathrm {a}}+R_{2}\right) I_{\mathrm {a}} \\[ 5pt ]
200-100 &=&\left( 0.5+R_{2}\right) \times 100 \\[ 5pt ]
0.5+R_{2}&=&1 \\[ 5pt ]
R_{2} &=&0.5 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは