Contents
【問題】
【難易度】★★★☆☆(普通)
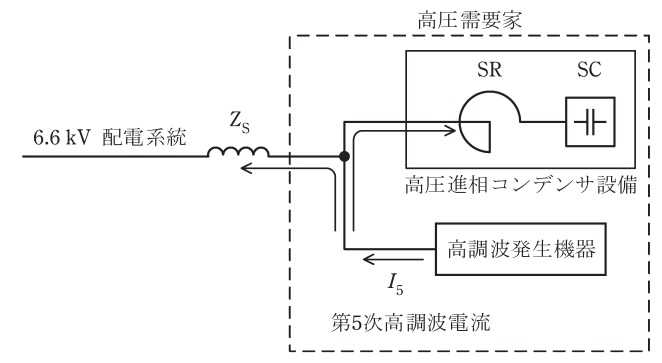
図に示すように,高調波発生機器と高圧進相コンデンサ設備を設置した高圧需要家が配電線インピーダンス\( \ \mathrm {Z}_{\mathrm {S}} \ \)を介して\( \ 6.6 \ \mathrm {kV} \ \)配電系統から受電しているとする。
コンデンサ設備は直列リアクトル\( \ \mathrm {SR} \ \)及びコンデンサ\( \ \mathrm {SC} \ \)で構成されているとし,高調波発生機器からは第\( \ 5 \ \)次高調波電流\( \ I_{\mathrm {5}} \ \)が発生するものとして,次の(a)及び(b)の問に答えよ。
ただし,\( \ \mathrm {Z}_{\mathrm {S}} \ \),\( \ \mathrm {SR} \ \),\( \ \mathrm {SC} \ \)の基本波周波数に対するそれぞれのインピーダンス\( \ {\dot Z}_{\mathrm {S1}} \ \),\( \ {\dot Z}_{\mathrm {SR1}} \ \),\( \ {\dot Z}_{\mathrm {SC1}} \ \)の値は次のとおりとする。
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {S1}}&=& \mathrm {j}4.4 \ \mathrm {\Omega },{\dot Z}_{\mathrm {SR1}}&=& \mathrm {j}33 \ \mathrm {\Omega },{\dot Z}_{\mathrm {SC1}}&=& -\mathrm {j}545 \ \mathrm {\Omega } \\[ 5pt ]
\end{eqnarray}
\]
(a) 系統に流出する高調波電流は高調波に対するコンデンサ設備インピーダンスと配電線インピーダンスの値により決まる。
\( \ \mathrm {Z}_{\mathrm {S}} \ \),\( \ \mathrm {SR} \ \),\( \ \mathrm {SC} \ \)の第\( \ 5 \ \)次高調波に対するそれぞれのインピーダンス\( \ {\dot Z}_{\mathrm {S5}} \ \),\( \ {\dot Z}_{\mathrm {SR5}} \ \),\( \ {\dot Z}_{\mathrm {SC5}} \ \)の値\( \ \mathrm {[\Omega ]} \ \)の組合せとして,最も近いものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{cccc}
& {\dot Z}_{\mathrm {S5}} & {\dot Z}_{\mathrm {SR5}} & {\dot Z}_{\mathrm {SC5}} \\
\hline
(1) & \mathrm {j}22 & \mathrm {j}165 & -\mathrm {j}2 \ 725 \\
\hline
(2) & \mathrm {j}9.8 & \mathrm {j}73.8 & -\mathrm {j}1 \ 218.7 \\
\hline
(3) & \mathrm {j}9.8 & \mathrm {j}73.8 & -\mathrm {j}243.7 \\
\hline
(4) & \mathrm {j}110 & \mathrm {j}825 & -\mathrm {j}21.8 \\
\hline
(5) & \mathrm {j}22 & \mathrm {j}165 & -\mathrm {j}109 \\
\hline
\end{array}
\]
(b) 「高圧又は特別高圧で受電する需要家の高調波抑制対策ガイドライン」では需要家から系統に流出する高調波電流の上限値が示されており,\( \ 6.6 \ \mathrm {kV} \ \)系統への第\( \ 5 \ \)次高調波の流出電流上限値は契約電力\( \ 1 \ \mathrm {kW} \ \)当たり\( \ 3.5 \ \mathrm {mA} \ \)となっている。
今,需要家の契約電力は\( \ 250 \ \mathrm {kW} \ \)とし,上記ガイドラインに従うものとする。
このとき,高調波発生機器から発生する第\( \ 5 \ \)次高調波電流\( \ I_{\mathrm {5}} \ \)の上限値(\( \ 6.6 \ \mathrm {kV} \ \)配電系統換算値)の値\( \ \mathrm {[A]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,高調波発生機器からの高調波は第\( \ 5 \ \)次高調波電流のみとし,その他の高調波及び記載以外のインピーダンスは無視するものとする。
なお,上記ガイドラインの実際の適用に当たっては,需要形態による適用緩和措置,高調波発生機器の種類,稼働率などを考慮する必要があるが,ここではこれらは考慮せず流出電流上限値のみを適用するものとする。
(1) \( \ 0.6 \ \) (2) \( \ 0.8 \ \) (3) \( \ 1.0 \ \) (4) \( \ 1.2 \ \) (5) \( \ 2.2 \ \)
【ワンポイント解説】
半分以上は理論と電力の計算問題ですが,例年の最終問題と比較すると,比較的取り組みやすい問題であったと思います。
法規では電力科目をはじめとする他の科目を含んだ総合問題も出題されるので,電力を科目合格していても電気施設管理の該当範囲は勉強していくようにして下さい。
1.コイル,コンデンサのリアクタンス(理論及び電力科目)
コイル\( \ L \ \mathrm {[H]} \ \),コンデンサ\( \ C \ \mathrm {[F]} \ \)があり,電源周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき,それぞれのリアクタンス\( \ X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)及び\( \ X_{\mathrm {C}} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {L}}&=&\mathrm {j}\omega L \\[ 5pt ]
&=&\mathrm {j}2\pi f L \\[ 5pt ]
-\mathrm {j}X_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C} \\[ 5pt ]
&=&\frac {1}{\mathrm {j}2\pi f C}\left( \frac {1}{\mathrm {j}}=\frac {1}{\mathrm {j}}\times \frac {\mathrm {j}}{\mathrm {j}}=-\mathrm {j}\right) \\[ 5pt ]
\end{eqnarray}
\]
で求められます。したがって,第\( \ 5 \ \)次高調波に対するリアクタンス\( \ X_{\mathrm {L5}} \ \mathrm {[\Omega ]} \ \)及び\( \ X_{\mathrm {C5}} \ \mathrm {[\Omega ]} \ \)は,周波数が\( \ 5 \ \)倍となるので,
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {L5}}&=&\mathrm {j}2\pi \times 5f \times L \\[ 5pt ]
&=&\mathrm {j}5 X_{\mathrm {L}} \\[ 5pt ]
-\mathrm {j}X_{\mathrm {C5}}&=&\frac {1}{\mathrm {j}2\pi \times 5f \times C} \\[ 5pt ]
&=&-\mathrm {j}\frac {X_{\mathrm {C}}}{5} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.分圧・分流の法則(理論科目)
①分圧の法則
図1に示した直列回路において,各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ]
V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ]
\end{eqnarray}
\]

②分流の法則
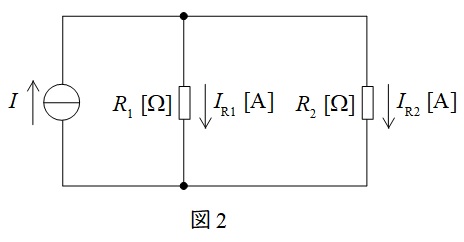
図2に示した並列回路において,各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ]
I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(a)解答:(5)
ワンポイント解説「1.コイル,コンデンサのリアクタンス」の通り,第\( \ 5 \ \)次高調波において,コイルのインピーダンスは基本波の\( \ 5 \ \)倍,コンデンサのインピーダンスは基本波の\( \ \displaystyle \frac {1}{5} \ \)倍であるから,\( \ {\dot Z}_{\mathrm {S5}} \ \),\( \ {\dot Z}_{\mathrm {SR5}} \ \),\( \ {\dot Z}_{\mathrm {SC5}} \ \)はそれぞれ,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {S5}}&=&5{\dot Z}_{\mathrm {S1}} \\[ 5pt ]
&=&5\times \mathrm {j}4.4 \\[ 5pt ]
&=&\mathrm {j}22 \ \mathrm {[\Omega ]} \\[ 5pt ]
{\dot Z}_{\mathrm {SR5}}&=&5{\dot Z}_{\mathrm {SR1}} \\[ 5pt ]
&=&5\times \mathrm {j}33 \\[ 5pt ]
&=&\mathrm {j}165 \ \mathrm {[\Omega ]} \\[ 5pt ]
{\dot Z}_{\mathrm {SC5}}&=&\frac {1}{5}{\dot Z}_{\mathrm {SC1}} \\[ 5pt ]
&=&\frac {1}{5}\times \left( -\mathrm {j}545 \right) \\[ 5pt ]
&=&-\mathrm {j}109 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(4)
題意より,需要家の契約電力は\( \ 250 \ \mathrm {kW} \ \)であり,\( \ 6.6 \ \mathrm {kV} \ \)配電系統への第\( \ 5 \ \)次高調波電流の流出電流上限値は契約電力\( \ 1 \ \mathrm {kW} \ \)当たり\( \ 3.5 \ \mathrm {mA} \ \)であるから,本問の高調波発生機器から流出可能な電流上限値\( \ I_{\mathrm {m5}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {m5}}&=&3.5\times 10^{-3}\times 250 \\[ 5pt ]
&=&0.875 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。
高調波発生機器からみた\( \ 6.6 \ \mathrm {kV} \ \)配電系統と高圧進相コンデンサ設備は並列であるから,ワンポイント解説「2.分圧・分流の法則(理論科目)」より,分流の法則を適用すると,
\[
\begin{eqnarray}
I_{\mathrm {m5}}&=&\frac {{\dot Z}_{\mathrm {SR5}}+{\dot Z}_{\mathrm {SC5}}}{{\dot Z}_{\mathrm {S5}}+{\dot Z}_{\mathrm {SR5}}+{\dot Z}_{\mathrm {SC5}}}I_{\mathrm {5}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,これを整理し,第\( \ 5 \ \)次高調波電流\( \ I_{\mathrm {5}} \ \)の上限値を求めると,
\[
\begin{eqnarray}
I_{\mathrm {5}}&=&\frac {{\dot Z}_{\mathrm {S5}}+{\dot Z}_{\mathrm {SR5}}+{\dot Z}_{\mathrm {SC5}}}{{\dot Z}_{\mathrm {SR5}}+{\dot Z}_{\mathrm {SC5}}}I_{\mathrm {m5}} \\[ 5pt ]
&=&\frac {\mathrm {j}22+\mathrm {j}165-\mathrm {j}109}{\mathrm {j}165-\mathrm {j}109}\times 0.875 \\[ 5pt ]
&=&\frac {78}{56}\times 0.875 \\[ 5pt ]
&≒&1.22 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは