《法規》〈電気施設管理〉[R4上:問13]調整池式水力発電所の貯水量及び発電電力に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

有効落差\( \ 80 \ \mathrm {m} \ \)の調整池式水力発電所がある。調整池に取水する自然流量は\( \ 10 \ \mathrm {m^{3}／s} \ \)一定であるとし，図のように\( \ 1 \ \)日のうち\( \ 12 \ \)時間は発電せずに自然流量の全量を貯水する。残り\( \ 12 \ \)時間のうち\( \ 2 \ \)時間は自然流量と同じ\( \ 10 \ \mathrm {m^{3}／s} \ \)の使用水量で発電を行い，他の\( \ 10 \ \)時間は自然流量より多い\( \ Q_{\mathrm {p}} \ \mathrm {[m^{3}／s]} \ \)の使用水量で発電して貯水分全量を使い切るものとする。このとき，次の(a)及び(b)の問に答えよ。

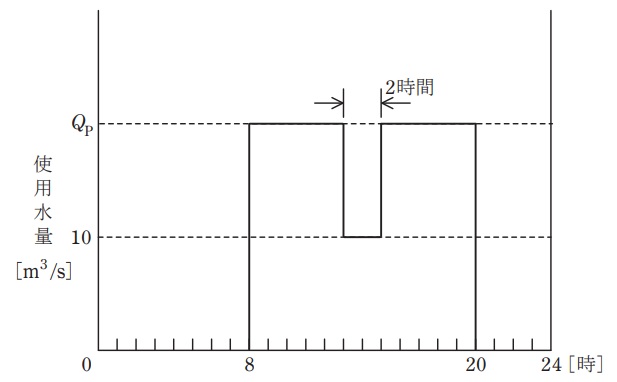
(a)　運用に最低限必要な有効貯水量の値\( \ \mathrm {[m^{3}]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 220\times 10^{3} \ \)　　(2)　\( \ 240\times 10^{3} \ \)　　(3)　\( \ 432\times 10^{3} \ \)　　(4)　\( \ 792\times 10^{3} \ \)
　(5)　\( \ 864\times 10^{3} \ \)

(b)　使用水量\( \ Q_{\mathrm {P}} \ \mathrm {[m^{3}／s]} \ \)で運転しているときの発電機出力の値\( \ \mathrm {[kW]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。ただし，運転中の有効落差は変わらず，水車効率，発電機効率はそれぞれ\( \ 90 \ \mathrm {％} \ \)，\( \ 95 \ \mathrm {％} \ \)で一定とし，溢水（いっすい）はないものとする。

　(1)　\( \ 12 \ 400 \ \)　　(2)　\( \ 14 \ 700 \ \)　　(3)　\( \ 16 \ 600 \ \)　　(4)　\( \ 18 \ 800 \ \)
　(5)　\( \ 20 \ 400 \ \)

【ワンポイント解説】

調整池式水力発電所の有効貯水量及び運転時の発電電力に関する問題です。
最低限の有効貯水量は最も貯水量が多い時間（\( \ 8 \ \)時）と最も貯水量が少ない時間（\( \ 20 \ \)時）との差となりますが，実際には\( \ 20 \ \)時に水位ゼロではいけないですし，\( \ 8 \ \)時に満水ギリギリではいけません。また，河川流量も一定ではないので，もう少し余裕を持った運用を行う必要があります。

1.水力発電所の出力\( \ P \ \mathrm {[kW]} \ \)
水力発電所の使用水量を\( \ Q \ \left[ \mathrm {m^{3}／s} \right] \)，有効落差を\( \ H \ \left[ \mathrm {m} \right] \ \)，水車効率を\( \ \eta _{\mathrm {w}}\)，発電機効率を\( \ \eta _{\mathrm {g}} \ \)とすると，水力発電所の出力\( \ P \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P&=&9.8QH\eta _{\mathrm {w}} \eta _{\mathrm {g}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(3)
必要な有効貯水量\( \ V \ \mathrm {[m^{3}]} \ \)は\( \ 20 \ \)時から\( \ 8 \ \)時までの\( \ 12 \ \)時間で貯水される水の量であり，自然流量は\( \ 10 \ \mathrm {m^{3}／s} \ \)であるから，
\[
\begin{eqnarray}
V&=&10\times 3 \ 600\times 12 \\[ 5pt ] &=&432 \ 000　→　432\times 10^{3} \ \mathrm {[m^{3}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(2)
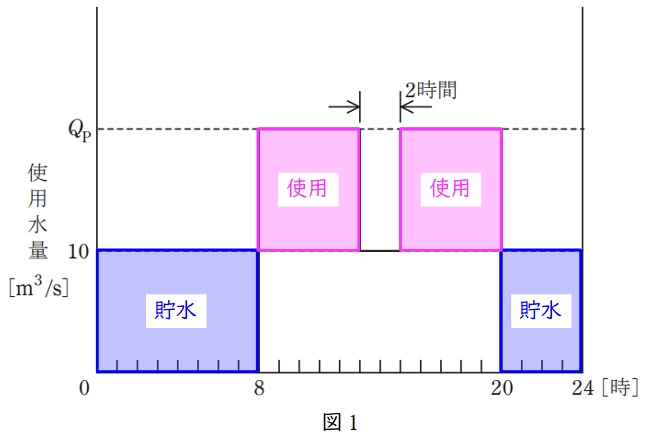
自然流量は\( \ 10 \ \mathrm {m^{3}／s} \ \)一定であるため，図1に示すように\( \ 20 \ \)時から\( \ 8 \ \)時までの\( \ 12 \ \)時間で貯水される水の量と\( \ 8 \ \)時から\( \ 13 \ \)時及び\( \ 15 \ \)時から\( \ 20 \ \)時の間の\( \ 10 \ \)時間で使用される水の量\( \ Q_{\mathrm {P}} \ \mathrm {[m^{3}／s]} \ \)と\( \ 10 \ \mathrm {m^{3}／s} \ \)の差分の合計は等しい。したがって，
\[
\begin{eqnarray}
\left( Q_{\mathrm {P}}-10\right) \times 3 \ 600\times 10&=&10\times 3 \ 600\times 12 \\[ 5pt ] Q_{\mathrm {P}}-10&=&12 \\[ 5pt ] Q_{\mathrm {P}}&=&22 \ \mathrm {[m^{3}／s]} \\[ 5pt ] \end{eqnarray}
\] となるから，このときの発電機出力\( \ P_{\mathrm {P}} \ \mathrm {[kW]} \ \)は，ワンポイント解説「1.水力発電所の出力\( \ P \ \mathrm {[kW]} \ \)」の通り，
\[
\begin{eqnarray}
P_{\mathrm {P}}&=&9.8Q_{\mathrm {P}}H\eta _{\mathrm {w}} \eta _{\mathrm {g}} \\[ 5pt ] &=&9.8\times 22\times 80 \times 0.90\times 0.95 \\[ 5pt ] &≒&14 \ 700 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。