《機械》〈照明〉[H22:問17]異なる２個の光源を使用したときの水平面照度に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

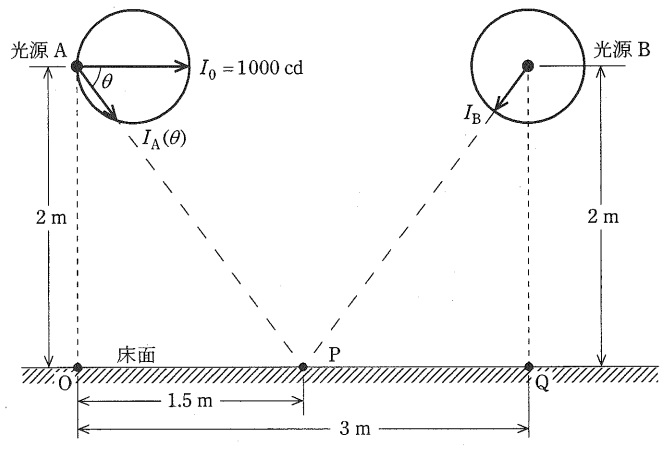
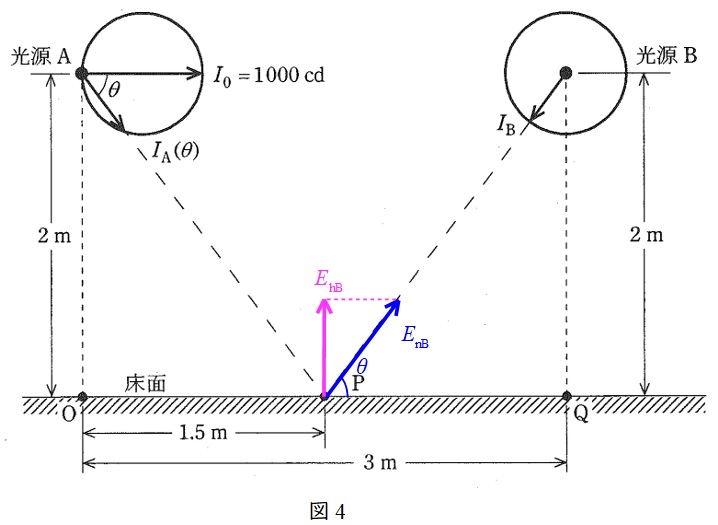
図に示すように，床面上の直線距離\( \ 3 \ \mathrm {[m]} \ \)離れた点\( \ \mathrm {O} \ \)及び点\( \ \mathrm {Q} \ \)それぞれの真上\( \ 2 \ \mathrm {[m]} \ \)のところに，配光特性の異なる\( \ 2 \ \)個の光源\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)をそれぞれ取り付けたとき，\( \ \overline {\mathrm {OQ}} \ \)線上の中点\( \ \mathrm {P} \ \)の水平面照度に関して，次の(a)及び(b)に答えよ。

ただし，光源\( \ \mathrm {A} \ \)は床面に対し平行な方向に最大光度\( \ I_{0} \ \mathrm {[cd]} \ \)で，この\( \ I_{0} \ \)の方向と角\( \ \theta \ \)をなす方向に\( \ I_{\mathrm {A}}\left( \theta \right) =1 \ 000 \cos \theta \ \mathrm {[cd]} \ \)の配光をもつ。光源\( \ \mathrm {B} \ \)は全光束\( \ 5 \ 000 \ \mathrm {[lm]} \ \)で，どの方向にも光度が等しい均等放射光源である。

(a)　まず，光源\( \ \mathrm {A} \ \)だけを点灯したとき，点\( \ \mathrm {P} \ \)の水平面照度\( \ \mathrm {[lx]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 57.6 \ \)　　(2)　\( \ 76.8 \ \)　　(3)　\( \ 96.0 \ \)　　(4)　\( \ 102 \ \)　　(5)　\( \ 192 \ \)

(b)　次に，光源\( \ \mathrm {A} \ \)と光源\( \ \mathrm {B} \ \)の両方を点灯したとき，点\( \ \mathrm {P} \ \)の水平面照度\( \ \mathrm {[lx]} \ \)の値として，最も近いのは次のうちどれか。

　(1)　\( \ 128 \ \)　　(2)　\( \ 141 \ \)　　(3)　\( \ 160 \ \)　　(4)　\( \ 172 \ \)　　(5)　\( \ 256 \ \)

【ワンポイント解説】

照度の異なる２つの光源を使用したときの水平面照度を求める問題です。
照明の問題としては最も出題されやすいパターンの問題で平成30年問17にも類題が出題されています。
水平面照度の考え方は必ず理解しておくようにしましょう。

1.立体角の定義
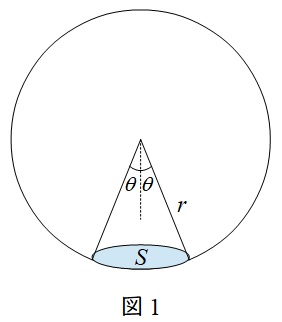
図1のように球体があり，半径\( \ r \ \mathrm {[m]} \ \)の錐体が球面を切り取った時の面積を\( \ S \ \mathrm {[m^{2}]} \ \)とすると，立体角\( \ \omega \ \mathrm {[sr]} \ \)は，
\[
\begin{eqnarray}
\omega &=&\frac {S}{r^{2}} \\[ 5pt ] \end{eqnarray}
\] であり，平面角\( \ \theta \ \mathrm {[rad]} \ \)で表すと，
\[
\begin{eqnarray}
\omega &=&2\pi \left( 1-\cos \theta \right) \\[ 5pt ] \end{eqnarray}
\] となります。球全体の立体角は\( \ \theta = \pi \ \)の時であり，\( \ \omega =4\pi \ \)となります。

2.光度\( \ I \ \)
ある方向に向かう光束\( \ F \ \mathrm {[lm]} \ \)を立体角\( \ \omega \ \mathrm {[sr]} \ \)で割ったものが光度\( \ I \ \mathrm {[cd]} \ \)となります。
\[
\begin{eqnarray}
I &=&\frac {\Delta F}{\Delta \omega } \\[ 5pt ] \end{eqnarray}
\]

3.水平面照度\( \ E_{\mathrm {h}} \ \)
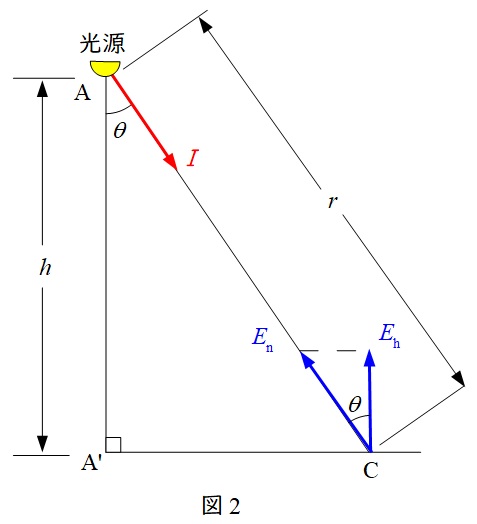
図2のように，点光源から光度\( \ I \ \mathrm {[cd]} \ \)で\( \ \mathrm {C} \ \)点に向かって光が照射されているとき，法線照度\( \ E_{\mathrm {n}} \ \mathrm {[lx]} \ \)は，
\[
\begin{eqnarray}
E_{\mathrm {n}} &=&\frac {I}{r^{2}} \\[ 5pt ] \end{eqnarray}
\] で求められ，水平面照度\( \ E_{\mathrm {h}} \ \mathrm {[lx]} \ \)は，\( \ E_{\mathrm {n}} \ \mathrm {[lx]} \ \)の余弦\( \ \cos \theta \ \)であるから，
\[
\begin{eqnarray}
E_{\mathrm {h}} &=&E_{\mathrm {n}}\cos \theta \\[ 5pt ] &=&\frac {I}{r^{2}}\cdot \frac {h}{r} \\[ 5pt ] &=&\frac {hI}{r^{3}}
\end{eqnarray}
\] となります。

【解答】

(a)解答：(2)
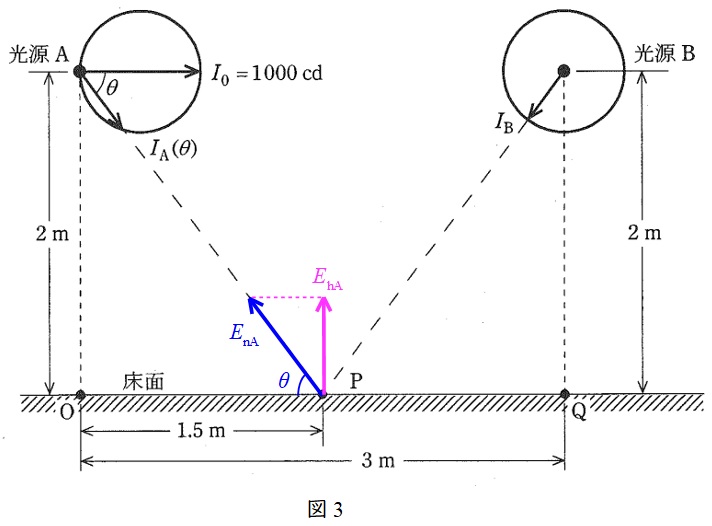
図3のように光源\( \ \mathrm {A} \ \)による点\( \ \mathrm {P} \ \)の法線照度及び水平面照度を\( \ E_{\mathrm {nA}} \ \mathrm {[lx]} \ \)及び\( \ E_{\mathrm {hA}} \ \mathrm {[lx]} \ \)とする。
光源\( \ \mathrm {A} \ \)から点\( \ \mathrm {P} \ \)までの距離\( \ l \ \mathrm {[m]} \ \)は，
\[
\begin{eqnarray}
l &=&\sqrt {1.5^{2}+2.0^{2}} \\[ 5pt ] &=&2.5 \ \mathrm {[m]} \\[ 5pt ] \end{eqnarray}
\] であることから，\( \ I_{\mathrm {A}}\left( \theta \right) \ \mathrm {[cd]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {A}}\left( \theta \right) &=&1 \ 000 \cos \theta \\[ 5pt ] &=&1 \ 000 \times \frac {1.5}{l} \\[ 5pt ] &=&1 \ 000 \times \frac {1.5}{2.5} \\[ 5pt ] &=&600 \ \mathrm {[cd]} \\[ 5pt ] \end{eqnarray}
\] なる。よって，点\( \ \mathrm {P} \ \)の法線照度\( \ E_{\mathrm {nA}} \ \mathrm {[lx]} \ \)は，ワンポイント解説「3.水平面照度\( \ E_{\mathrm {h}} \ \)」の通り，
\[
\begin{eqnarray}
E_{\mathrm {nA}} &=&\frac {I_{\mathrm {A}}\left( \theta \right)}{l^{2}} \\[ 5pt ] &=&\frac {600}{2.5^{2}} \\[ 5pt ] &=&96 \ \mathrm {[lx]} \\[ 5pt ] \end{eqnarray}
\] となり，水平面照度\( \ E_{\mathrm {hA}} \ \mathrm {[lx]} \ \)は\( \ \theta \ \)の位置に注意すると，
\[
\begin{eqnarray}
E_{\mathrm {hA}} &=&E_{\mathrm {nA}}\sin \theta \\[ 5pt ] &=&96\times \frac {2}{l} \\[ 5pt ] &=&96\times \frac {2}{2.5} \\[ 5pt ] &=&76.8 \ \mathrm {[lx]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(1)
図4のように光源\( \ \mathrm {B} \ \)による点\( \ \mathrm {P} \ \)の法線照度及び水平面照度を\( \ E_{\mathrm {nB}} \ \mathrm {[lx]} \ \)及び\( \ E_{\mathrm {hB}} \ \mathrm {[lx]} \ \)とする。
光源\( \ \mathrm {B} \ \)による点\( \ \mathrm {P} \ \)の方向への光度\( \ I_{\mathrm {B}} \ \mathrm {[cd]} \ \)は，どの方向にも光度が等しい均等放射光源であることから，ワンポイント解説「2.光度\( \ I \ \)」の通り，
\[
\begin{eqnarray}
I_{\mathrm {B}} &=&\frac {F}{\omega } \\[ 5pt ] &=&\frac {5 \ 000}{4\pi } \\[ 5pt ] &≒&397.9 \ \mathrm {[cd]} \\[ 5pt ] \end{eqnarray}
\] となる。これより，光源\( \ \mathrm {B} \ \)による点\( \ \mathrm {P} \ \)の法線照度\( \ E_{\mathrm {nB}} \ \mathrm {[lx]} \ \)は，ワンポイント解説「3.水平面照度\( \ E_{\mathrm {h}} \ \)」の通り，
\[
\begin{eqnarray}
E_{\mathrm {nB}} &=&\frac {I_{\mathrm {B}}}{l^{2}} \\[ 5pt ] &=&\frac {397.9}{2.5^{2}} \\[ 5pt ] &≒&63.66 \ \mathrm {[lx]} \\[ 5pt ] \end{eqnarray}
\] となり，水平面照度\( \ E_{\mathrm {hB}} \ \mathrm {[lx]} \ \)は\( \ \theta \ \)の位置に注意すると，
\[
\begin{eqnarray}
E_{\mathrm {hB}} &=&E_{\mathrm {nB}}\sin \theta \\[ 5pt ] &=&63.66\times \frac {2}{l} \\[ 5pt ] &=&63.66\times \frac {2}{2.5} \\[ 5pt ] &≒&50.93 \ \mathrm {[lx]} \\[ 5pt ] \end{eqnarray}
\] と求められる。以上から，全体の水平面照度は，
\[
\begin{eqnarray}
E_{\mathrm {hA}}+E_{\mathrm {hB}} &=&76.8+50.93 \\[ 5pt ] &≒&128 \ \mathrm {[lx]} \\[ 5pt ] \end{eqnarray}
\] と求められる。