《機械》〈回転機〉[H22:問2]直流分巻発電機の固定損の導出に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

直流発電機の損失は，固定損，直接負荷損，界磁回路損及び漂遊負荷損に分類される。

定格出力\( \ 50 \ \mathrm {[kW]} \ \)，定格電圧\( \ 200 \ \mathrm {[V]} \ \)の直流分巻発電機がある。この発電機の定格負荷時の効率は\( \ 94 \ \mathrm {[％]} \ \)である。このときの発電機の固定損\( \ \mathrm {[kW]} \ \)の値として，最も近いのは次のうちどれか。

ただし，ブラシの電圧降下と漂遊負荷損は無視するものとする。また，電機子回路及び界磁回路の抵抗はそれぞれ\( \ 0.03 \ \mathrm {[\Omega ]} \ \)及び\( \ 200 \ \mathrm {[\Omega ]} \ \)とする。

　(1)　\( \ 1.10 \ \)　　(2)　\( \ 1.12 \ \)　　(3)　\( \ 1.13 \ \)　　(4)　\( \ 1.30 \ \)　　(5)　\( \ 1.32 \ \)　　

【ワンポイント解説】

直流分巻発電機の損失に関する問題です。
導出過程が思いつけばそれほど難解ではありませんが，おそらくこの問題文のみだと導出方法がピンとくる受験生の方が少ないかなと予想されます。
解いていくうちにだんだん見えてくるものもあると思いますので，まずは等価回路を描き，与えられている値を等価回路に当てはめて考えてみるようにして下さい。

1.分巻発電機及び電動機の等価回路と特性
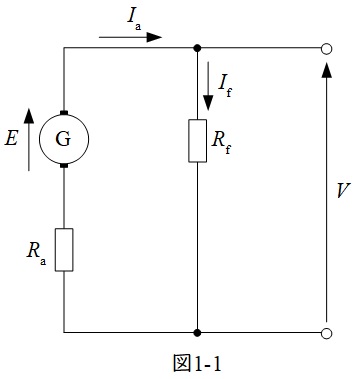
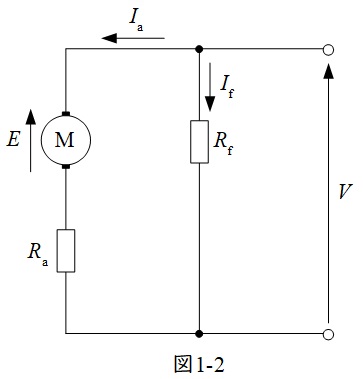
分巻発電機の等価回路を図1-1，分巻電動機の等価回路を図1-2に示します。ただし，図において，\( \ E \ \)は誘導起電力(電動機の場合は逆起電力)，\( \ V \ \)は端子電圧，\( \ I_{\mathrm {a}} \ \)は電機子電流，\( \ I_{\mathrm {f}} \ \)は界磁電流，\( \ R_{\mathrm {a}} \ \)は電機子抵抗，\( \ R_{\mathrm {f}} \ \)は界磁抵抗です。
図を見て分かる通り，発電機も電動機もほぼ同じ等価回路となります。
磁束を\( \ \phi \ \)，回転速度を\( \ N \ \)とすると，\( \ \phi ∝ I_{\mathrm {f}} \ \)となるので，誘導起電力(逆起電力)\( \ E \ \)は，
\[
\begin{eqnarray}
E &=&k_{\mathrm {e}}\phi N \\[ 5pt ] &=&k_{\mathrm {e}}^{\prime } I_{\mathrm {f}} N \\[ 5pt ] \end{eqnarray}
\] となります。またトルク\( \ T \ \)は，
\[
\begin{eqnarray}
T &=&k_{\mathrm {f}}\phi I_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.直巻発電機及び電動機の等価回路と特性
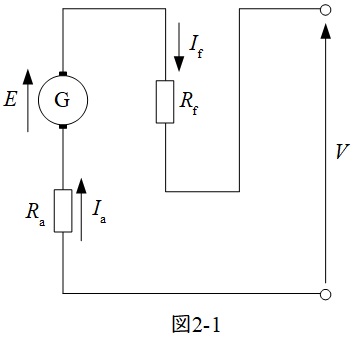
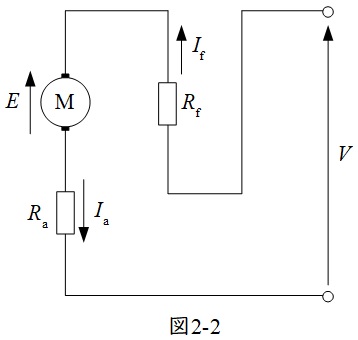
直巻発電機の等価回路を図2-1，直巻電動機の等価回路を図2-2に示します。分巻発電機の時と同様に，\( \ E \ \)は誘導起電力(電動機の場合は逆起電力)，\( \ V \ \)は端子電圧，\( \ I_{\mathrm {a}} \ \)は電機子電流，\( \ I_{\mathrm {f}} \ \)は界磁電流，\( \ R_{\mathrm {a}} \ \)は電機子抵抗，\( \ R_{\mathrm {f}} \ \)は界磁抵抗です。
一番の特徴は分巻は電機子回路と界磁回路が並列なのに対し，直巻は直列であるということです。
磁束を\( \ \phi \ \)，回転速度を\( \ N \ \)とすると，\( \ \phi ∝ I_{\mathrm {f}}=I_{\mathrm {a}} \ \)となるので，誘導起電力(逆起電力)\( \ E \ \)は，
\[
\begin{eqnarray}
E &=&k_{\mathrm {e}}\phi N \\[ 5pt ] &=&k_{\mathrm {e}}^{\prime } I_{\mathrm {f}} N \\[ 5pt ] &=&k_{\mathrm {e}}^{\prime } I_{\mathrm {a}} N \\[ 5pt ] \end{eqnarray}
\] となります。またトルク\( \ T \ \)は，
\[
\begin{eqnarray}
T &=&k_{\mathrm {f}}\phi I_{\mathrm {a}} \\[ 5pt ] &=&k_{\mathrm {f}}^{\prime } I_{\mathrm {a}}^{2} \\[ 5pt ] \end{eqnarray}
\] となり，トルクが電機子電流の\( \ 2 \ \)乗に比例するという特徴があります。

3.直流発電機の効率
直流発電機の\( \ \eta \ \mathrm {[％]} \ \)は，出力\( \ P \ \mathrm {[W]} \ \)，固定損（鉄損と機械損の合計）\( \ P_{\mathrm {i}} \ \mathrm {[W]} \ \)，直接負荷損\( \ P_{\mathrm {a}} \ \mathrm {[W]} \ \)，界磁回路損\( \ P_{\mathrm {f}} \ \mathrm {[W]} \ \)とし，ブラシの損失や漂遊負荷損を無視すると，
\[
\begin{eqnarray}
\eta &=&\frac {出力}{入力}\times 100 \\[ 5pt ] &=&\frac {出力}{出力+損失}\times 100 \\[ 5pt ] &=&\frac {P}{P+P_{\mathrm {i}}+P_{\mathrm {a}}+P_{\mathrm {f}}}\times 100 \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

解答：(1)
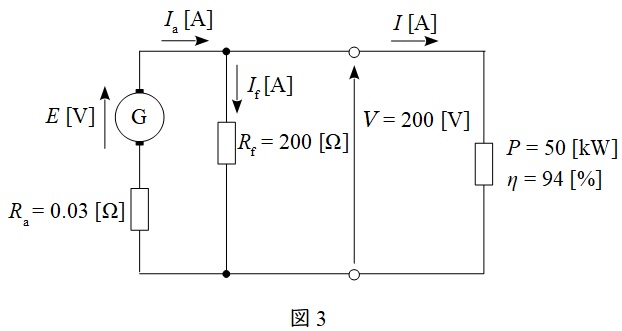
題意に沿って等価回路を描くと図3のようになる。
図3において，負荷電流\( \ I \ \mathrm {[A]} \ \)の大きさは，
\[
\begin{eqnarray}
P &=&VI \\[ 5pt ] I&=&\frac {P}{V} \\[ 5pt ] &=&\frac {50\times 10^{3}}{200} \\[ 5pt ] &=&250 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であり，界磁電流\( \ I_{\mathrm {f}} \ \mathrm {[A]} \ \)の大きさは，
\[
\begin{eqnarray}
I_{\mathrm {f}} &=&\frac {V}{R_{\mathrm {f}}} \\[ 5pt ] &=&\frac {200}{200} \\[ 5pt ] &=&1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であるため，電機子電流\( \ I_{\mathrm {a}} \ \mathrm {[A]} \ \)の大きさは，
\[
\begin{eqnarray}
I_{\mathrm {a}} &=&I+I_{\mathrm {f}} \\[ 5pt ] &=&250+1 \\[ 5pt ] &=&251 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，界磁回路損\( \ P_{\mathrm {f}} \ \mathrm {[W]} \ \)及び直接負荷損\( \ P_{\mathrm {a}} \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {f}} &=&R_{\mathrm {f}}I_{\mathrm {f}}^{2} \\[ 5pt ] &=&200\times 1^{2} \\[ 5pt ] &=&200 \ \mathrm {[W]} \\[ 5pt ] P_{\mathrm {a}} &=&R_{\mathrm {a}}I_{\mathrm {a}}^{2} \\[ 5pt ] &=&0.03\times 251^{2} \\[ 5pt ] &≒&1 \ 890 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] であるから，ワンポイント解説「3.直流発電機の効率」より固定損\( \ P_{\mathrm {i}} \ \mathrm {[W]} \ \)を求めると，
\[
\begin{eqnarray}
\eta &=&\frac {P}{P+P_{\mathrm {i}}+P_{\mathrm {a}}+P_{\mathrm {f}}}\times 100 \\[ 5pt ] 94&=&\frac {50\times 10^{3}}{50\times 10^{3}+P_{\mathrm {i}}+1 \ 890+200}\times 100 \\[ 5pt ] 94&=&\frac {50 \ 000}{P_{\mathrm {i}}+52 \ 090}\times 100 \\[ 5pt ] P_{\mathrm {i}}+52 \ 090&=&\frac {50 \ 000\times 100}{94} \\[ 5pt ] P_{\mathrm {i}}&=&\frac {50 \ 000\times 100}{94}-52 \ 090 \\[ 5pt ] &≒&1 \ 100 \ \mathrm {[W]}　→　1.10 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。