《機械》〈回転機〉[H23:問16]他励直流電動機の速度制御に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

負荷に直結された他励直流電動機を，電機子電圧を変化させることによって速度制御することを考える。

電機子抵抗が\( \ 0.4 \ \mathrm {[\Omega ]} \ \)，界磁磁束は界磁電流に比例するものとして，次の(a)及び(b)の問に答えよ。

(a)　界磁電流を\( \ I_{\mathrm {f1}} \ \mathrm {[A]} \ \)とし，電動機が\( \ 600 \ \mathrm {[min^{-1}]} \ \)で回転しているときの誘導起電力は\( \ 200 \ \mathrm {[V]} \ \)であった。このとき電機子電流が\( \ 20 \ \mathrm {[A]} \ \)一定で負荷と釣り合った状態にするには，電機子電圧を何\( \ \mathrm {[V]} \ \)に制御しなければならないか，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 8 \ \)　　(2)　\( \ 80 \ \)　　(3)　\( \ 192 \ \)　　(4)　\( \ 200 \ \)　　(5)　\( \ 208 \ \)

(b)　負荷は，トルクが一定で回転速度に対して機械出力が比例して上昇する特性であるとして，磁気飽和，電機子反作用，機械系の損失などは無視できるものとする。

電動機の回転速度を\( \ 1 \ 320 \ \mathrm {[min^{-1}]} \ \)にしたときに，界磁電流を\( \ I_{\mathrm {f1}} \ \mathrm {[A]} \ \)の\( \ \displaystyle \frac {1}{2} \ \)にして，電機子電流がある一定の値で負荷と釣り合った状態にするには，電機子電圧を何\( \ \mathrm {[V]} \ \)に制御しなければならないか，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 216 \ \)　　(2)　\( \ 228 \ \)　　(3)　\( \ 236 \ \)　　(4)　\( \ 448 \ \)　　(5)　\( \ 456 \ \)

【ワンポイント解説】

直流電動機の特性に関する問題です。
(b)はしっかりと特性を理解していないと解けない問題ですが，(a)は等価回路が描ければ解ける問題です。
合格するためには(b)を理解することも大事ですが，それ以上に(a)を確実に得点することが重要となります。

1.直流他励電動機の等価回路
図1に直流他励電動機の等価回路を示します。図1において，\( \ V \ \)は端子電圧，\( \ E \ \)は逆起電力，\( \ V_{\mathrm {f}} \ \)は界磁電圧，\( \ I_{\mathrm {a}} \ \)は電機子電流，\( \ I_{\mathrm {f}} \ \)は界磁電流，\( \ R_{\mathrm {a}} \ \)は電機子抵抗，\( \ R_{\mathrm {f}} \ \)は界磁抵抗となります。
他励式の特徴としては，界磁回路が独立しているので，界磁磁束を独立して制御できるという特徴があります。

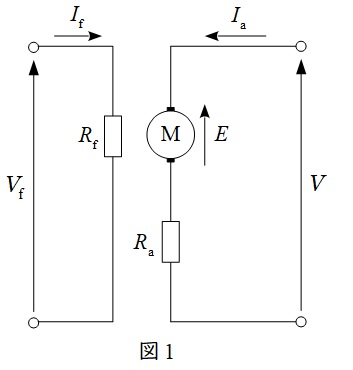
また，上記の等価回路にキルヒホッフの法則を適用すると，以下の関係式が導き出せることが分かります。
\[
\begin{eqnarray}
V &=& E+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] I_{\mathrm {f}} &=& \frac {E_{\mathrm {f}}}{R_{\mathrm {f}}} \\[ 5pt ] \end{eqnarray}
\]

2.直流機の誘導起電力(逆起電力)\( \ E \ \)
磁極の数\( \ p \ \)，電機子導体数\( \ Z \ \)，電機子巻線並列回路数\( \ a \ \)，各極の磁束\( \ \phi \ \)，回転速度\( \ N \ \)とすると，直流機の誘導起電力(逆起電力)\( \ E \ \)は，
\[
\begin{eqnarray}
E &=&\frac {pZ}{60a}\phi N \\[ 5pt ] &=&k_{\mathrm {e}}\phi N \\[ 5pt ] \end{eqnarray}
\] となり，磁束\( \ \phi \ \)と回転速度\( \ N \ \)に比例します。

3.直流機のトルク\( \ T \ \)
磁極の数\( \ p \ \)，電機子導体数\( \ Z \ \)，電機子巻線並列回路数\( \ a \ \)，各極の磁束\( \ \phi \ \)，電機子電流\( \ I_{\mathrm {a}} \ \)とすると，直流機のトルク\( \ T \ \)は，
\[
\begin{eqnarray}
T &=&\frac {pZ}{2\pi a}\phi I_{\mathrm {a}} \\[ 5pt ] &=&k_{\mathrm {f}}\phi I_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] となり，磁束\( \ \phi \ \)と電機子電流\( \ I_{\mathrm {a}} \ \)に比例します。

【解答】

(a)解答：(5)
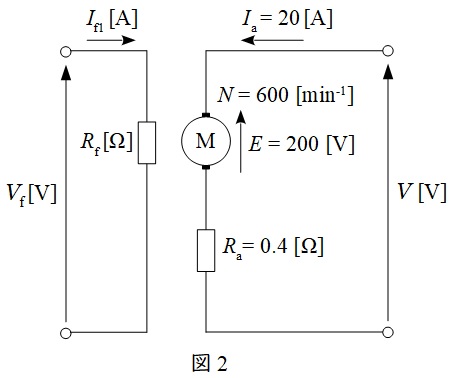
ワンポイント解説「1.直流他励電動機の等価回路」の通り，題意に沿って等価回路を描くと図2のようになる。
図2の等価回路の回路方程式から，
\[
\begin{eqnarray}
V &=&E+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] &=&200+0.4\times 20 \\[ 5pt ] &=&208 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
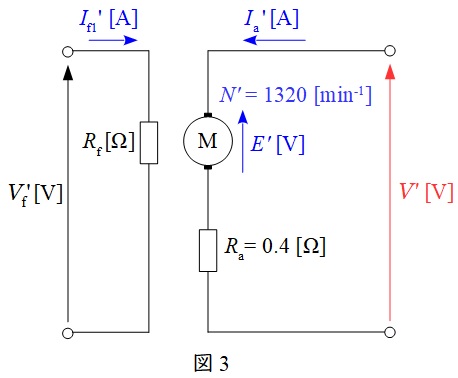
電動機が最終的に釣り合った状態の等価回路を図3に示す。
トルクが一定であるから，ワンポイント解説「3.直流機のトルク\( \ T \ \)」より，
\[
\begin{eqnarray}
T =k_{\mathrm {f}}\phi I_{\mathrm {a}}&=&k_{\mathrm {f}}\phi ^{\prime } I_{\mathrm {a}}^{\prime } \\[ 5pt ] \phi I_{\mathrm {a}}&=&\phi ^{\prime } I_{\mathrm {a}}^{\prime } \\[ 5pt ] \end{eqnarray}
\] となる。ここで，磁束\( \ \phi \ \)は界磁電流\( \ I_{\mathrm {f1}} \ \)に比例し，界磁電流\( \ I_{\mathrm {f1}}^{\prime } \ \)は\( \ I_{\mathrm {f1}} \ \)の\( \ \displaystyle \frac {1}{2} \ \)となるから，
\[
\begin{eqnarray}
I_{\mathrm {f1}} I_{\mathrm {a}}&=&I_{\mathrm {f1}}^{\prime } I_{\mathrm {a}}^{\prime } \\[ 5pt ] I_{\mathrm {f1}} I_{\mathrm {a}}&=&\frac {1}{2}I_{\mathrm {f1}} I_{\mathrm {a}}^{\prime } \\[ 5pt ] I_{\mathrm {a}}&=&\frac {1}{2} I_{\mathrm {a}}^{\prime } \\[ 5pt ] I_{\mathrm {a}}^{\prime }&=&2 I_{\mathrm {a}} \\[ 5pt ] &=&2 \times 20 \\[ 5pt ] &=&40 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。また，回転速度が\( \ N=600 \ \mathrm {[min^{-1}]} \ \)から\( \ N^{\prime }=1320 \ \mathrm {[min^{-1}]} \ \)に変化しているので，ワンポイント解説「2.直流機の誘導起電力(逆起電力)\( \ E \ \)」の通り，
\[
\begin{eqnarray}
E^{\prime }&=&k_{\mathrm {e}}\phi ^{\prime }N^{\prime } \\[ 5pt ] &=&k_{\mathrm {e}}\cdot \frac {1}{2}\phi \cdot \frac {1320}{600}N \\[ 5pt ] &=&\frac {1}{2}\times \frac {1320}{600}\cdot k_{\mathrm {e}}\phi N \\[ 5pt ] &=&1.1E \\[ 5pt ] &=&1.1\times 200 \\[ 5pt ] &=&220 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。以上から，図3の電機子回路における回路方程式より，
\[
\begin{eqnarray}
V^{\prime } &=&E^{\prime }+R_{\mathrm {a}}I_{\mathrm {a}}^{\prime } \\[ 5pt ] &=&220+0.4\times 40 \\[ 5pt ] &=&236 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。