《機械》〈変圧器〉[H23:問15]変圧器の百分率インピーダンス降下と電圧変動率に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次の定数をもつ定格一次電圧\( \ 2 \ 000 \ \mathrm {[V]} \ \)，定格二次電圧\( \ 100 \ \mathrm {[V]} \ \)，定格二次電流\( \ 1 \ 000 \ \mathrm {[A]} \ \)の単相変圧器について，(a)及び(b)の問に答えよ。

ただし，励磁アドミタンスは無視するものとする。

一次巻線抵抗\( \ r_{1}=0.2 \ \mathrm {[\Omega ]} \ \)，一次漏れリアクタンス\( \ x_{1}=0.6 \ \mathrm {[\Omega ]} \ \)，
二次巻線抵抗\( \ r_{2}=0.0005 \ \mathrm {[\Omega ]} \ \)，二次漏れリアクタンス\( \ x_{2}=0.0015 \ \mathrm {[\Omega ]} \ \)

(a)　この変圧器の百分率インピーダンス降下\( \ \mathrm {[％]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 2.00 \ \)　　(2)　\( \ 3.16 \ \)　　(3)　\( \ 4.00 \ \)　　(4)　\( \ 33.2 \ \)　　(5)　\( \ 664 \ \)

(b)　この変圧器の二次側に力率\( \ 0.8 \ \)（遅れ）の定格負荷を接続して運転しているときの電圧変動率\( \ \mathrm {[％]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 2.60 \ \)　　(2)　\( \ 3.00 \ \)　　(3)　\( \ 27.3 \ \)　　(4)　\( \ 31.5 \ \)　　(5)　\( \ 521 \ \)

【ワンポイント解説】

変圧器の百分率インピーダンス降下と電圧変動率に関する問題です。
一次二次の換算をし定格電流を求める問題は，変圧器の計算としては非常に出題されやすいパターンの問題です。
よく理解しておくようにしましょう。

1.変圧器の巻数比と変圧比，変流比の関係
変圧器の一次側の巻数\( \ N_{1} \ \)，電圧\( \ V_{1} \ \mathrm {[V]} \ \)，電流\( \ I_{1} \ \mathrm {[A]} \ \)，二次側の巻数\( \ N_{2} \ \)，電圧\( \ V_{2} \ \mathrm {[V]} \ \)，電流\( \ I_{2} \ \mathrm {[A]} \ \)とすると，巻数比\( \ \displaystyle a=\frac {N_{1}}{N_{2}} \ \)は，
\[
\begin{eqnarray}
a&=&\frac {N_{1}}{N_{2}} =\frac {V_{1}}{V_{2}}=\frac {I_{2}}{I_{1}} \\[ 5pt ] \end{eqnarray}
\] となります。インピーダンスは電圧を電流で割ったものであるため，一次側換算のインピーダンス\( \ Z_{1} \ \mathrm {[\Omega ]} \ \)，二次側換算のインピーダンス\( \ Z_{2} \ \mathrm {[\Omega ]} \ \)とすると，
\[
\begin{eqnarray}
\frac {Z_{1}}{Z_{2}} &=&\frac {\displaystyle \frac {V_{1}}{I_{1}}}{\displaystyle \frac {V_{2}}{I_{2}}} \\[ 5pt ] &=&\frac {V_{1}}{I_{1}}\times \frac {I_{2}}{V_{2}} \\[ 5pt ] &=&\frac {V_{1}}{V_{2}}\times \frac {I_{2}}{I_{1}} \\[ 5pt ] &=&\left( \frac {N_{1}}{N_{2}} \right) ^{2} \\[ 5pt ] &=&a^{2} \\[ 5pt ] \end{eqnarray}
\] となります。

2.電圧変動率の近似式
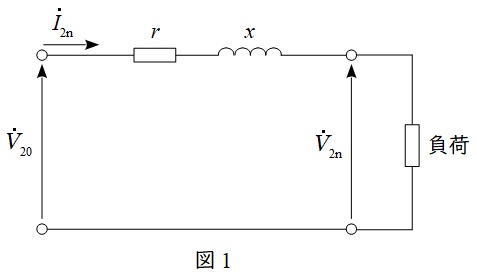
図1のように，変圧器を二次側に換算した回路（\( \ r \ \)は一次二次を合算した抵抗値，\( \ x \ \)は一次二次を合算したリアクタンス値）において，無負荷時の二次端子電圧を\( \ V_{20} \ \)，定格負荷時の二次端子電圧を\( \ V_{\mathrm {2n}} \ \)とすると，電圧変動率\( \ \varepsilon \ \)は，
\[
\begin{eqnarray}
\varepsilon &=&\frac {V_{20}-V_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \ [％] \\[ 5pt ] \end{eqnarray}
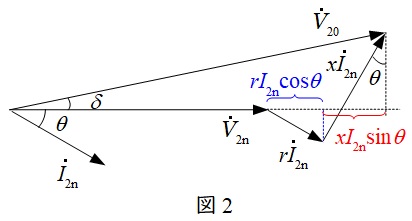
\] で定義されます。定格二次電流を\( \ I_{\mathrm {2n}} \ \)とするとベクトル図は図2の通りとなります。\( \ V_{20} \ \)と\( \ V_{\mathrm {2n}} \ \)の位相差\( \ \delta \ \)が十分に小さいとすると，
\[
\begin{eqnarray}
\varepsilon &=&\frac {V_{20}-V_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \\[ 5pt ] &≒&\frac {rI_{\mathrm {2n}}\cos \theta +xI_{\mathrm {2n}}\sin \theta }{V_{\mathrm {2n}}}\times 100 \\[ 5pt ] &=&\frac {rI_{\mathrm {2n}}}{V_{\mathrm {2n}}}\cos \theta \times 100 +\frac {xI_{\mathrm {2n}}}{V_{\mathrm {2n}}}\sin \theta \times 100 \\[ 5pt ] &=&p\cos \theta +q\sin \theta \\[ 5pt ] \end{eqnarray}
\] となります。上式に出てくる\( \ \displaystyle p=\frac {rI_{\mathrm {2n}}}{V_{\mathrm {2n}}} \times 100 \ \)は百分率抵抗降下，\( \ \displaystyle q=\frac {xI_{\mathrm {2n}}}{V_{\mathrm {2n}}} \times 100 \ \)は百分率リアクタンス降下と呼ばれます。

【解答】

(a)解答：(2)
定格一次電圧\( \ V_{1}=2 \ 000 \ \mathrm {[V]} \ \)，定格二次電圧\( \ V_{2}=100 \ \mathrm {[V]} \ \)なので，二次側に換算した一次巻線抵抗値\( \ r_{1}^{\prime } \ \mathrm {[\Omega ]} \ \)及び二次側に換算した一次漏れリアクタンス値\( \ x_{1}^{\prime } \ \mathrm {[\Omega ]} \ \)は，ワンポイント解説「1.変圧器の巻数比と変圧比，変流比の関係」より，
\[
\begin{eqnarray}
r_{1}^{\prime } &=&\left( \frac {V_{2}}{V_{1}}\right) ^{2}\times r_{1} \\[ 5pt ] &=&\left( \frac {100}{2000}\right) ^{2}\times 0.2 \\[ 5pt ] &=&0.0005 \ \mathrm {[\Omega ]} \\[ 5pt ] x_{1}^{\prime } &=&\left( \frac {V_{2}}{V_{1}}\right) ^{2}\times x_{1} \\[ 5pt ] &=&\left( \frac {100}{2000}\right) ^{2}\times 0.6 \\[ 5pt ] &=&0.0015 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であるから，二次側に換算した変圧器のインピーダンス\( \ {\dot Z}_{2} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
{\dot Z}_{2} &=&r_{1}^{\prime }+\mathrm {j}x_{1}^{\prime }+r_{2}+\mathrm {j}x_{2} \\[ 5pt ] &=&0.0005+\mathrm {j}0.0015+0.0005+\mathrm {j}0.0015 \\[ 5pt ] &=&0.001+\mathrm {j}0.003 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，百分率抵抗降下\( \ p \ \mathrm {[％]} \ \)及び百分率リアクタンス降下\( \ q \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
p &=&\frac {rI_{\mathrm {2n}}}{V_{\mathrm {2n}}} \times 100 \\[ 5pt ] &=&\frac {0.001\times 1000}{100} \times 100 \\[ 5pt ] &=&1 \ \mathrm {[％]} \\[ 5pt ] q &=&\frac {xI_{\mathrm {2n}}}{V_{\mathrm {2n}}} \times 100 \\[ 5pt ] &=&\frac {0.003\times 1000}{100} \times 100 \\[ 5pt ] &=&3 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となるので，百分率インピーダンス降下\( \ ％Z \ \mathrm {[％]} \ \)は，
\[
\begin{eqnarray}
％Z &=&\sqrt {p^{2}+q^{2}} \\[ 5pt ] &=&\sqrt {1^{2}+3^{2}} \\[ 5pt ] &≒&3.16 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(1)
力率\( \ \cos \theta =0.8 \ \)のとき\( \ \sin \theta \ \)は，
\[
\begin{eqnarray}
\sin \theta &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ] &=&\sqrt {1-0.8 ^{2}} \\[ 5pt ] &=&0.6 \\[ 5pt ] \end{eqnarray}
\] であるから，電圧変動率\( \ \varepsilon \ \mathrm {[％]} \ \)は，ワンポイント解説「2.電圧変動率の近似式」の通り，
\[
\begin{eqnarray}
\varepsilon &≃&p\cos \theta +q\sin \theta \\[ 5pt ] &=&1\times 0.8+3\times 0.6 \\[ 5pt ] &=&2.6 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。