Contents
【問題】
【難易度】★★★★☆(やや難しい)
電機子巻線抵抗が\( \ \mathrm {0.2 \ \Omega } \ \)である直流分巻電動機がある。この電動機では界磁抵抗器が界磁巻線に直列に接続されており界磁電流を調整することができる。また,この電動機には定トルク負荷が接続されており,その負荷が要求するトルクは定常状態において回転速度によらない一定値となる。
この電動機を,負荷を接続した状態で端子電圧を\( \ \mathrm {100 \ V } \ \)として運転したところ,回転速度は\( \ \mathrm { \ 1500 \ {min}^{-1}} \ \)であり,電機子電流は\( \ \mathrm {50 \ A } \ \)であった。この状態から,端子電圧を\( \ \mathrm {115 \ V } \ \)に変化させ,界磁電流を端子電圧が\( \ \mathrm {100 \ V } \ \)のときと同じ値に調整したところ,回転速度が変化し最終的にある値で一定となった。この電動機の最終的な回転速度の値\( \ \mathrm {[ {min}^{-1} ] } \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,電機子電流の最終的な値は端子電圧が\( \ \mathrm {100 \ V } \ \)のときと同じである。また,電機子反作用及びブラシによる電圧降下は無視できるものとする。
(1) \( \ 1290 \ \) (2) \( \ 1700 \ \) (3) \( \ 1730 \ \) (4) \( \ 1750 \ \) (5) \( \ 1950 \ \)
【ワンポイント解説】
回転機の計算問題は図1のような等価回路を描けるかどうかが重要です。等価回路はぜひ暗記しておいて下さい。
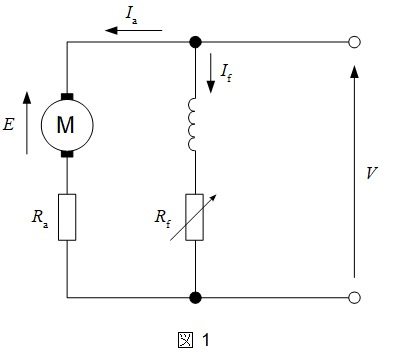
1.直流機の誘導起電力\(E\)とトルク\(T\)
直流機の誘導起電力\( \ E \ \)とトルク\( \ T \ \)は以下の式から導出されます。
\[
\begin{eqnarray}
E&=&\frac {pZ}{60a}\phi N \\[ 5pt ]
&=&k_{\mathrm {e}}\phi N \\[ 5pt ]
T&=&\frac {pZ}{2\pi a}\phi I_{\mathrm {a}} \\[ 5pt ]
&=&k_{\mathrm {t}}\phi I_{\mathrm {a}} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
p&:&磁極数 &Z&&:&電機子導体数 \\[ 5pt ]
a&:&並列回路数 &\phi& &:&磁束 \\[ 5pt ]
N&:&回転速度 &I_{\mathrm {a}}&&:&電機子電流
\end{eqnarray}
\]
【解答】
解答:(4)
電圧変化前後の各部の値を等価回路に記載すると,図2及び図3の通りとなる。
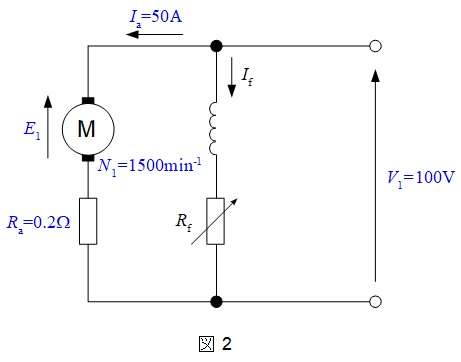
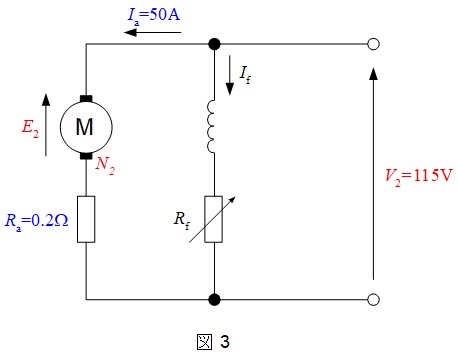
図2において,誘導起電力\( \ E_{1} \ \)は,
\[
\begin{eqnarray}
E_{1}&=&V_{1}-R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ]
&=&100-0.2\times 50 \\[ 5pt ]
&=&90 \ \mathrm {[ V ] }
\end{eqnarray}
\]
と求められる。一方,図3において,電圧変化後の誘導起電力\( \ E_{2} \ \)は,
\[
\begin{eqnarray}
E_{2}&=&V_{2}-R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ]
&=&115-0.2\times 50 \\[ 5pt ]
&=&105 \ \mathrm {[ V ] }
\end{eqnarray}
\]
と求められる。ここで,ワンポイント解説より\( \ E=k_{\mathrm {e}}\phi N \ \)の関係があり,可変抵抗器により\( \ \phi \ \)の値は一定となるので,
\[
\begin{eqnarray}
\frac {E_{2}}{E_{1}}&=&\frac {k_{\mathrm {e}}\phi N_{2}}{k_{\mathrm {e}}\phi N_{1}} \\[ 5pt ]
&=&\frac {N_{2}}{N_{1}} \\[ 5pt ]
\end{eqnarray}
\]
という関係が導かれ,各値を代入すると,
\[
\begin{eqnarray}
&&\frac {E_{2}}{E_{1}}&=&\frac {N_{2}}{N_{1}} \\[ 5pt ]
&⇔&\frac {105}{90}&=&\frac {N_{2}}{1500} \\[ 5pt ]
&⇔&N_{2}&=&1750 \ \mathrm {[ {min}^{-1} ] } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは