Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,三相誘導電動機の誘導起電力に関する記述である。
三相誘導電動機で固定子巻線に電流が流れると\( \ \fbox { (ア) } \ \)が生じ,これが回転子巻線を切るので回転子巻線に起電力が誘導され,この起電力によって回転子巻線に電流が流れることでトルクが生じる。この回転子巻線の電流によって生じる起磁力を\( \ \fbox { (イ) } \ \)ように固定子巻線に電流が流れる。
回転子が停止しているときは,固定子巻線に流れる電流によって生じる\( \ \fbox { (ア) } \ \)は,固定子巻線を切るのと同じ速さで回転子巻線を切る。このことは原理的に変圧器と同じであり,固定子巻線は変圧器の\( \ \fbox { (ウ) } \ \)巻線に相当し,回転子巻線は\( \ \fbox { (エ) } \ \)巻線に相当する。回転子巻線の各相には変圧器と同様に\( \ \fbox { (エ) } \ \)誘導起電力を生じる。
回転子が\( \ n \ \mathrm {[ {min} ^{-1} ]} \ \)の速度で回転しているときは,\( \ \fbox { (ア) } \ \)の速度を\( \ n_{\mathrm {s}} \ \mathrm {[ {min} ^{-1} ]} \ \)とすると,滑り\( \ s \ \)は\( \ \displaystyle s=\frac {n_{\mathrm {s}}-n}{n_{\mathrm {s}}} \ \)で表される。このときの\( \ \fbox { (エ) } \ \)誘導起電力の大きさは,回転子が停止しているときの\( \ \fbox { (オ) } \ \)倍となる。
上記の記述中の空白箇所(ア),(イ),(ウ),(エ)及び(オ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{cccccc}
& (ア) & (イ) & (ウ) & (エ) & (オ) \\
\hline
(1) & 交番磁界 & 打ち消す & 二 次 & 一 次 & 1-s \\
\hline
(2) & 回転磁界 & 打ち消す & 一 次 & 二 次 & \displaystyle \frac {1}{s} \\
\hline
(3) & 回転磁界 & 増加させる & 一 次 & 二 次 & s \\
\hline
(4) & 交番磁界 & 増加させる & 二 次 & 一 次 & \displaystyle \frac {1}{s} \\
\hline
(5) & 回転磁界 & 打ち消す & 一 次 & 二 次 & s \\
\hline
\end{array}
\]
【ワンポイント解説】
三相誘導電動機の原理に関する問題です。
三相誘導電動機は,固定子に\( \ \mathrm {U} \ \)相,\( \ \mathrm {V} \ \)相,\( \ \mathrm {W} \ \)相を\( \ 120° \ \)ずつずらして三相交流を流すことにより回転磁界を発生させます。
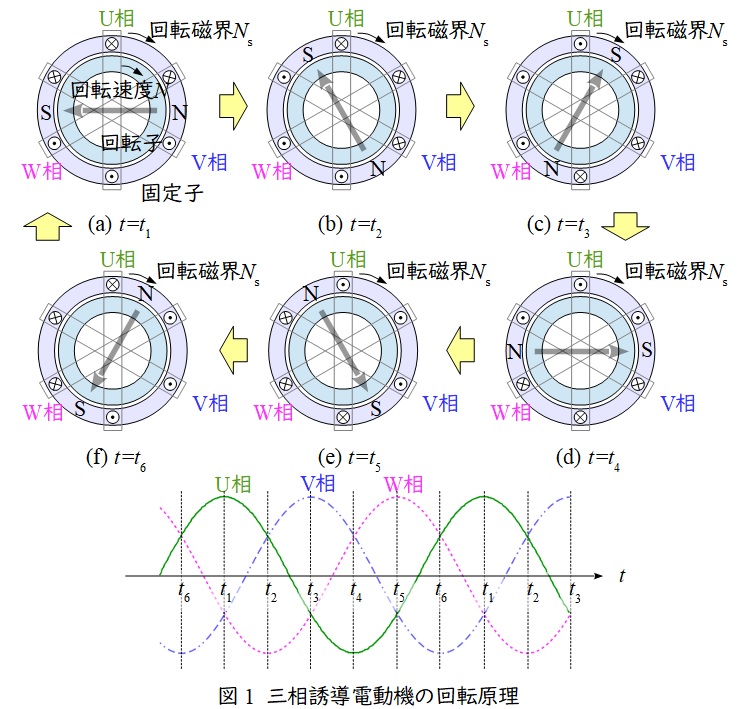
1.三相誘導電動機の回転原理
図1に示すように,\( \ 120° \ \)ずつずらして三つの巻線を配置して,三相交流を流します。
時刻\( \ t_{\mathrm {1}} \ \)においては,\( \ \mathrm {U} \ \)相のみ正,\( \ \mathrm {V} \ \)相と\( \ \mathrm {W} \ \)相が負なので,各巻線の電流の向きは(a)のようになり,これにより発生する磁界は右ねじの法則から図の右側から左側に向かって発生します。
その後\( \ t_{\mathrm {1}} \ → \ t_{\mathrm {2}} \ →\cdots → \ t_{\mathrm {6}} \ \)と徐々に変化していくと,合成磁界も回転していくことがわかります。これにより,回転磁界が生まれ,回転磁界により回転子がそれについていく形で移動することになります。このときの回転磁界の回転速度を同期速度といいます。
2.三相誘導電動機の回転子
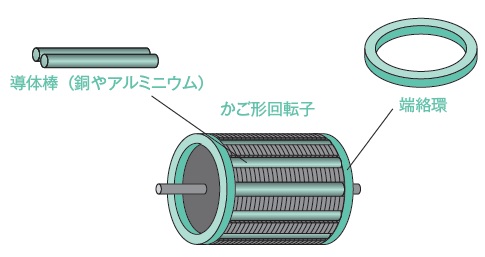
①かご形
かごの形をした導体中に,透磁率の高い鉄心を入れ,両端を端絡環で接続したものです。
構造が簡単で,頑丈かつコンパクトである特徴があります。
出典:みんなが欲しかった!電験三種 機械の実践問題集P.65 TAC出版
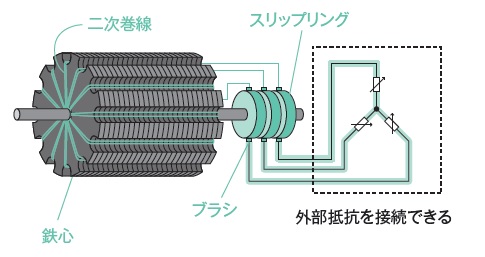
②巻線形
鉄心の外側のスロットに二次巻線を挿入した構造の回転子です。
二次巻線はスリップリングを介して外部の抵抗に接続できるという特徴があります。
出典:みんなが欲しかった!電験三種 機械の実践問題集P.65 TAC出版
3.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \),電源の周波数が\( \ f \ \mathrm {[Hz]} \ \)の時,同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ]
\end{eqnarray}
\]
となります。
4.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \),回転子の回転速度が\( \ N \ \mathrm {[{min}^{-1}]} \ \)である時,誘導機の滑り\( \ s \ \)は,
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
と定義されます。これを整理すると,
\[
\begin{eqnarray}
sN_{\mathrm {s}} &=&N_{\mathrm {s}}-N \\[ 5pt ]
N &=&N_{\mathrm {s}}-sN_{\mathrm {s}} \\[ 5pt ]
&=&N_{\mathrm {s}}\left( 1-s \right) \\[ 5pt ]
\end{eqnarray}
\]
と同期速度から回転速度が導出できます。
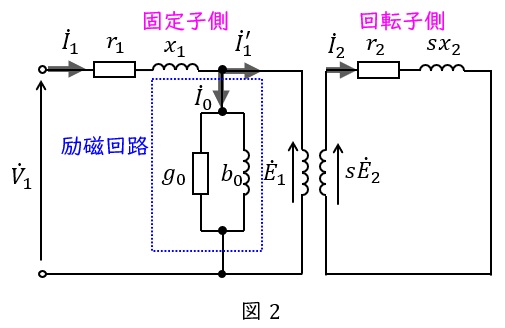
5.三相誘導機の一相分等価回路
三相誘導電動機の一相分等価回路は図2のようになります。ただし,\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流,\( \ {\dot E}_{1} \ \mathrm {[V]} \ \)は一次誘導起電力,\( \ {\dot E}_{2} \ \mathrm {[V]} \ \)は二次誘導起電力,\( \ {\dot I}_{2} \ \mathrm {[A]} \ \)は二次電流,\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流,\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗,\( \ r_{2} \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗,\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス,\( \ x_{2} \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンス,\( \ s \ \)は滑りです。
一次周波数が\( \ f \ \mathrm {[Hz]} \ \)であるとき,滑り\( \ s \ \)で運転中の二次周波数は\( \ sf \ \mathrm {[Hz]} \ \)となるので,二次誘導起電力\( \ {\dot E}_{2} \ \mathrm {[V]} \ \)と二次漏れリアクタンス\( \ x_{2} \ \mathrm {[\Omega ]} \ \)は\( \ s \ \)倍となります。
等価回路はL形簡易等価回路を覚えておけば良いでしょう。
【解答】
解答:(5)
(ア)
ワンポイント解説「1.三相誘導電動機の回転原理」の通り,固定子巻線に三相交流が流れると回転磁界が発生します。
(イ)
固定子巻線には回転子巻線の電流によって生じる起磁力を打ち消すように電流が流れます。理論科目の電磁気で学習するファラデーの電磁誘導の法則によるものです。
(ウ)
ワンポイント解説「5.三相誘導機の一相分等価回路」の通り,固定子巻線は変圧器の一次巻線に相当します。
(エ)
ワンポイント解説「5.三相誘導機の一相分等価回路」の通り,回転子巻線は変圧器の二次巻線に相当します。
(オ)
ワンポイント解説「5.三相誘導機の一相分等価回路」の通り,二次誘導起電力の大きさは停止時の\( \ s \ \)倍になります。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは