《機械》〈回転機〉[R4上:問7]電源電圧及びトルク一定時の各種電動機の特性に関する論説問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

電源電圧一定の下，トルク一定の負荷を負って回転している各種電動機の性質に関する記述として，正しいものと誤りのものの組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。

(ア)　巻線形誘導電動機の二次抵抗を大きくすると，滑りは増加する。

(イ)　力率\( \ 1.0 \ \)で運転している同期電動機の界磁電流を小さくすると，電機子電流の位相は電源電圧に対し，進みとなる。

(ウ)　他励直流電動機の界磁電流を大きくすると，回転速度は上昇する。

(エ)　かご形誘導電動機の電源周波数を高くすると励磁電流は増加する。

\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 　誤り　 & 　誤り　 & 　正しい　 & 　正しい　 \\
\hline
(2) & 　正しい　 & 　正しい　 & 　誤り　 & 　誤り　 \\
\hline
(3) & 　誤り　 & 　正しい　 & 　正しい　 & 　正しい　 \\
\hline
(4) & 　正しい　 & 　誤り　 & 　誤り　 & 　正しい　 \\
\hline
(5) & 　正しい　 & 　誤り　 & 　誤り　 & 　誤り　 \\
\hline
\end{array}
\]

【ワンポイント解説】

各種電動機の特性に関する問題です。
問題が多岐にわたる内容であるため，幅広い知識が必要となります。特に（ウ）と（エ）が瞬時に分かる受験生は少なかったと予想されます。

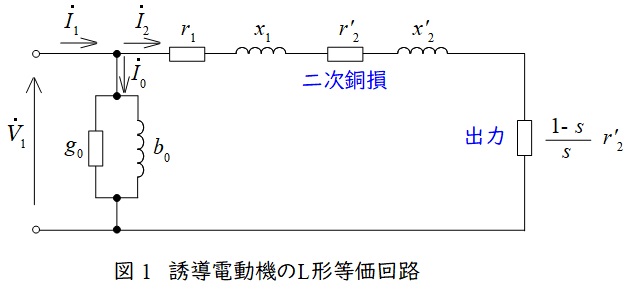
1.誘導電動機の\( \ \mathrm {L} \ \)形等価回路
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において，\( \ {\dot V}_{1} \ \)は一次側端子電圧，\( \ {\dot I}_{1} \ \)は一次電流，\( \ {\dot I}_{2} \ \)は二次電流，\( \ {\dot I}_{0} \ \)は励磁電流，\( \ r_{1} \ \)は一次巻線抵抗，\( \ r_{2}^{\prime } \ \)は二次巻線抵抗の一次換算，\( \ x_{1} \ \)は一次漏れリアクタンス，\( \ x_{2}^{\prime } \ \)は二次漏れリアクタンスの一次換算，\( \ s \ \)は滑りとなります。

2.巻線形誘導電動機のトルクの比例推移
三相誘導電動機のトルク\( \ T \ \)は，
\[
\begin{eqnarray}
T &=& \frac {1}{\omega _{\mathrm {s}}}\frac {3V_{1}^{2}\displaystyle \frac {r_{2}^{\prime }}{s}}{\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ] \end{eqnarray}
\] であり，\( \ 1≫s \ \)の時，\( \ r_{2}^{\prime } \ \)以外の抵抗やリアクタンスは無視できるので，
\[
\begin{eqnarray}
T &≃& \frac {3V_{1}^{2}s}{\omega _{\mathrm {s}}r_{2}^{\prime }} \\[ 5pt ] \end{eqnarray}
\] となり，トルクに対する変数は可変抵抗である二次抵抗\( \ r_{2}^{\prime } \ \)と滑り\( \ s \ \)のみであり，トルク\( \ T \ \)を一定とすると，
\[
\begin{eqnarray}
\frac {r_{2}^{\prime }}{s} &=& 一定 \\[ 5pt ] \end{eqnarray}
\] の関係があります。

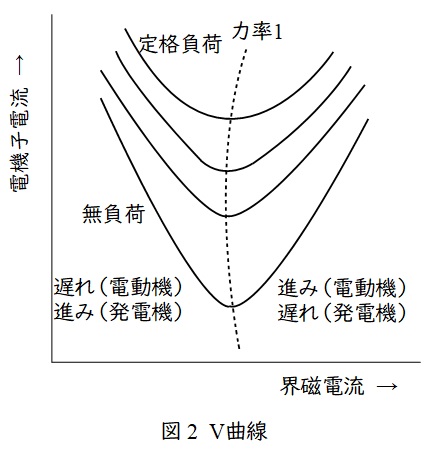
3.同期機の\( \ \mathrm {V} \ \)曲線
同期機の界磁電流と電機子電流の関係である\( \ \mathrm {V} \ \)曲線（位相特性曲線）は図2のようになります。
力率\( \ 1 \ \)を最小値として界磁電流を大きくすれば，電動機の場合進み位相となり，界磁電流を小さくすれば遅れ位相となります。また，発電機の場合は逆となります。
また，負荷が大きくなると曲線は上側に移動し，同じ力率においては電機子電流が大きくなります。

4.直流他励電動機の等価回路
図3に直流他励電動機の等価回路を示します。図3において，\( \ V \ \)は端子電圧，\( \ E \ \)は逆起電力，\( \ V_{\mathrm {f}} \ \)は界磁電圧，\( \ I_{\mathrm {a}} \ \)は電機子電流，\( \ I_{\mathrm {f}} \ \)は界磁電流，\( \ R_{\mathrm {a}} \ \)は電機子抵抗，\( \ R_{\mathrm {f}} \ \)は界磁抵抗となります。
他励式の特徴としては，界磁回路が独立しているので，界磁磁束を独立して制御できるという特徴があります。

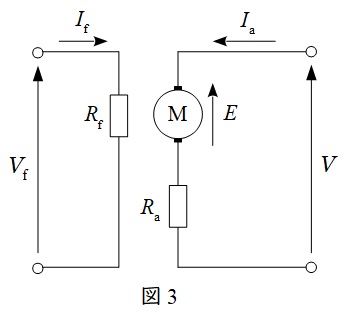
また，上記の等価回路にキルヒホッフの法則を適用すると，以下の関係式が導き出せることが分かります。
\[
\begin{eqnarray}
V &=& E+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] I_{\mathrm {f}} &=& \frac {V_{\mathrm {f}}}{R_{\mathrm {f}}} \\[ 5pt ] \end{eqnarray}
\]

5.直流電動機の速度制御法
磁極の数\( \ p \ \)，電機子導体数\( \ Z \ \)，電機子巻線並列回路数\( \ a \ \)，各極の磁束\( \ \phi \ \)，回転速度\( \ N \ \)とすると，直流機の誘導起電力(逆起電力)\( \ E \ \)は，
\[
\begin{eqnarray}
E &=&\frac {pZ}{60a}\phi N \\[ 5pt ] &=&k_{\mathrm {e}}\phi N \\[ 5pt ] \end{eqnarray}
\] となり，磁束\( \ \phi \ \)と回転速度\( \ N \ \)に比例します。また，図3の他励直流電動機の等価回路より，
\[
\begin{eqnarray}
E &=&k_{\mathrm {e}}\phi N =V-R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] の関係があるため，\( \ N \ \)について整理すると，
\[
\begin{eqnarray}
N &=&\frac {V-R_{\mathrm {a}}I_{\mathrm {a}}}{k_{\mathrm {e}}\phi } \\[ 5pt ] \end{eqnarray}
\] となり，界磁\( \ \phi \ \)，電機子抵抗\( \ R_{\mathrm {a}} \ \)，電源電圧\( \ V \ \)で回転速度\( \ N \ \)を制御することができ，それぞれ界磁制御法，抵抗制御法，電圧制御法と呼ばれます。