《機械》〈パワーエレクトロニクス〉[H30:問16]降圧チョッパに関する計算問題

【問題】

【難易度】★★★☆☆（普通）

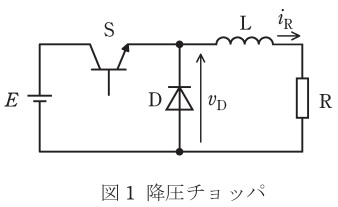
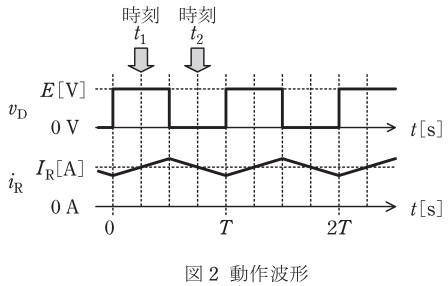
図1に示す降圧チョッパの回路は，電圧\( \ E \ \)の直流電源，スイッチングする半導体バルブデバイス\( \ \mathrm {S} \ \)，ダイオード\( \ \mathrm {D} \ \)，リアクトル\( \ \mathrm {L} \ \)，及び抵抗\( \ \mathrm {R} \ \)の負荷から構成されている。また，図2には，図1の回路に示すダイオード\( \ \mathrm {D} \ \)の電圧\( \ v_{\mathrm {D}} \ \)と負荷の電流\( \ i_{\mathrm {R}} \ \)の波形を示す。次の(a)及び(b)の問に答えよ。

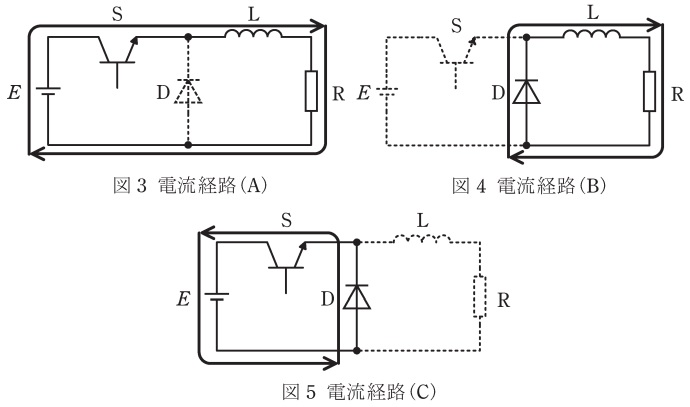
(a)　降圧チョッパの回路動作に関し，図3～図5に，実線で示した回路に流れる電流のループと方向を示した三つの電流経路を考える。図2の時刻\( \ t_{1} \ \)及び時刻\( \ t_{2} \ \)において，それぞれどの電流経路となるか。正しい組合せを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{ccc}
& 時刻 \ t_{1} & 時刻 \ t_{2} \\
\hline
(1) & 　電流経路\left( \mathrm {A} \right)　 & 　電流経路\left( \mathrm {B} \right)　 \\
\hline
(2) & 　電流経路\left( \mathrm {A} \right)　 & 　電流経路\left( \mathrm {C} \right)　 \\
\hline
(3) & 　電流経路\left( \mathrm {B} \right)　 & 　電流経路\left( \mathrm {A} \right)　 \\
\hline
(4) & 　電流経路\left( \mathrm {B} \right)　 & 　電流経路\left( \mathrm {C} \right)　 \\
\hline
(5) & 　電流経路\left( \mathrm {C} \right)　 & 　電流経路\left( \mathrm {B} \right)　 \\
\hline
\end{array}
\]

(b)　電圧\( \ E \ \)が\( \ 100 \ \mathrm {V} \ \)，降圧チョッパの通流率が\( \ 50 \ ％ \ \)，負荷抵抗\( \ R \ \)が\( \ 2 \ \Omega \ \)とする。デバイス\( \ \mathrm {S} \ \)は周期\( \ T \ \)の高周波でスイッチングし，リアクトル\( \ \mathrm {L} \ \)の平滑作用により，図2に示す電流\( \ i_{\mathrm {R}} \ \)のリプル成分は十分小さいとする。電流\( \ i_{\mathrm {R}} \ \)の平均値\( \ I_{\mathrm {R}} \ \mathrm {[A]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 17.7 \ \)　　(2)　\( \ 25.0 \ \)　　(3)　\( \ 35.4 \ \)　　(4)　\( \ 50.1 \ \)　　(5)　\( \ 70.7 \ \)

【ワンポイント解説】

パワーエレクトロニクスの問題は公式の丸暗記では応用が利かないので，回路のメカニズムを理解することが重要となります。本問(a)ではメカニズムを理解することができ，(b)ではその結果どうなるかを理解できるので，学習教材としては非常に良い問題と言えます。

1.降圧チョッパ
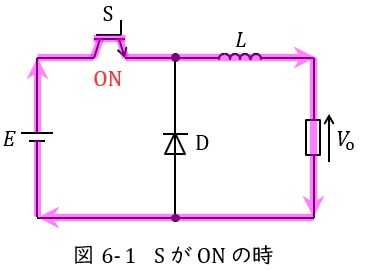
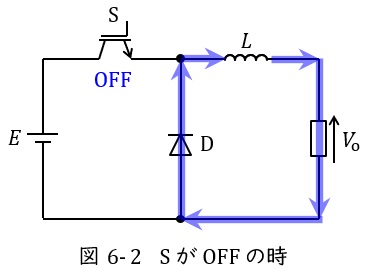
図6-1及び図6-2は降圧チョッパの例を示します。
スイッチ\( \ \mathrm {S} \ \)がオンになると，図6-1のように電源からの電流はスイッチ\( \ \mathrm {S} \ \)を通り，リアクトル\( \ L \ \)側に電流が流れますが，ダイオード\( \ \mathrm {D} \ \)は逆向きなので電流が流れません。
スイッチ\( \ \mathrm {S} \ \)がオフになると，図6-2のように電源から電流は流れず，リアクトル\( \ L \ \)に蓄えられているエネルギーから出力側と還流ダイオード\( \ \mathrm {D} \ \)に電流が流れます。
したがって降圧チョッパの出力電圧の平均値\( \ V_{\mathrm {o}} \ \)は，スイッチのオン時間を\( \ T_{\mathrm {on}} \ \)，オフ時間を\( \ T_{\mathrm {off}} \ \)とすると，
\[
\begin{eqnarray}
V_{\mathrm {o}}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}E \\[ 5pt ] \end{eqnarray}
\] で求められます。このとき，\( \ E \ \)の係数
\[
\begin{eqnarray}
\gamma &=&\frac {T_{\mathrm {ON}}}{T_{\mathrm {ON}}+T_{\mathrm {OFF}}} \\[ 5pt ] \end{eqnarray}
\] を通流率といいます。

【関連する「電気の神髄」記事】

　　降圧チョッパ回路の理論

【解答】

(a)解答：(1)
ワンポイント解説「1.降圧チョッパ」の通り，スイッチ\( \ \mathrm {S} \ \)が\( \ \mathrm {ON} \ \)の時，電流は電源\( \ E \ \)から流れ図3に示すような電流経路\( \ \mathrm {(A)} \ \)となり，スイッチ\( \ \mathrm {S} \ \)が\( \ \mathrm {OFF} \ \)の時，リアクトル\( \ \mathrm {L} \ \)に蓄えられたエネルギーが放出され，図4に示すような電流経路\( \ \mathrm {(B)} \ \)となります。時刻\( \ t_{1} \ \)では\( \ v_{\mathrm {D}}=E \ \mathrm {[V]} \ \)なのでスイッチ\( \ \mathrm {S} \ \)は\( \ \mathrm {ON} \ \)，時刻\( \ t_{2} \ \)では\( \ v_{\mathrm {D}}=0 \ \mathrm {[V]} \ \)なのでスイッチ\( \ \mathrm {S} \ \)は\( \ \mathrm {OFF} \ \)となります。

よって，時刻\( \ t_{1} \ \)では電流経路\( \ \mathrm {(A)} \ \)，時刻\( \ t_{2} \ \)では電流経路\( \ \mathrm {(B)} \ \)と求められます。

(b)解答：(2)
電源電圧\( \ E=100 \ \mathrm {[V]} \ \)，通流率\( \ \gamma =0.5 \ \)であるから，降圧チョッパの平均出力電圧\( \ V_{\mathrm {o}} \ \mathrm {[V]} \ \)は，ワンポイント解説「1.降圧チョッパ」の通り，
\[
\begin{eqnarray}
V_{\mathrm {o}} &=&\frac {T_{\mathrm {ON}}}{T_{\mathrm {ON}}+T_{\mathrm {OFF}}}E \\[ 5pt ] &=&\gamma E \\[ 5pt ] &=&0.5\times 100 \\[ 5pt ] &=&50 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，負荷抵抗\( \ R=2 \ \mathrm {[\Omega ]} \ \)であるので，電流\( \ i_{\mathrm {R}} \ \)の平均値\( \ I_{\mathrm {R}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {R}} &=&\frac {V_{\mathrm {o}}}{R} \\[ 5pt ] &=&\frac {50}{2} \\[ 5pt ] &=&25 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。