《機械》〈回転機〉[R3:問2]直流分巻電動機の端子電圧を調整したときのトルク変化に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

ある直流分巻電動機を端子電圧\( \ 220 \ \mathrm {V} \ \)，電機子電流\( \ 100 \ \mathrm {A} \ \)で運転したときの出力が\( \ 18.5 \ \mathrm {kW} \ \)であった。

この電動機の端子電圧と界磁抵抗とを調節して，端子電圧\( \ 200 \ \mathrm {V} \ \)，電機子電流\( \ 110 \ \mathrm {A} \ \)，回転速度\( \ 720 \ \mathrm {min^{-1}} \ \)で運転する。このときの電動機の発生トルクの値\( \ \mathrm {[N\cdot m]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，ブラシの接触による電圧降下及び電機子反作用は無視でき，電機子抵抗の値は上記の二つの運転において等しく，一定であるものとする。

　(1)　\( \ 212 \ \)　　(2)　\( \ 236 \ \)　　(3)　\( \ 245 \ \)　　(4)　\( \ 260 \ \)　　(5)　\( \ 270 \ \)

【ワンポイント解説】

直流分巻電動機の計算問題です。
直流機の計算問題は等価回路が与えられることはほとんどなく，自分で等価回路を描き，関係式を導出することが重要となります。
毎年のように出題される分野なので，演習を繰り返し計算パターンを覚えるようにしましょう。

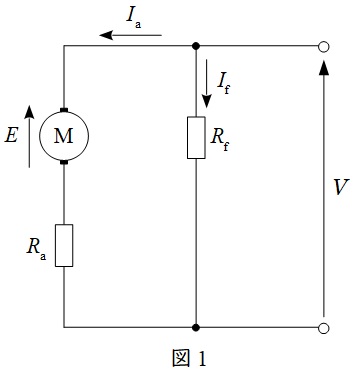
1.分巻電動機の等価回路と特性
分巻電動機の等価回路を図1に示します。ただし，図において，\( \ E \ \mathrm {[V]} \ \)は逆起電力，\( \ V \ \mathrm {[V]} \ \)は端子電圧，\( \ I_{\mathrm {a}} \ \mathrm {[A]} \ \)は電機子電流，\( \ I_{\mathrm {f}} \ \mathrm {[A]} \ \)は界磁電流，\( \ R_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)は電機子抵抗，\( \ R_{\mathrm {f}} \ \mathrm {[\Omega ]} \ \)は界磁抵抗です。
磁束を\( \ \phi \ \mathrm {[Wb]} \ \)，回転速度を\( \ N \ \mathrm {[min^{-1}]} \ \)とすると，\( \ \phi ∝ I_{\mathrm {f}} \ \)となるので，逆起電力\( \ E \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
E &=&k_{\mathrm {e}}\phi N \\[ 5pt ] &=&k_{\mathrm {e}}^{\prime } I_{\mathrm {f}} N \\[ 5pt ] \end{eqnarray}
\] となります。またトルク\( \ T \ \mathrm {[N\cdot m]} \ \)は，
\[
\begin{eqnarray}
T &=&k_{\mathrm {f}}\phi I_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] となります。このときの電動機の出力\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P &=&EI_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

2.直流電動機の出力\( \ P \ \mathrm {[W]} \ \)とトルク\( \ T \ \mathrm {[N\cdot m]} \ \)の関係
直流電動機の出力\( \ P \ \mathrm {[W]} \ \)とトルク\( \ T \ \mathrm {[N\cdot m]} \ \)の関係は，角速度\( \ \omega \ \mathrm {[rad / s]} \ \)とすると，
\[
\begin{eqnarray}
P &=&\omega T \\[ 5pt ] \end{eqnarray}
\] の関係があり，このときの回転速度が\( \ N \ \mathrm {[min^{-1}]} \ \)であるとき，\( \ \displaystyle \omega =\frac {2\pi N}{60} \ \)の関係より，
\[
\begin{eqnarray}
P &=&\frac {2\pi N}{60} T \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(2)
端子電圧\( \ V=220 \ \mathrm {[V]} \ \)，電機子電流\( \ I_{\mathrm {a}}=100 \ \mathrm {[A]} \ \)で運転したときの出力\( \ P=18.5 \ \mathrm {[kW]} \ \)であるから，ワンポイント解説「1.分巻電動機の等価回路と特性」より，逆起電力\( \ E \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
E &=&\frac {P}{I_{\mathrm {a}}} \\[ 5pt ] &=&\frac {18.5\times 10^{3}}{100} \\[ 5pt ] &=&185 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。このとき，図1より\( \ V=E+R_{\mathrm {a}}I_{\mathrm {a}} \ \)の関係があるから，
\[
\begin{eqnarray}
V &=&E+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] 220&=&185+R_{\mathrm {a}}\times 100 \\[ 5pt ] R_{\mathrm {a}}&=&\frac {220-185}{100} \\[ 5pt ] &=&0.35 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。
端子電圧と界磁抵抗とを調節して，端子電圧\( \ V^{\prime }=200 \ \mathrm {[V]} \ \)，電機子電流\( \ I_{\mathrm {a}}^{\prime }=110 \ \mathrm {A} \ \)，回転速度\( \ N^{\prime }=720 \ \mathrm {min^{-1}} \ \)としたときの逆起電力\( \ E^{\prime } \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
E^{\prime } &=&V^{\prime }-R_{\mathrm {a}}I_{\mathrm {a}}^{\prime } \\[ 5pt ] &=&200-0.35\times 110 \\[ 5pt ] &=&161.5 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となるので，出力\( \ P^{\prime } \ \mathrm {[W]} \ \)
\[
\begin{eqnarray}
P^{\prime } &=&E^{\prime }I_{\mathrm {a}}^{\prime } \\[ 5pt ] &=&161.5\times 110 \\[ 5pt ] &=&17765 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「2.直流電動機の出力\( \ P \ \mathrm {[W]} \ \)とトルク\( \ T \ \mathrm {[N\cdot m]} \ \)の関係」の通り，このときのトルク\( \ T^{\prime } \ \mathrm {[N\cdot m]} \ \)は，
\[
\begin{eqnarray}
T^{\prime } &=&\frac {P^{\prime }}{\omega } \\[ 5pt ] &=&\frac {P^{\prime }}{\displaystyle \frac {2\pi N^{\prime }}{60}} \\[ 5pt ] &=&\frac {60P^{\prime }}{2\pi N^{\prime }} \\[ 5pt ] &=&\frac {60\times 17765}{2\pi \times 720} \\[ 5pt ] &≒&236 \ \mathrm {[N\cdot m]} \\[ 5pt ] \end{eqnarray}
\] と求められる。