《機械》〈変圧器〉[R4上:問8]短絡試験結果からの漏れリアクタンスの導出に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

単相変圧器の一次側に電流計，電圧計及び電力計を接続して，短絡試験を行う。二次側を短絡し，一次側に定格周波数の電圧を供給し，電流計が$\ 40 \ \mathrm {A} \ $を示すように一次側の電圧を調整したところ，電圧計は$\ 80 \ \mathrm {V} \ $，電力計は$\ 1 \ 000 \ \mathrm {W} \ $を示した。この変圧器の一次側からみた漏れリアクタンスの値$\ \mathrm {[\Omega ]} \ $として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，変圧器の励磁回路のインピーダンスは無視し，電流計，電圧計及び電力計は理想的な計器であるものとする。

　(1)　$\ 0.63 \ $　　(2)　$\ 1.38 \ $　　(3)　$\ 1.90 \ $　　(4)　$\ 2.00 \ $　　(5)　$\ 2.10 \ $

【ワンポイント解説】

単相変圧器の短絡試験からの漏れリアクタンスの導出に関する問題です。
出題パターンとしては決まったパターンばかりなので，本問の導出方法を覚えてしまうようにしましょう。
短絡試験に合わせて無負荷試験の内容も理解しておくと良いかと思います。

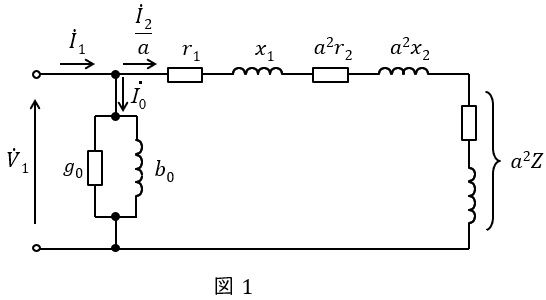
1.変圧器の等価回路（一次換算）
変圧器の一次換算等価回路を図1に示します。ただし，$\ {\dot V}_{1} \ \mathrm {[V]} \ $は一次側端子電圧，$\ {\dot I}_{1} \ \mathrm {[A]} \ $は一次電流，$\ {\dot I}_{2} \ \mathrm {[A]} \ $は二次電流，$\ {\dot I}_{0} \ \mathrm {[A]} \ $は励磁電流，$\ r_{1} \ \mathrm {[\Omega ]} \ $は一次巻線抵抗，$\ r_{2} \ \mathrm {[\Omega ]} \ $は二次巻線抵抗，$\ x_{1} \ \mathrm {[\Omega ]} \ $は一次漏れリアクタンス，$\ x_{2} \ \mathrm {[\Omega ]} \ $は二次漏れリアクタンス，$\ a \ $は変圧比（巻数比）となります。

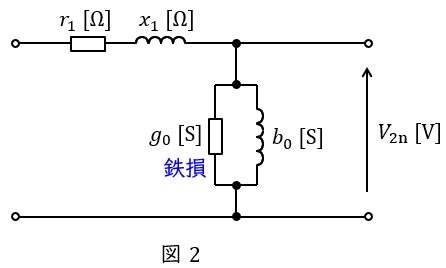
2.無負荷試験の等価回路
変圧器の無負荷試験は一次側を開放して，二次側に定格電圧を加える試験です。測定される電力は鉄損となり，測定される電力と電流から，励磁コンダクタンス$\ g_{0} \ \mathrm {[S]} \ $及び励磁サセプタンス$\ b_{0} \ \mathrm {[S]} \ $を求めることが可能となります。二次側に定格電圧を加えるのが一般的ですが，二次側開放で一次側に定格電圧を加えても同様に求められます。

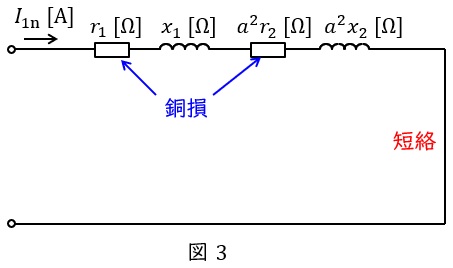
3.短絡試験の等価回路
変圧器の短絡試験は二次側を短絡して，一次側にインピーダンス電圧を加えて，定格電流を流す試験です。励磁回路に流れる電流が十分に小さいと仮定すると，測定される電力は銅損となります。測定される電力と電流から，高圧側換算の巻線抵抗$\ R=r_{1}+a^{2}r_{2} \ \mathrm {[\Omega ]} \ $を求めることが可能となります

【解答】

解答：(3)
図3の短絡試験の等価回路において，短絡試験時の電圧$\ V_{\mathrm {s}}=80 \ \mathrm {[V]} \ $，電流$\ I_{\mathrm {s}}=40 \ \mathrm {[A]} \ $であるから，変圧器の一次側から見た合成インピーダンス$\ Z \ \mathrm {[\Omega ]} \ $は，
$$\begin{eqnarray} Z &=& \frac {V_{\mathrm {s}}}{I_{\mathrm {s}}} \\[ 5pt ] &=& \frac {80}{40} \\[ 5pt ] &=& 2 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}$$ であり，短絡試験時の電力$\ P_{\mathrm {s}}=1 \ 000 \ \mathrm {[W]} \ $より，一次側から見た抵抗$\ R\left( =r_{1}+a^{2}r_{2}\right) \ \mathrm {[\Omega ]} \ $は，
$$\begin{eqnarray} P_{\mathrm {s}} &=& RI_{\mathrm {s}}^{2} \\[ 5pt ] R&=& \frac {P_{\mathrm {s}}}{I_{\mathrm {s}}^{2}} \\[ 5pt ] &=& \frac {1 \ 000}{40^{2}} \\[ 5pt ] &=& 0.625 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}$$ となる。したがって，$\ Z=\sqrt {R^{2}+X^{2}} \ $の関係から一次側から見た漏れリアクタンス$\ X \ \mathrm {[\Omega ]} \ $は，
$$\begin{eqnarray} Z^{2}&=&R^{2}+X^{2} \\[ 5pt ] X &=& \sqrt {Z^{2}-R^{2}} \\[ 5pt ] &=& \sqrt {2^{2}-0.625^{2}} \\[ 5pt ] &≒& 1.90 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}$$ と求められる。