【問題】
【難易度】★★★★☆(やや難しい)
変圧器に関する記述として,誤っているものを次の(1)~(5)のうちから一つ選べ。
(1) 無負荷の変圧器の一次巻線に正弦波交流電圧を加えると,鉄心には磁気飽和現象やヒステリシス現象が生じるので電流は非正弦波電流となる。この電流を励磁電流といい,第\( \ 3 \ \)次をはじめとする多くの次数の高調波を含む。
(2) 変圧器の励磁電流のうち,一次電圧と同相成分を鉄損電流,\( \ \displaystyle \frac {\pi }{2} \ \mathrm {[rad]} \ \)遅れた成分を磁化電流という。
(3) 変圧器の鉄損には主にヒステリシス損と渦電流損がある。電源の周波数を\( \ f \ \),鉄心に用いる電磁鋼板の厚さを\( \ t \ \)とすると,ヒステリシス損は\( \ f \ \)に比例し,渦電流損は\( \ \left( f\times t\right) \ \)の\( \ 2 \ \)乗に比例する。ただし,鉄心の磁束密度を同一とする。
(4) 変圧器の損失には主に鉄損と銅損があり,両者が等しくなったときに最大効率となる。無負荷損の主なものは鉄損で,電圧と周波数が一定であれば負荷に関係なく一定である。また,負荷損の主なものは銅損で,負荷電流の\( \ 2 \ \)乗に比例する。
(5) 変圧器の等価回路において,励磁回路は励磁コンダクタンスと励磁サセプタンスで構成される。両者を合わせて励磁アドミタンスという。励磁コンダクタンスに流れる電流は磁化電流に対応し,励磁サセプタンスで発生する損失は鉄損に対応している。
【ワンポイント解説】
変圧器の損失と特性に関する問題です。問題文が非常に長く,解くのに時間を要する問題です。
よく読んでいくと(2)の内容と(5)の内容が矛盾しているのが読み取れるので,その辺りにピンと来た受験生が比較的早く解けたのではないかなと思います。
1.変圧器の等価回路(一次換算)と鉄損及び銅損
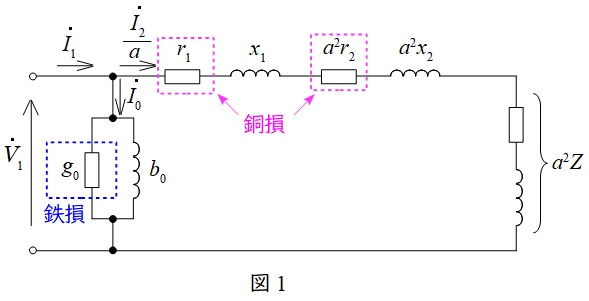
変圧器の一次側換算等価回路を図1に示します。ただし,\( \ {\dot V}_{1} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \)は一次電流,\( \ {\dot I}_{2} \ \)は二次電流,\( \ {\dot I}_{0} \ \)は励磁電流,\( \ r_{1} \ \)は一次巻線抵抗,\( \ r_{2} \ \)は二次巻線抵抗,\( \ x_{1} \ \)は一次漏れリアクタンス,\( \ x_{2} \ \)は二次漏れリアクタンス,\( \ g_{0} \ \)は励磁コンダクタンス,\( \ b_{0} \ \)は励磁サセプタンス,\( \ a \ \)は変圧比(巻数比)となります。
等価回路より,鉄損は電圧\( \ {\dot V}_{1} \ \)の\( \ 2 \ \)乗に比例し,銅損は電流\( \ {\dot I}_{2} \ \)の\( \ 2 \ \)乗に比例することがわかります。
2.変圧器の損失
1.無負荷損(鉄損)
1-1.ヒステリシス損\( \ W_{\mathrm {h}} \ \)
交番磁界によって磁性体の磁区の向きが変化します。これに伴って発生する損失をヒステリシス損と言い,以下の式で求められます。
\[
\begin{eqnarray}
W_{\mathrm {h}} &≒& K_{\mathrm {h}}fB_{\mathrm {m}}^{2} \\[ 5pt ]
&=& K_{\mathrm {h}}^{\prime }\frac {V^{2}}{f} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&&K_{\mathrm {h}},K_{\mathrm {h}}^{\prime }:比例定数, f:周波数 \\[ 5pt ]
&&B_{\mathrm {m}}:最大磁束密度,V:電源電圧 \\[ 5pt ]
\end{eqnarray}
\]
したがって,\( \ B_{\mathrm {m}} \ \)一定の時\( \ W_{\mathrm {h}} \ \)は\( \ f \ \)に比例し,\( \ V \ \)一定の時\( \ W_{\mathrm {h}} \ \)は\( \ f \ \)に反比例します。
1-2.渦電流損\( \ W_{\mathrm {e}} \ \)
鉄心内で交番磁界の磁束変化が起きると鉄心内に起電力が生じ渦電流が生じます。これに伴って発生する損失を渦電流損と言い,以下の式で求められます。
\[
\begin{eqnarray}
W_{\mathrm {e}} &≒& K_{\mathrm {e}}\left( tfB_{\mathrm {m}}\right) ^{2} \\[ 5pt ]
&=& K_{\mathrm {e}}^{\prime }V^{2} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&&K_{\mathrm {e}},K_{\mathrm {e}}^{\prime }:比例定数, f:周波数 \\[ 5pt ]
&&B_{\mathrm {m}}:最大磁束密度,V:電源電圧,t:鉄板の厚さ \\[ 5pt ]
\end{eqnarray}
\]
したがって,\( \ B_{\mathrm {m}} \ \)一定の時\( \ W_{\mathrm {h}} \ \)は\( \ f \ \)の\( \ 2 \ \)乗に比例し,\( \ V \ \)一定の時\( \ W_{\mathrm {h}} \ \)は\( \ f \ \)に関係なく一定となります。
2.負荷損
2-1.銅損\( \ W_{\mathrm {c}} \ \)
変圧器の一次巻線及び二次巻線にて生じる抵抗損で,負荷の\( \ 2 \ \)乗に比例して増加します。
2-2.漂遊負荷損\( \ W_{\mathrm {s}} \ \)
変圧器での漏れ磁束による損失で,銅損よりかなり小さい値のため,試験ではほぼ無視する場合が多いです。
3.変圧器の効率\( \ \eta \ \)と最大効率\( \ \eta _{\mathrm {m}} \ \)
変圧器の損失は鉄損\( \ p_{\mathrm {i}} \ \)と銅損\( \ p_{\mathrm {c}} \ \)があり,\( \ p_{\mathrm {i}} \ \)は負荷によらず一定であり,\( \ p_{\mathrm {c}} \ \)は負荷(電流)の\( \ 2 \ \)乗に比例します。従って,定格出力\( \ P_{\mathrm {n}} \ \)で利用率\( \ \alpha \ \)の時の変圧器の効率\( \ \eta \ \)は,
\[
\begin{eqnarray}
\eta &=&\frac {出力}{入力} \\[ 5pt ]
&=&\frac {出力}{出力+損失} \\[ 5pt ]
&=&\frac {\alpha P_{\mathrm {n}}}{\alpha P_{\mathrm {n}}+p_{\mathrm {i}}+\alpha ^{2}p_{\mathrm {c}}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
次に,最大効率\( \ \eta _{\mathrm {m}} \ \)を求めます。上式の分母分子を\( \ \alpha \ \)で割ると
\[
\begin{eqnarray}
\eta &=&\frac {P_{\mathrm {n}}}{\displaystyle P_{\mathrm {n}}+\frac {p_{\mathrm {i}}}{\alpha }+\alpha p_{\mathrm {c}}} \\[ 5pt ]
\end{eqnarray}
\]
となり,効率が最大となるためには,上式の分母が最小となれば良いです。よって,\( \ \displaystyle A=P_{\mathrm {n}}+\frac {p_{\mathrm {i}}}{\alpha }+\alpha p_{\mathrm {c}} \ \)と置くと,
\[
\begin{eqnarray}
\frac {\mathrm {d}A}{\mathrm {d}\alpha }&=&-\frac {p_{\mathrm {i}}}{\alpha ^{2} }+p_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
となります。よって\( \ \displaystyle \frac {\mathrm {d}A}{\mathrm {d}\alpha }=0 \ \)となるとき,\( \ p_{\mathrm {i}}=\alpha ^{2}p_{\mathrm {c}} \ \)であり,鉄損と銅損が等しい時効率は最大となります。
※ 電験\( \ 3 \ \)種においては,鉄損と銅損が等しい時,効率が最大となることを覚えていれば問題ありません。
【関連する「電気の神髄」記事】
【解答】
解答:(5)
(1)正しい
問題文の通り,無負荷の変圧器の一次巻線に正弦波交流電圧を加えると,鉄心には磁気飽和現象やヒステリシス現象が生じるので電流は非正弦波電流となります。この電流を励磁電流といい,第\( \ 3 \ \)次をはじめとする多くの次数の高調波を含みます。
(2)正しい
ワンポイント解説「1.変圧器の等価回路(一次換算)と鉄損及び銅損」図1に示す変圧器の励磁電流のうち,励磁コンダクタンス\( \ g_{0} \ \)に流れる一次電圧と同相成分を鉄損電流,励磁サセプタンス\( \ b_{0} \ \)に流れる\( \ \displaystyle \frac {\pi }{2} \ \mathrm {[rad]} \ \)遅れた成分遅れた成分を磁化電流といいます。
(3)正しい
ワンポイント解説「2.変圧器の損失」の通り,電源の周波数を\( \ f \ \),鉄心に用いる電磁鋼板の厚さを\( \ t \ \)とすると,ヒステリシス損は\( \ f \ \)に比例し,渦電流損は\( \ \left( f\times t\right) \ \)の\( \ 2 \ \)乗に比例します。
(4)正しい
ワンポイント解説「3.変圧器の効率\( \ \eta \ \)と最大効率\( \ \eta _{\mathrm {m}} \ \)」の通り,変圧器の損失には主に鉄損と銅損があり,両者が等しくなったときに最大効率となります。無負荷損の主なものは鉄損で,電圧と周波数が一定であれば負荷に関係なく一定であり,負荷損の主なものは銅損で,負荷電流の\( \ 2 \ \)乗に比例します。
(5)誤り
ワンポイント解説「1.変圧器の等価回路(一次換算)と鉄損及び銅損」の通り,変圧器の等価回路において,励磁回路は励磁コンダクタンスと励磁サセプタンスで構成され,両者を合わせて励磁アドミタンスといいます。励磁コンダクタンスで発生する損失は鉄損に対応し,励磁サセプタンスに流れる電流は磁化電流に対応しています。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは