【問題】
【難易度】★★★★☆(やや難しい)
図は直流昇圧チョッパ回路であり,スイッチングの周期を\( \ T \ \mathrm {[s]} \ \)とし,その中での動作を考える。ただし,直流電源\( \ \mathrm {E} \ \)の電圧を\( \ E_{0} \ \mathrm {[V]} \ \)とし,コンデンサ\( \ \mathrm {C} \ \)の容量は十分に大きく出力電圧\( \ E_{1} \ \mathrm {[V]} \ \)は一定とみなせるものとする。
半導体スイッチ\( \ \mathrm {S} \ \)がオンの期間\( \ T_{\mathrm {on}} \ \mathrm {[s]} \ \)では,\( \ \mathrm {E}-リアクトル\mathrm {L}-\mathrm {S}-\mathrm {E} \ \)の経路と\( \ \mathrm {C}-負荷\mathrm {R}-\mathrm {C} \ \)の経路の二つで電流が流れ,このときに\( \ \mathrm {L} \ \)に蓄えられるエネルギーが増加する。\( \ \mathrm {S} \ \)がオフの期間\( \ T_{\mathrm {off}} \ \mathrm {[s]} \ \)では,\( \ \mathrm {E}-\mathrm {L}-ダイオード\mathrm {D}-\left( \mathrm {C}と\mathrm {R}の並列回路\right) -\mathrm {E} \ \)の経路で電流が流れ,\( \ \mathrm {L} \ \)に蓄えられたエネルギーが出力側に放出される。次の(a)及び(b)の問に答えよ。
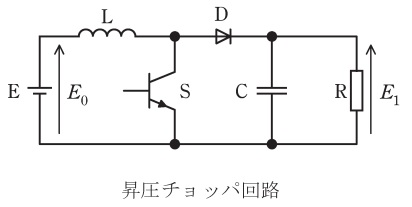
(a) この動作において,\( \ \mathrm {L} \ \)の磁束を増加させる電圧時間積は\( \ \fbox { (ア) } \ \)であり,磁束を減少させる電圧時間積は\( \ \fbox { (イ) } \ \)である。定常状態では,増加する磁束と減少する磁束が等しいとおけるので,入力電圧と出力電圧の関係を求めることができる。
上記の記述中の空白箇所(ア)及び(イ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccc}
& (ア) & (イ) \\
\hline
(1) & E_{0}\cdot T_{\mathrm {on}} & \left( E_{1}-E_{0}\right) \cdot T_{\mathrm {off}} \\
\hline
(2) & E_{0}\cdot T_{\mathrm {on}} & E_{1} \cdot T_{\mathrm {off}} \\
\hline
(3) & E_{0}\cdot T & E_{1} \cdot T_{\mathrm {off}} \\
\hline
(4) & \left( E_{0}-E_{1}\right) \cdot T_{\mathrm {on}} & \left( E_{1}-E_{0}\right) \cdot T_{\mathrm {off}} \\
\hline
(5) & \left( E_{0}-E_{1}\right) \cdot T_{\mathrm {on}} & \left( E_{1}-E_{0}\right) \cdot T \\
\hline
\end{array}
\]
(b) 入力電圧\( \ E_{0}=100 \ \mathrm {V} \ \),通流率\( \ \alpha =0.2 \ \)のときに,出力電圧\( \ E_{1} \ \)の値\( \ \mathrm {[V]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 80 \ \) (2) \( \ 125 \ \) (3) \( \ 200 \ \) (4) \( \ 400 \ \) (5) \( \ 500 \ \)
【ワンポイント解説】
昇圧チョッパに関する問題です。(a)はパワーエレクトロニクスのメカニズムに関する問題,(b)は通流率から出力電圧を求める問題です。昇圧チョッパのメカニズムを理解するためには微分積分の知識が必要となるので,基本的には暗記する方が良いと思います。
1.昇圧チョッパ
スイッチ\( \ \mathrm {S} \ \)が\( \ \mathrm {ON} \ \)時はリアクトル\( \ \mathrm {L} \ \)にエネルギー\( \ EIT_{\mathrm {on}} \ \)が蓄えられ,スイッチ\( \ \mathrm {OFF} \ \)時はリアクトル\( \ \mathrm {L} \ \)に蓄えられたエネルギー\( \ \displaystyle L\frac {\mathrm {d}i}{\mathrm {d}t}IT_{\mathrm {off}} \ \)が放出されます。定常状態では蓄えられるエネルギーと放出するエネルギーが等しいので,
\[
\begin{eqnarray}
EIT_{\mathrm {on}}&=&L\frac {\mathrm {d}i}{\mathrm {d}t}IT_{\mathrm {off}} \\[ 5pt ]
ET_{\mathrm {on}}&=&L\frac {\mathrm {d}i}{\mathrm {d}t}T_{\mathrm {off}} \\[ 5pt ]
L\frac {\mathrm {d}i}{\mathrm {d}t}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}E \\[ 5pt ]
\end{eqnarray}
\]
となります。また回路方程式は,
\[
\begin{eqnarray}
E+L\frac {\mathrm {d}i}{\mathrm {d}t}&=&E_{1} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
E+L\frac {\mathrm {d}i}{\mathrm {d}t}&=&E_{\mathrm {1}} \\[ 5pt ]
E+\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}E&=&E_{\mathrm {1}} \\[ 5pt ]
E_{\mathrm {1}}&=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}E \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.通流率\( \ \alpha \ \)
問題図の回路でトランジスタが\( \ \mathrm {ON} \ \)した時間を\( \ T_{\mathrm {ON}} \ \),トランジスタが\( \ \mathrm {OFF} \ \)した時間を\( \ T_{\mathrm {OFF}} \ \)とすると,通流率\( \ \alpha \ \)は,
\[
\begin{eqnarray}
\alpha &=&\frac {T_{\mathrm {ON}}}{T_{\mathrm {ON}}+ T_{\mathrm {OFF}}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【関連する「電気の神髄」記事】
【解答】
(a)解答:(1)
スイッチ\( \ \mathrm {S} \ \)が\( \ \mathrm {ON} \ \)の時は,\( \ \mathrm {E}-リアクトル\mathrm {L}-\mathrm {S}-\mathrm {E} \ \)の経路と\( \ \mathrm {C}-負荷\mathrm {R}-\mathrm {C} \ \)の経路の二つで電流が流れるので,\( \ \mathrm {L} \ \)には電源電圧が直接蓄えられる。したがって,その電圧時間積は,
\[
\begin{eqnarray}
E_{\mathrm {0}}T_{\mathrm {on}} \\[ 5pt ]
\end{eqnarray}
\]
となる。一方,スイッチ\( \ \mathrm {S} \ \)が\( \ \mathrm {OFF} \ \)の時は,\( \ \mathrm {E}-\mathrm {L}-ダイオード\mathrm {D}-\left( \mathrm {C}と\mathrm {R}の並列回路\right) -\mathrm {E} \ \)の経路で電流が流れ,\( \ \mathrm {L} \ \)を基準とすると\( \ \mathrm {L} \ \)から,\( \ E_{1}-E_{0} \ \)でエネルギーが放出される。したがって,その時間積は,
\[
\begin{eqnarray}
\left( E_{1}-E_{\mathrm {0}}\right) T_{\mathrm {off}} \\[ 5pt ]
\end{eqnarray}
\]
となる。
(b)解答:(2)
\( \ \mathrm {ON} \ \)の時の時間積と\( \ \mathrm {OFF} \ \)の時の時間積は等しいので,
\[
\begin{eqnarray}
E_{\mathrm {0}}T_{\mathrm {on}} &=&\left( E_{1}-E_{\mathrm {0}}\right) T_{\mathrm {off}} ・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「2.通流率\( \ \alpha \ \)」の通り,
\[
\begin{eqnarray}
\alpha &=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+ T_{\mathrm {off}}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,これを整理すると,
\[
\begin{eqnarray}
T_{\mathrm {on}} &=&\alpha \left( T_{\mathrm {on}}+ T_{\mathrm {off}}\right) \\[ 5pt ]
T_{\mathrm {on}} &=&\alpha T_{\mathrm {on}}+\alpha T_{\mathrm {off}} \\[ 5pt ]
\left( 1-\alpha \right) T_{\mathrm {on}} &=&\alpha T_{\mathrm {off}} \\[ 5pt ]
T_{\mathrm {on}} &=&\frac {\alpha }{1-\alpha }T_{\mathrm {off}} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,これを①に代入して整理すると
\[
\begin{eqnarray}
E_{\mathrm {0}}\frac {\alpha }{1-\alpha }T_{\mathrm {off}} &=&\left( E_{1}-E_{\mathrm {0}}\right) T_{\mathrm {off}} \\[ 5pt ]
E_{\mathrm {0}}\frac {\alpha }{1-\alpha } &=& E_{1}-E_{\mathrm {0}} \\[ 5pt ]
E_{1}&=& E_{\mathrm {0}}\frac {\alpha }{1-\alpha }+E_{\mathrm {0}} \\[ 5pt ]
&=& \frac {1}{1-\alpha } E_{\mathrm {0}} \\[ 5pt ]
\end{eqnarray}
\]
となり,各値を代入すると,
\[
\begin{eqnarray}
E_{1}&=& \frac {1}{1-0.2} \times 100 \\[ 5pt ]
&=& 125 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは