《機械》〈誘導機〉[R05下:問15]電動機の滑り周波数と周波数特性に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

定格出力\( \ 15 \ \mathrm {kW} \ \)，定格周波数\( \ 60 \ \mathrm {Hz} \ \)，\( \ 4 \ \)極の三相誘導電動機があり，トルク一定の負荷を負って運転している。この電動機について，次の(a)及び(b)の問に答えよ。

(a)　定格回転速度\( \ 1 \ 746 \ \mathrm {{min}^{-1}} \ \)で運転しているときの滑り周波数の値\( \ \mathrm {[Hz]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 1.50 \ \)　　(2)　\( \ 1.80 \ \)　　(3)　\( \ 1.86 \ \)　　(4)　\( \ 2.10 \ \)　　(5)　\( \ 2.17 \ \)

(b)　インバータにより一次周波数制御を行って，一次周波数を\( \ 40 \ \mathrm {Hz} \ \)としたときの回転速度\( \ \mathrm {[{min}^{-1}]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。
　ただし，滑り周波数は一次周波数にかかわらず常に一定とする。

　(1)　\( \ 1 \ 146 \ \)　　(2)　\( \ 1 \ 164 \ \)　　(3)　\( \ 1 \ 433 \ \)　　(4)　\( \ 1 \ 455 \ \)　(5)　\( \ 1 \ 719 \ \)

【ワンポイント解説】

誘導電動機の滑り周波数と，一次周波数を変化したときの回転数変化に関する問題です。
求めるのが滑りではなく滑り周波数，周波数を変化させる等誘導電動機の問題としては少し捻った問題となりますが，内容は理解してしまえばそれほど難解ではありませんので，ここで理解するようにしましょう。
本問は平成16年問15からの再出題となります

1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \)，電源の周波数が\( \ f \ \mathrm {[Hz]} \ \)の時，同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は，
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ] \end{eqnarray}
\] となります。

2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)，回転子の回転速度が\( \ N \ \mathrm {[{min}^{-1}]} \ \)である時，誘導機の滑り\( \ s \ \)は，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] と定義されます。これを整理すると，
\[
\begin{eqnarray}
sN_{\mathrm {s}} &=&N_{\mathrm {s}}-N \\[ 5pt ] N &=&N_{\mathrm {s}}-sN_{\mathrm {s}} \\[ 5pt ] &=&\left( 1-s \right) N_{\mathrm {s}} \\[ 5pt ] \end{eqnarray}
\] と同期速度から回転速度が導出できます。

3.滑り周波数
誘導電動機の二次側（回転子）に発生する周波数をいい，一次側（固定子）の周波数を\( \ f_{1} \ \mathrm {[Hz]} \ \)，滑りを\( \ s \ \)とすると，滑り周波数\( \ f_{2} \ \mathrm {[Hz]} \ \)は，
\[
\begin{eqnarray}
f_{2}&=&sf_{1} \\[ 5pt ] \end{eqnarray}
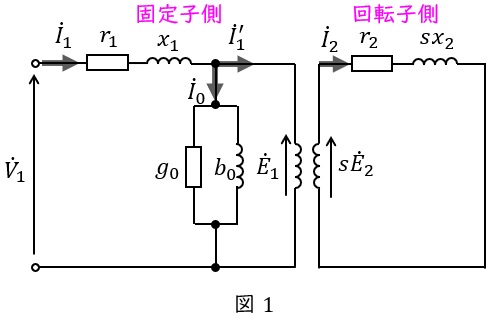
\] となります。これは二次側回路の誘導起電力にも関係し，二次の誘導起電力は\( \ sE_{2} \ \mathrm {[V]} \ \)となり，等価回路は図1のようになります。
（電動機の回転子が回転磁界の中で回転しているイメージを持つとわかりやすいかと思います。）

【解答】

(a)解答：(2)
三相誘導起電力の同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は，定格周波数\( \ f_{1}=60 \ \mathrm {[Hz]} \ \)，極数\( \ p=4 \ \)であるから，ワンポイント解説「1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)」の通り，
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f_{1}}{p} \\[ 5pt ] &=&\frac {120\times 60}{4} \\[ 5pt ] &=&1 \ 800 \ \mathrm {[{min}^{-1}]} \\[ 5pt ] \end{eqnarray}
\] となるので，滑り\( \ s \ \)は，ワンポイント解説「2.誘導機の滑り\( \ s \ \)」の通り，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ] &=&\frac {1 \ 800-1 \ 746}{1 \ 800} \\[ 5pt ] &=&0.03 \\[ 5pt ] \end{eqnarray}
\] となる。したがって，滑り周波数\( \ f_{2} \ \mathrm {[Hz]} \ \)は，ワンポイント解説「3.滑り周波数」の通り，
\[
\begin{eqnarray}
f_{2}&=&sf_{1} \\[ 5pt ] &=&0.03\times 60 \\[ 5pt ] &=&1.80 \ \mathrm {[Hz]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(1)
問題文より，滑り周波数の値は一定であるので，このときの滑り\( \ s^{\prime } \ \)は一次周波数\( \ f_{1}^{\prime }=40 \ \mathrm {[Hz]} \ \)であるから，
\[
\begin{eqnarray}
f_{2}&=&s^{\prime }f_{1}^{\prime } \\[ 5pt ] s^{\prime }&=&\frac {f_{2}}{f_{1}^{\prime }} \\[ 5pt ] &=&\frac {1.80}{40} \\[ 5pt ] &=&0.045 \\[ 5pt ] \end{eqnarray}
\] となり，同期速度\( \ N_{\mathrm {s}}^{\prime } \ \mathrm {[{min}^{-1}]} \ \)は，ワンポイント解説「1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)」の通り，
\[
\begin{eqnarray}
N_{\mathrm {s}}^{\prime } &=&\frac {120f_{1}^{\prime }}{p} \\[ 5pt ] &=&\frac {120\times 40}{4} \\[ 5pt ] &=&1 \ 200 \ \mathrm {[{min}^{-1}]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，このときの回転速度\( \ N^{\prime } \ \mathrm {[{min}^{-1}]} \ \)は，ワンポイント解説「2.誘導機の滑り\( \ s \ \)」の通り，
\[
\begin{eqnarray}
N^{\prime } &=&\left( 1-s^{\prime } \right) N_{\mathrm {s}}^{\prime } \\[ 5pt ] &=&\left( 1-0.045 \right) \times 1 \ 200 \\[ 5pt ] &=&1 \ 146 \ \mathrm {[{min}^{-1}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。