《機械》〈照明〉[R05下:問17]２つの点光源を設置した際の水平面照度に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

どの方向にも光度が等しい均等放射の点光源がある。この点光源の全光束は\( \ 15000 \ \mathrm {lm} \ \)である。この点光源二つ\( \ \left( \mathrm {A}\right. \ \)及び\( \ \left.\mathrm {B}\right) \ \)を屋外で図のように配置した。地面から点光源までの高さはいずれも\( \ 4 \ \mathrm {m} \ \)であり，\( \ \mathrm {A} \ \)と\( \ \mathrm {B} \ \)との距離は\( \ 6 \ \mathrm {m} \ \)である。次の(a)及び(b)の問に答えよ。ただし，考える空間には，\( \ \mathrm {A} \ \)及び\( \ \mathrm {B} \ \)以外に光源はなく，地面や周囲などからの反射光の影響もないものとする。

(a)　図において，点光源\( \ \mathrm {A} \ \)のみを点灯した。\( \ \mathrm {A} \ \)の直下の地面\( \ \mathrm {A}^{\prime } \ \)点における水平面照度の値\( \ \mathrm {[lx]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 56 \ \)　　(2)　\( \ 75 \ \)　　(3)　\( \ 100 \ \)　　(4)　\( \ 149 \ \)　　(5)　\( \ 299 \ \)

(b)　図において，点光源\( \ \mathrm {A} \ \)を点灯させたまま，点光源\( \ \mathrm {B} \ \)も点灯した。このとき，地面\( \ \mathrm {C} \ \)点における水平面照度の値\( \ \mathrm {[lx]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 46 \ \)　　(2)　\( \ 57 \ \)　　(3)　\( \ 76 \ \)　　(4)　\( \ 96 \ \)　　(5)　\( \ 153 \ \)

【ワンポイント解説】

２つの点光源を設置した際の水平面照度を求める問題です。
いずれも機械科目の照明分野としては出題されやすい内容で，比較的パターンも決まっている問題ですので，ぜひマスターし得点源とするようにして下さい。
本問は平成30年問17からの再出題となります。

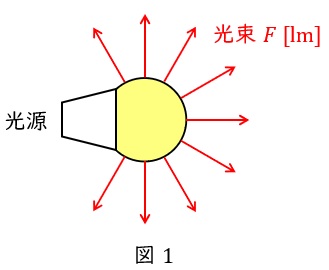
1.光束\( \ F \ \)
光源から出る可視光の量（エネルギー）で，単位は\( \ \mathrm {[lm]} \ \)となります。
電磁気の分野の電束に似たようなイメージで良いです。

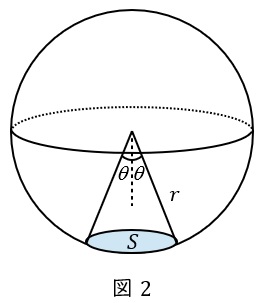
2.立体角の定義
図2のように球体があり，半径\( \ r \ \mathrm {[m]} \ \)の錐体が球面を切り取った時の面積を\( \ S \ \mathrm {[m^{2}]} \ \)とすると，立体角\( \ \omega \ \mathrm {[sr]} \ \)は，
\[
\begin{eqnarray}
\omega &=&\frac {S}{r^{2}} \\[ 5pt ] \end{eqnarray}
\] であり，平面角\( \ \theta \ \mathrm {[rad]} \ \)で表すと，
\[
\begin{eqnarray}
\omega &=&2\pi \left( 1-\cos \theta \right) \\[ 5pt ] \end{eqnarray}
\] となります。球全体の立体角は\( \ \theta = \pi \ \)の時であり，\( \ \omega =4\pi \ \)となります。

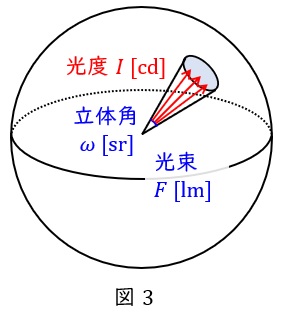
3.光度\( \ I \ \)
ある方向に向かう光束\( \ F \ \mathrm {[lm]} \ \)を立体角\( \ \omega \ \mathrm {[sr]} \ \)で割ったもので，光度\( \ I \ \mathrm {[cd]} \ \)を式で表すと，
\[
\begin{eqnarray}
I &=&\frac {F}{\omega } \\[ 5pt ] \end{eqnarray}
\] となります。

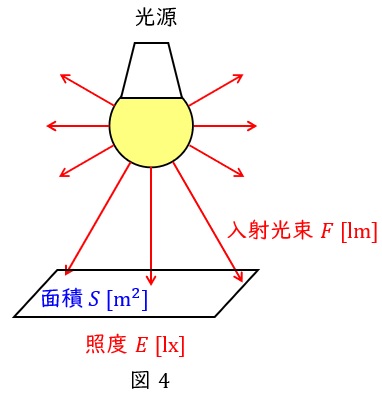
4.照度\( \ E \ \)
図4のように，光源からある方向へ向かう光度が\( \ I \ \mathrm {[cd]} \ \)であるとき，光源からの距離\( \ l \ \mathrm {[m]} \ \)離れた垂直面の照度\( \ E \ \mathrm {[lx]} \ \)は，
\[
\begin{eqnarray}
E&=&\frac {I}{l^{2}} \\[ 5pt ] \end{eqnarray}
\] で求められます。このように，一般に物理量が\( \ 2 \ \)乗に反比例する法則を逆\( \ 2 \ \)乗の法則といいます。

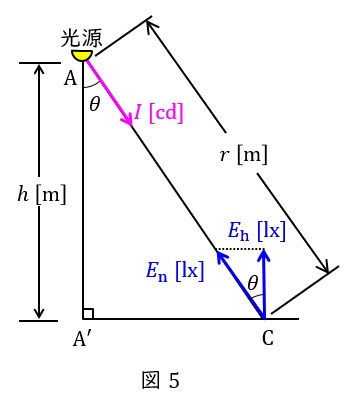
5.水平面照度\( \ E_{\mathrm {h}} \ \)
図5のように，点光源から光度\( \ I \ \mathrm {[cd]} \ \)で\( \ \mathrm {C} \ \)点に向かって光が照射されているとき，法線照度\( \ E_{\mathrm {n}} \ \mathrm {[lx]} \ \)は，
\[
\begin{eqnarray}
E_{\mathrm {n}} &=&\frac {I}{r^{2}} \\[ 5pt ] \end{eqnarray}
\] で表され，水平面照度\( \ E_{\mathrm {h}} \ \mathrm {[lx]} \ \)は，\( \ E_{\mathrm {n}} \ \mathrm {[lx]} \ \)の余弦であるから，
\[
\begin{eqnarray}
E_{\mathrm {h}} &=&E_{\mathrm {n}}\cos \theta \\[ 5pt ] &=&\frac {I}{r^{2}}\cdot \frac {h}{r} \\[ 5pt ] &=&\frac {hI}{r^{3}}
\end{eqnarray}
\] となります。

【解答】

(a)解答：(2)
点光源\( \ \mathrm {A} \ \)から\( \ \mathrm {A}^{\prime } \ \)に向かう光度\( \ I \ \mathrm {[cd]} \ \)は，ワンポイント解説「2.立体角の定義」及び「3.光度\( \ I \ \)」の通り，
\[
\begin{eqnarray}
I &=&\frac {F}{\omega } \\[ 5pt ] &=&\frac {15 \ 000}{4\pi } \\[ 5pt ] &≒&1 \ 194 \ \mathrm {[cd]} \\[ 5pt ] \end{eqnarray}
\] であるから，\( \ \mathrm {A}^{\prime } \ \)点における水平面照度\( \ E_{\mathrm {h1}} \ \mathrm {[lx]} \ \)は，ワンポイント解説「5.水平面照度\( \ E_{\mathrm {h}} \ \)」の通り，
\[
\begin{eqnarray}
E_{\mathrm {h1}} &=&\frac {I}{h^{2}} \\[ 5pt ] &=&\frac {1 \ 194}{4^{2}} \\[ 5pt ] &≒&74.63　→　75 \ \mathrm {[lx]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
点光源\( \ \mathrm {A} \ \)と\( \ \mathrm {C} \ \)点との距離\( \ r \ \mathrm {[m]} \ \)は，三平方の定理より，
\[
\begin{eqnarray}
r &=&\sqrt {3^{2}+4^{2}} \\[ 5pt ] &=&5 \ \mathrm {[m]} \\[ 5pt ] \end{eqnarray}
\] となるので，点光源\( \ \mathrm {A} \ \)による\( \ \mathrm {C} \ \)点における法線照度\( \ E_{\mathrm {n}} \ \mathrm {[lx]} \ \)は，ワンポイント解説「5.水平面照度\( \ E_{\mathrm {h}} \ \)」の通り，
\[
\begin{eqnarray}
E_{\mathrm {n}} &=&\frac {I}{r^{2}} \\[ 5pt ] &=&\frac {1 \ 194}{5^{2}} \\[ 5pt ] &=&47.76 \ \mathrm {[lx]} \\[ 5pt ] \end{eqnarray}
\] となる。よって、点光源\( \ \mathrm {A} \ \)による\( \ \mathrm {C} \ \)点における水平面照度\( \ E_{\mathrm {h2}} \ \mathrm {[lx]} \ \)は，ワンポイント解説「5.水平面照度\( \ E_{\mathrm {h}} \ \)」の通り，
\[
\begin{eqnarray}
E_{\mathrm {h2}} &=&E_{\mathrm {n}}\cos \theta \\[ 5pt ] &=&47.76\times \frac {4}{5} \\[ 5pt ] &≒&38.21 \ \mathrm {[lx]} \\[ 5pt ] \end{eqnarray}
\] となり，点光源\( \ \mathrm {B} \ \)からも同照度が求められるので，求める水平面照度\( \ E_{\mathrm {h}} \ \mathrm {[lx]} \ \)は，
\[
\begin{eqnarray}
E_{\mathrm {h}} &=&2\times 38.21 \\[ 5pt ] &=&76.42　→　76 \ \mathrm {[lx]} \\[ 5pt ] \end{eqnarray}
\] と求められる。