《機械》〈自動制御〉[R05下:問18]ブロック線図の周波数伝達関数の導出に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

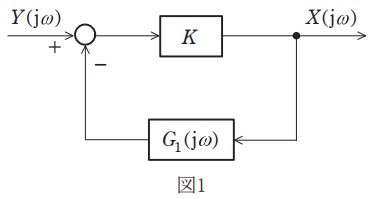
図1は，調節計の演算回路などによく用いられるブロック線図を示す。次の(a)及び(b)の問に答えよ。

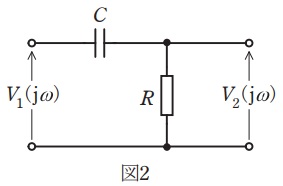
(a)　図2は，図1のブロック\( \ G_{1}\left( \mathrm {j}\omega \right) \ \)の詳細を示し，静電容量\( \ C \ \mathrm {[F]} \ \)と抵抗\( \ R \ \mathrm {[\Omega ]} \ \)からなる回路を示す。この回路の入力量\( \ V_{1}\left( \mathrm {j}\omega \right) \ \)に対する出力量\( \ V_{2}\left( \mathrm {j}\omega \right) \ \)の周波数伝達関数\( \ \displaystyle G_{1}\left( \mathrm {j}\omega \right) =\frac {V_{2}\left( \mathrm {j}\omega \right) }{V_{1}\left( \mathrm {j}\omega \right) } \ \)を表す式として，正しいものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ \displaystyle \frac {1}{CR+\mathrm {j}\omega } \ \)　　(2)　\( \ \displaystyle \frac {1}{1+\mathrm {j}\omega CR} \ \)　　(3)　\( \ \displaystyle \frac {CR}{CR+\mathrm {j}\omega } \ \)　　
　(4)　\( \ \displaystyle \frac {CR}{1+\mathrm {j}\omega CR} \ \)　　(5)　\( \ \displaystyle \frac {\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR} \ \)

(b)　図1のブロック線図において，閉ループ周波数伝達関数\( \ \displaystyle G\left( \mathrm {j}\omega \right) =\frac {X\left( \mathrm {j}\omega \right) }{Y\left( \mathrm {j}\omega \right) } \ \)で，ゲイン\( \ K \ \)が非常に大きな場合の近似式として，正しいものを次の(1)～(5)のうちから一つ選べ。
　なお，この近似式が成立する場合，この演算回路は比例プラス積分要素と呼ばれる。

　(1)　\( \ 1+\mathrm {j}\omega CR \ \)　　(2)　\( \ \displaystyle 1+\frac {CR}{\mathrm {j}\omega } \ \)　　(3)　\( \ \displaystyle 1+\frac {1}{\mathrm {j}\omega CR} \ \)　　
　(4)　\( \ \displaystyle \frac {1}{1+\mathrm {j}\omega CR} \ \)　　(5)　\( \ \displaystyle \frac {1+CR}{\mathrm {j}\omega CR} \ \)

【ワンポイント解説】

近似を用いたブロック線図の周波数伝達関数の導出に関する問題です。
(b)が数学を学習されているかどうかで解ける解けないが分かれる問題かと思います。分数を作って零を作るという方法は極限の数学においてよく使う手法となります。
本問は平成20年問17からの再出題となります。

1.ブロック線図の考え方
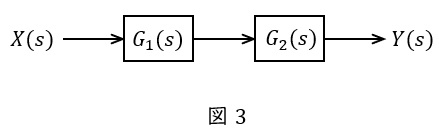
①直列
図3のような伝達関数\( \ G_{1}(s) \ \)，\( \ G_{2}(s) \ \)が与えられているとき，全体の伝達関数\( \ G(s) \ \)は，
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)G_{2}(s) \\[ 5pt ] \end{eqnarray}
\] となります。

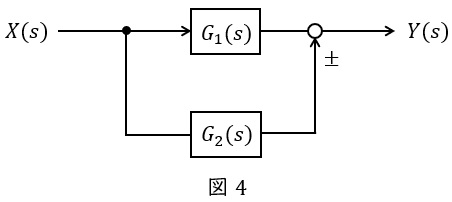
②並列
図4のような伝達関数\( \ G_{1}(s) \ \)，\( \ G_{2}(s) \ \)が与えられているとき，全体の伝達関数\( \ G(s) \ \)は，
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)±G_{2}(s) \\[ 5pt ] \end{eqnarray}
\] となります。

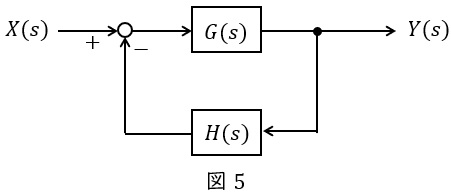
③フィードバック
図5のような\( \ G(s) \ \)，\( \ H(s) \ \)が与えられているとき，全体の伝達関数\( \ W(s) \ \)は，
\[
\begin{eqnarray}
Y(s)&=&\left\{ X(s) -H(s)Y(s) \right\} G(s) \\[ 5pt ] Y(s)&=&G(s)X(s) -G(s)H(s)Y(s) \\[ 5pt ] Y(s)+G(s)H(s)Y(s) &=&G(s)X(s) \\[ 5pt ] \left\{ 1+G(s)H(s)\right\} Y(s) &=&G(s)X(s) \\[ 5pt ] \frac {Y(s)}{X(s)}&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ] W(s)&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(5)
分圧の法則より，
\[
\begin{eqnarray}
V_{2}\left( \mathrm {j}\omega \right) &=&\frac {R}{\displaystyle R+\frac {1}{\mathrm {j}\omega C}}V_{1}\left( \mathrm {j}\omega \right) \\[ 5pt ] \frac {V_{2}\left( \mathrm {j}\omega \right) }{V_{1}\left( \mathrm {j}\omega \right) }&=&\frac {R}{\displaystyle R+\frac {1}{\mathrm {j}\omega C}} \\[ 5pt ] G_{1}\left( \mathrm {j}\omega \right) &=&\frac {R}{\displaystyle \frac {1+\mathrm {j}\omega CR}{\mathrm {j}\omega C}} \\[ 5pt ] &=&\frac {\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(3)
図1の伝達関数\( \ \displaystyle G\left( \mathrm {j}\omega \right) \ \)は，ワンポイント解説「1.ブロック線図の考え方」の通り，
\[
\begin{eqnarray}
G\left( \mathrm {j}\omega \right) &=&\frac {K}{1+KG_{1}\left( \mathrm {j}\omega \right) } \\[ 5pt ] &=&\frac {1}{\displaystyle \frac {1}{K}+G_{1}\left( \mathrm {j}\omega \right) } \\[ 5pt ] \end{eqnarray}
\] となり，\( \ K \ \)が非常に大きいとき，\( \ \displaystyle \frac {1}{K} \ \)は無視できるから，
\[
\begin{eqnarray}
G\left( \mathrm {j}\omega \right) &≈&\frac {1}{G_{1}\left( \mathrm {j}\omega \right) } \\[ 5pt ] &=&\frac {1}{\displaystyle \frac {\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR}} \\[ 5pt ] &=&\frac {1+\mathrm {j}\omega CR}{\mathrm {j}\omega CR} \\[ 5pt ] &=&1+\frac {1}{\mathrm {j}\omega CR} \\[ 5pt ] \end{eqnarray}
\] と求められる。