Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
図のようなブロック線図で示す制御系がある。出力信号\( \ C \left( \mathrm {j}\omega \right) \ \)の入力信号\( \ R \left( \mathrm {j}\omega \right) \ \)に対する比,すなわち\(\displaystyle \frac {C \left( \mathrm {j}\omega \right) }{R \left( \mathrm {j}\omega \right) }\)を示す式として,正しいものを次の(1)~(5)のうちから一つ選べ。
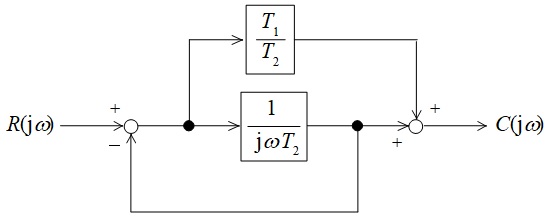
(1) \(\displaystyle \frac {T_{1}+\mathrm {j}\omega }{T_{2}+\mathrm {j}\omega }\) (2) \(\displaystyle \frac {T_{2}+\mathrm {j}\omega }{T_{1}+\mathrm {j}\omega }\) (3) \(\displaystyle \frac {\mathrm {j}\omega T_{1} }{1+\mathrm {j}\omega T_{2} }\)
(4) \(\displaystyle \frac {1+\mathrm {j}\omega T_{1} }{1+\mathrm {j}\omega T_{2} }\) (5) \(\displaystyle \frac {1+\mathrm {j}\omega \displaystyle \frac {T_{1}}{T_{2}} }{1+\mathrm {j}\omega T_{2} }\)
【ワンポイント解説】
ブロック線図と伝達関数に関する問題です。公式や等価変換表を暗記しても良いですが,なぜそうなるかを理解し,問題を解きながら徐々に覚えていくのが良いと思います。別解のように手計算で導出可能な場合も多いので,そのように解いても良いと思います。
【解答】
解答:(4)
問題の回路を等価変換すると図1のようになる。
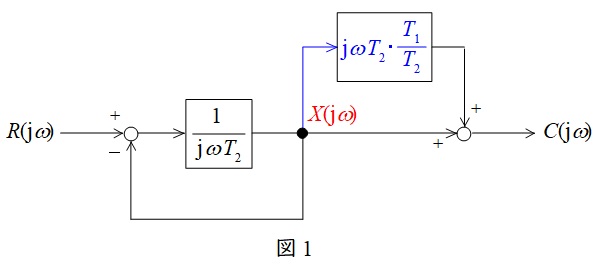
図1より,中間部の信号を\( \ X \left( \mathrm {j}\omega \right) \ \)とすると,
\[
\begin{eqnarray}
X \left( \mathrm {j}\omega \right) &=&\frac {\displaystyle \frac {1}{\mathrm {j}\omega T_{2}}}{1+\displaystyle \frac {1}{\mathrm {j}\omega T_{2}}}R \left( \mathrm {j}\omega \right) \\[ 5pt ]
&=&\frac {1}{1+\mathrm {j}\omega T_{2}}R \left( \mathrm {j}\omega \right) \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
C \left( \mathrm {j}\omega \right) &=&\mathrm {j}\omega T_{2}\cdot \frac {T_{1}}{T_{2}}X \left( \mathrm {j}\omega \right) +X \left( \mathrm {j}\omega \right) \\[ 5pt ]
&=&\left( 1+\mathrm {j}\omega T_{1}\right) X \left( \mathrm {j}\omega \right) \\[ 5pt ]
&=&\left( 1+\mathrm {j}\omega T_{1}\right) \frac {1}{1+\mathrm {j}\omega T_{2}}R \left( \mathrm {j}\omega \right) \\[ 5pt ]
&=&\frac {1+\mathrm {j}\omega T_{1}}{1+\mathrm {j}\omega T_{2}}R \left( \mathrm {j}\omega \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(別解)
問題図の中間部の信号を図2のように置く。
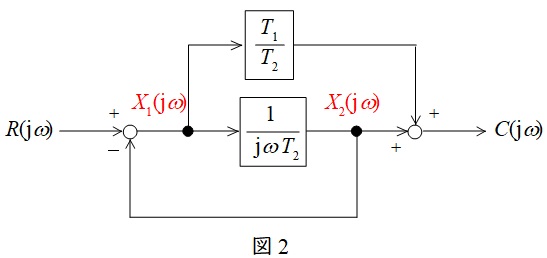
図2より,
\[
\begin{eqnarray}
R \left( \mathrm {j}\omega \right) -X_{2} \left( \mathrm {j}\omega \right) &=&X_{1} \left( \mathrm {j}\omega \right) &・・・・・①& \\[ 5pt ]
X_{2} \left( \mathrm {j}\omega \right) &=&\frac {1}{\mathrm {j}\omega T_{2}} X_{1} \left( \mathrm {j}\omega \right) &・・・・・②& \\[ 5pt ]
C \left( \mathrm {j}\omega \right) &=&\frac {T_{1}}{T_{2}}X_{1} \left( \mathrm {j}\omega \right) +X_{2} \left( \mathrm {j}\omega \right) &・・・・・③& \\[ 5pt ]
\end{eqnarray}
\]
となる。\(②\)より,
\[
\begin{eqnarray}
X_{1} \left( \mathrm {j}\omega \right) &=&\mathrm {j}\omega T_{2}X_{2} \left( \mathrm {j}\omega \right) &・・・・・②^{\prime }& \\[ 5pt ] \\[ 5pt ]
\end{eqnarray}
\]
であるから,これを\(①\)に代入すると,
\[
\begin{eqnarray}
R \left( \mathrm {j}\omega \right) -X_{2} \left( \mathrm {j}\omega \right) &=&\mathrm {j}\omega T_{2}X_{2} \left( \mathrm {j}\omega \right) \\[ 5pt ]
R \left( \mathrm {j}\omega \right) &=&\left( 1 +\mathrm {j}\omega T_{2}\right) X_{2} \left( \mathrm {j}\omega \right) \\[ 5pt ]
X_{2} \left( \mathrm {j}\omega \right) &=&\frac {1}{1 +\mathrm {j}\omega T_{2}}R \left( \mathrm {j}\omega \right) &・・・・・④& \\[ 5pt ]
\end{eqnarray}
\]
となる。\(②^{\prime }\)及び\(④\)を\(③\)に代入すると,
\[
\begin{eqnarray}
C \left( \mathrm {j}\omega \right) &=&\frac {T_{1}}{T_{2}}X_{1} \left( \mathrm {j}\omega \right) +X_{2} \left( \mathrm {j}\omega \right) \\[ 5pt ]
&=&\frac {T_{1}}{T_{2}}\cdot \mathrm {j}\omega T_{2}X_{2} \left( \mathrm {j}\omega \right) +X_{2} \left( \mathrm {j}\omega \right) \\[ 5pt ]
&=& \mathrm {j}\omega T_{1}X_{2} \left( \mathrm {j}\omega \right) +X_{2} \left( \mathrm {j}\omega \right) \\[ 5pt ]
&=& \left( 1+ \mathrm {j}\omega T_{1}\right) X_{2} \left( \mathrm {j}\omega \right) \\[ 5pt ]
&=& \left( 1+ \mathrm {j}\omega T_{1}\right) \cdot \frac {1}{1 +\mathrm {j}\omega T_{2}}R \left( \mathrm {j}\omega \right) \\[ 5pt ]
&=&\frac {1+\mathrm {j}\omega T_{1}}{1+\mathrm {j}\omega T_{2}}R \left( \mathrm {j}\omega \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは