《機械》〈直流機〉[R05下:問2]界磁に永久磁石を用いた小形直流電動機の特性に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

界磁に永久磁石を用いた小形直流電動機がある。この電動機の電機子に\( \ 12 \ \mathrm {V} \ \)の電圧を加えたところ，無負荷の状態で\( \ 3 \ 000 \ \mathrm {min}^{-1} \ \)で回転した。この電圧を維持したまま負荷を与えて，\( \ 2 \ \mathrm {A} \ \)の電機子電流を流したところ，損失が\( \ 3 \ \mathrm {W} \ \)発生した。この時の回転数\( \ [\mathrm {min}^{-1}] \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，ブラシの接触による電圧降下及び電機子反作用は無視できるものとし，損失は電機子巻線の銅損しか存在しないものとする。

　(1)　\( \ 2 \ 250 \ \)　　(2)　\( \ 2 \ 625 \ \)　　(3)　\( \ 2 \ 813 \ \)　　 (4)　\( \ 3 \ 000 \ \)　　(5)　\( \ 3 \ 429 \ \)

【ワンポイント解説】

界磁に永久磁石を用いた小形直流電動機に関する問題です。
慣れていないと永久磁石の扱いに戸惑ってしまうかもしれませんが，あまり難しく考えず励磁電流が一定である他励電動機と考えれば良いです。
令和5年上期問2にも永久磁石を用いた電動機の問題が出題されたので，今後の新傾向になるかもしれません。

1.直流他励電動機の等価回路
図1に直流他励電動機の等価回路を示します。図1において，\( \ V \ \mathrm {[V]} \ \)は端子電圧，\( \ E \ \mathrm {[V]} \ \)は逆起電力，\( \ V_{\mathrm {f}} \ \mathrm {[V]} \ \)は界磁電圧，\( \ I_{\mathrm {a}} \ \mathrm {[A]} \ \)は電機子電流，\( \ I_{\mathrm {f}} \ \mathrm {[A]} \ \)は界磁電流，\( \ R_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)は電機子抵抗，\( \ R_{\mathrm {f}} \ \mathrm {[\Omega ]} \ \)は界磁抵抗となります。
他励式の特徴としては，界磁回路が独立しているので，界磁磁束を独立して制御できるという特徴があります。

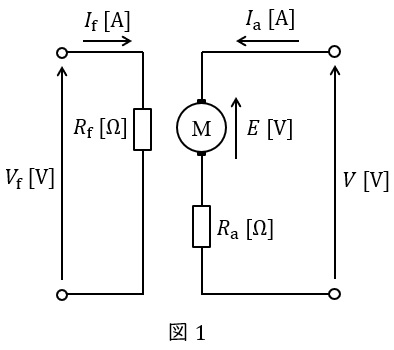
また，上記の等価回路にキルヒホッフの法則を適用すると，以下の関係式が導き出せることが分かります。
\[
\begin{eqnarray}
V &=& E+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] I_{\mathrm {f}} &=& \frac {V_{\mathrm {f}}}{r_{\mathrm {f}}} \\[ 5pt ] \end{eqnarray}
\]

2.直流機の誘導起電力(逆起電力)\( \ E \ \)
磁極の数\( \ p \ \)，電機子導体数\( \ Z \ \)，電機子巻線並列回路数\( \ a \ \)，各極の磁束\( \ \phi \ \mathrm {[Wb]} \ \)，回転速度\( \ N \ \mathrm {[{min}^{-1}]} \ \)とすると，直流機の誘導起電力(逆起電力)\( \ E \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
E &=&\frac {pZ}{60a}\phi N \\[ 5pt ] &=&k_{\mathrm {e}}\phi N \\[ 5pt ] \end{eqnarray}
\] となり，磁束\( \ \phi \ \mathrm {[Wb]} \ \)と回転速度\( \ N \ \mathrm {[{min}^{-1}]} \ \)に比例します。

【解答】

解答：(2)
問題文で与えられている各値を，電機子電圧\( \ V=12 \ \mathrm {[V]} \ \)，無負荷状態での回転速度\( \ N_{0}=3 \ 000 \ \mathrm {[{min}^{-1}]} \ \)，電機子電流\( \ I_{\mathrm {a}} =2 \ \mathrm {[A]} \ \)とおく。
無負荷の状態では電機子電流は\( \ 0 \ \mathrm {A} \ \)と考えれば良いので，誘導起電力\( \ E_{0}=V=12 \ \mathrm {[V]} \ \)となる。
負荷を与えたところ，電機子電流\( \ I_{\mathrm {a}} =2 \ \mathrm {[A]} \ \)で運転し，損失（銅損）が\( \ P_{\mathrm {l}} =3 \ \mathrm {[W]} \ \)なので，電機子巻線抵抗\( \ R_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
R_{\mathrm {a}} &=&\frac {P_{\mathrm {l}}}{{I_{\mathrm {a}}}^{2}} \\[ 5pt ] &=&\frac {3}{2^{2}} \\[ 5pt ] &=&0.75 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，負荷を与えたときの誘導起電力\( \ E \ \mathrm {[V]} \ \)は，ワンポイント解説「1.直流他励電動機の等価回路」の通り，
\[
\begin{eqnarray}
E &=&V-R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] &=&12-0.75\times 2 \\[ 5pt ] &=&10.5 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となり，ワンポイント解説「2.直流機の誘導起電力(逆起電力)\( \ E \ \)」の通り，誘導起電力と回転速度は比例するので，負荷を与えたときの回転速度\( \ N \ \mathrm {[{min}^{-1}]} \ \)は，
\[
\begin{eqnarray}
N &=&\frac {E}{E_{0}}N_{0} \\[ 5pt ] &=&\frac {10.5}{12}\times 3 \ 000 \\[ 5pt ] &=&2 \ 625 \ \mathrm {[{min}^{-1}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。