《機械》〈パワーエレクトロニクス〉[H28:問16]単相サイリスタ全波整流回路に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

純抵抗を負荷とした単相サイリスタ全波整流回路の動作について，次の(a)及び(b)の問に答えよ。

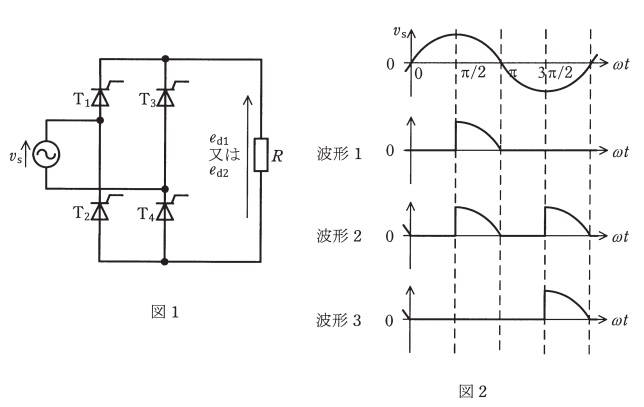
(a)　図1に単相サイリスタ全波整流回路を示す。サイリスタ\( \ \mathrm {T_{1}～T_{4}} \ \)に制御遅れ角\( \ \displaystyle \alpha =\frac {\pi }{2} \ [ \mathrm {rad} ] \ \)でゲート信号を与えて運転しようとしている。\( \ \mathrm {T_{2}} \ \)及び\( \ \mathrm {T_{3}} \ \)のゲート信号は正しく与えられたが，\( \ \mathrm {T_{1}} \ \)及び\( \ \mathrm {T_{4}} \ \)のゲート信号が全く与えられなかった場合の出力電圧波形を\( \ e_{\mathrm {d1}} \ \)とし，正しく\( \ \mathrm {T_{1}～T_{4}} \ \)にゲート信号が与えられた場合の出力電圧波形を\( \ e_{\mathrm {d2}} \ \)とする。図2の波形\( \ 1 \ \)～波形\( \ 3 \ \)から，\( \ e_{\mathrm {d1}} \ \)と\( \ e_{\mathrm {d2}} \ \)の組合せとして正しいものを次の(1)～(5)のうちから一つ選べ。

\[
\begin{array}{ccc}
& 電圧波形 \ e_{\mathrm {d1}} & 電圧波形 \ e_{\mathrm {d1}} \\
\hline
(1) & 波形 \ 1 & 波形 \ 2 \\
\hline
(2) & 波形 \ 2 & 波形 \ 1 \\
\hline
(3) & 波形 \ 2 & 波形 \ 3 \\
\hline
(4) & 波形 \ 3 & 波形 \ 1 \\
\hline
(5) & 波形 \ 3 & 波形 \ 2 \\
\hline
\end{array}
\]

(b)　単相交流電源電圧\( \ v_{\mathrm {s}} \ \)の実効値を\( \ V \ \mathrm {[ V ]} \ \)とする。ゲート信号が正しく与えられた場合の出力電圧波形\( \ e_{\mathrm {d2}} \ \)について，制御遅れ角\( \ \alpha \ \mathrm {[ rad ]} \ \)と出力電圧の平均値\( \ E_{\mathrm {d}} \ \mathrm {[ V ]} \ \)との関係を表す式として，正しいものに最も近いものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{eqnarray}
&(1)&　E_{\mathrm {d}}=0.45V\frac {1+\cos \alpha }{2}　　&(2)&　E_{\mathrm {d}}=0.9V\frac {1+\cos \alpha }{2}　　&(3)&　E_{\mathrm {d}}=V\frac {1+\cos \alpha }{2} \\[ 5pt ] &(4)&　E_{\mathrm {d}}=0.45V\cos \alpha　　&(5)&　E_{\mathrm {d}}=0.9V\cos \alpha　
\end{eqnarray}
\]

【ワンポイント解説】

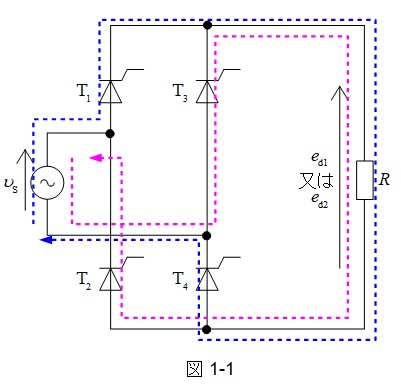
図1-1に示すように，本問のサイリスタは\( \ v_{\mathrm {S}} > 0 \ \)の時，制御遅れ角\( \ \displaystyle \alpha =\frac {\pi }{2} \ \mathrm {[ rad ]} \ \)の後，\( \ \mathrm {T_{1}} \ \)及び\( \ \mathrm {T_{4}} \ \)が導通して\( \ R \ \)に電圧が発生し，\( \ v_{\mathrm {S}} < 0 \ \)の時，\( \ \mathrm {T_{2}} \ \)及び\( \ \mathrm {T_{3}} \ \)が導通して\( \ R \ \)に電圧が発生します。\( \ R \ \)を通る電流の向きは同じなので，電圧も同方向の電圧が発生します。

【関連する「電気の神髄」記事】

　　単相全波整流回路

【解答】

(a)解答：(5)
制御遅れ角\( \ \displaystyle \alpha =\frac {\pi }{2} \ \mathrm {[ rad ]} \ \)であるから，全てのサイリスタが正常動作している場合は波形2となる。\( \ \mathrm {T_{1}} \ \)及び\( \ \mathrm {T_{4}} \ \)のゲート信号が与えられない場合，\( \ v_{\mathrm {S}} > 0 \ \)の時，電圧が一切発生しなくなるので，波形3となる。

(b)解答：(2)
出力される電圧は，周期\( \ \pi \ \)の正弦波形であるから，\( \ v_{\mathrm {S}}=v\sin \omega t \ \)とすると，
\[
\begin{eqnarray}
E_{\mathrm {d}} &=&\frac {1}{\pi } \int ^{\pi}_{\alpha }v\sin \omega t \mathrm {d} \left( \omega t \right) \\[ 5pt ] &=&\frac {v}{\pi } \left[ -\cos \omega t \right] ^{\pi}_{\alpha } \\[ 5pt ] &=& \frac {v}{\pi }\left( 1+\cos \alpha \right)
\end{eqnarray}
\] となる。また，\( \ v_{\mathrm {S}} \ \)の実効値\( \ \displaystyle V=\frac {v}{\sqrt {2}} \ \)であるから，
\[
\begin{eqnarray}
E_{\mathrm {d}} &=&\frac {\sqrt{2} V}{\pi }\left( 1+\cos \alpha \right) \\[ 5pt ] &≒&0.45 V\left( 1+\cos \alpha \right) \\[ 5pt ] &=& 0.9 V\frac {1+\cos \alpha }{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。

※　本問は積分を使用するため，積分を使用しない場合は暗記することになります。解法としては電験三種の範囲外と思われます。