《機械》〈直流機〉[R06上:問2]直流電動機の入力電圧を変化させたときの回転速度の変化に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

電機子回路の抵抗が\( \ 0.20 \ \mathrm {\Omega } \ \)の直流他励電動機がある。励磁電流，電機子電流とも一定になるように制御されており，電機子電流は\( \ 50 \ \mathrm {A} \ \)である。回転速度が\( \ 1 \ 200 \ \mathrm {min^{-1}} \ \)のとき，電機子回路への入力電圧は\( \ 110 \ \mathrm {V} \ \)であった。励磁電流，電機子電流を一定に保ったまま電動機の負荷を変化させたところ，入力電圧が\( \ 80 \ \mathrm {V} \ \)となった。このときの回転速度\( \ \mathrm {[min^{-1}]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，電機子反作用はなく，ブラシの抵抗は無視できるものとする。

　(1)　\( \ 764 \ \)　　(2)　\( \ 840 \ \)　　(3)　\( \ 873 \ \)　　(4)　\( \ 900 \ \)　　(5)　\( \ 960 \ \)

【ワンポイント解説】

直流電動機の入力電圧を変化させたときの回転速度の変化を導出する問題です。
直流電動機の等価回路や誘導起電力の関係式は，電験合格のためには必須の知識となります。直流電動機の計算問題は毎年のように出題されますので，ぜひ解けるようにしておいて下さい。
本問は平成21年問2からの再出題となります。

1.直流他励電動機の等価回路と特性
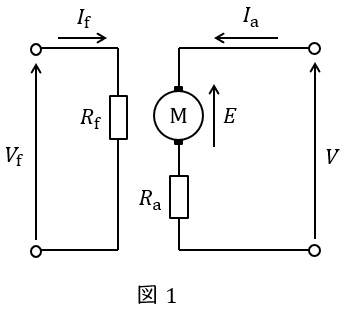
直流他励電動機の等価回路を図1に示します。ただし，図において，\( \ E \ \mathrm {[V]} \ \)は誘導起電力（逆起電力），\( \ V \ \mathrm {[V]} \ \)は端子電圧，\( \ I_{\mathrm {a}} \ \mathrm {[A]} \ \)は電機子電流，\( \ I_{\mathrm {f}} \ \mathrm {[A]} \ \)は界磁電流，\( \ R_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)は電機子抵抗，\( \ R_{\mathrm {f}} \ \mathrm {[\Omega ]} \ \)は界磁抵抗です。
等価回路より，回路方程式は，
\[
\begin{eqnarray}
V &=&E+R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] となります。
また，磁束を\( \ \phi \ \mathrm {[Wb]} \ \)，回転速度を\( \ N \ \mathrm {[{min}^{-1}]} \ \)とすると，\( \ \phi ∝ I_{\mathrm {f}} \ \)となるので，誘導起電力(逆起電力)\( \ E \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
E &=&k_{\mathrm {e}}\phi N \\[ 5pt ] &=&k_{\mathrm {e}}^{\prime } I_{\mathrm {f}} N \\[ 5pt ] \end{eqnarray}
\] となり，トルク\( \ T \ \mathrm {[N\cdot m]} \ \)は，
\[
\begin{eqnarray}
T &=&k_{\mathrm {f}}\phi I_{\mathrm {a}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

解答：(2)
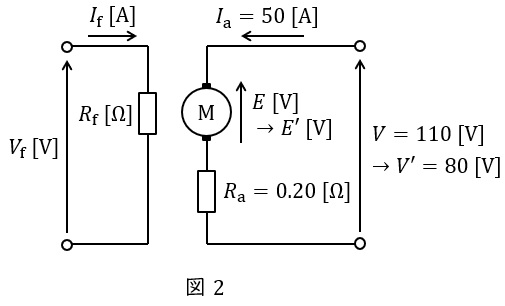
題意に沿って負荷変化前後の等価回路を描くと図2のようになる。
等価回路より，負荷変化前の逆起電力\( \ E \ \mathrm {[V]} \ \)及び負荷変化後の逆起電力\( \ E^{\prime } \ \mathrm {[V]} \ \)は，ワンポイント解説「1.直流他励電動機の等価回路と特性」の通り，
\[
\begin{eqnarray}
E &=&V-R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] &=&110-0.20\times 50 \\[ 5pt ] &=&100 \ \mathrm {[V]} \\[ 5pt ] E^{\prime } &=&V^{\prime }-R_{\mathrm {a}}I_{\mathrm {a}} \\[ 5pt ] &=&80-0.20\times 50 \\[ 5pt ] &=&70 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となり，ワンポイント解説「1.直流他励電動機の等価回路と特性」の通り，逆起電力は回転速度に比例するので，負荷変化前の回転速度を\( \ N=1 \ 200 \ \mathrm {[min^{-1}]} \ \)，負荷変化後の回転速度を\( \ N^{\prime } \ \mathrm {[min^{-1}]} \ \)とすれば，
\[
\begin{eqnarray}
N^{\prime } &=&\frac {E^{\prime }}{E}N \\[ 5pt ] &=&\frac {70}{100}\times 1 \ 200 \\[ 5pt ] &=&840 \ \mathrm {[min^{-1}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。