Contents
【問題】
【難易度】★★★☆☆(普通)
定格容量\( \ 100 \ \mathrm {kV\cdot A} \ \),定格一次電圧\( \ 6.3 \ \mathrm {kV} \ \)で特性の等しい単相変圧器が\( \ 2 \ \)台あり,各変圧器の定格負荷時の負荷損は\( \ 1 \ 600 \ \mathrm {W} \ \)である。この変圧器\( \ 2 \ \)台を\( \ \mathrm {V-V} \ \)結線し,一次電圧\( \ 6.3 \ \mathrm {kV} \ \)にて\( \ 90 \ \mathrm {kW} \ \)の三相平衡負荷をかけたとき,\( \ 2 \ \)台の変圧器の負荷損の合計値\( \ \mathrm {[W]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,負荷の力率は\( \ 1 \ \)とする。
(1) \( \ 324 \ \) (2) \( \ 432 \ \) (3) \( \ 648 \ \) (4) \( \ 864 \ \) (5) \( \ 1 \ 440 \ \)
【ワンポイント解説】
\( \ \mathrm {V-V} \ \)結線をした変圧器の負荷損を求める問題です。
\( \ \mathrm {V-V} \ \)結線の利用率は導出できるとなお良いですが,一先ず問題を解くためには覚えておくことも必要です。電力科目でも活用する知識なので,覚えておくようにして下さい。
本問は平成16年問8からの再出題となります。
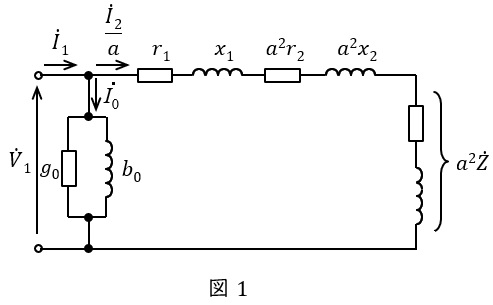
1.変圧器の等価回路(一次換算)と鉄損及び銅損
変圧器の一次側換算簡易等価回路を図1に示します。ただし,\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流,\( \ {\dot I}_{2} \ \mathrm {[A]} \ \)は二次電流,\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流,\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗,\( \ r_{2} \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗,\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス,\( \ x_{2} \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンス,\( \ g_{0} \ \mathrm {[S]} \ \)は励磁コンダクタンス,\( \ b_{0} \ \mathrm {[S]} \ \)は励磁サセプタンス,\( \ a \ \)は変圧比(巻数比)となります。
等価回路より,鉄損(\( \ g_{0} \ \mathrm {[S]} \ \)での損失)は電圧\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)の\( \ 2 \ \)乗に比例し,銅損(\( \ r_{1} \ \mathrm {[\Omega ]} \ \),\( \ r_{2} \ \mathrm {[\Omega ]} \ \)での損失の合計)は電流\( \ {\dot I}_{2} \ \mathrm {[A]} \ \)の\( \ 2 \ \)乗に比例することがわかります。
2.\( \ \mathrm {\Delta -\Delta } \ \)結線と\( \ \mathrm {V-V} \ \)結線の比較
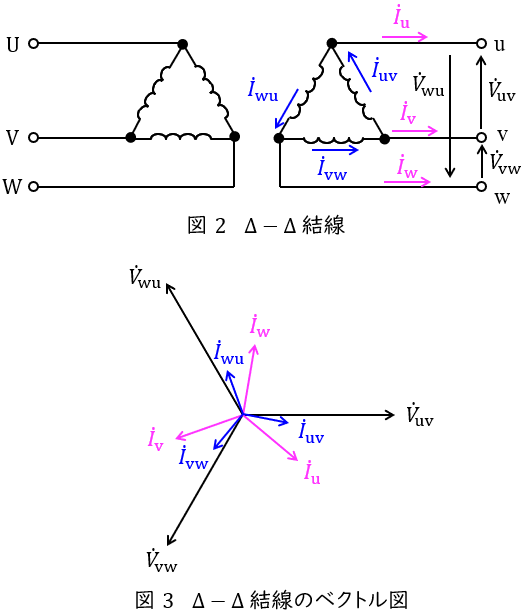
①\( \ \mathrm {\Delta -\Delta } \ \)結線
\( \ \mathrm {\Delta -\Delta } \ \)結線の変圧器の回路図とベクトル図を図2及び図3に示します。
図2において,負荷電流\( \ {\dot I}_{\mathrm {u}} \ \mathrm {[A]} \ \)は,変圧器を流れる電流\( \ {\dot I}_{\mathrm {uv}} \ \mathrm {[A]} \ \)及び\( \ {\dot I}_{\mathrm {wu}} \ \mathrm {[A]} \ \)を用いて,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {u}}&=& {\dot I}_{\mathrm {uv}}-{\dot I}_{\mathrm {wu}} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,ベクトル図上では図3のような関係となり,三相平衡である場合にはそれぞれの大きさの比は,
\[
\begin{eqnarray}
I_{\mathrm {u}}&=& \sqrt {3}I_{\mathrm {uv}} \\[ 5pt ]
\end{eqnarray}
\]
であることが分かります。したがって,各変圧器が分担する容量\( \ S \ \mathrm {[V\cdot A]} \ \)は,負荷の線間電圧を\( \ V_{\mathrm {uv}}=V_{\mathrm {vw}}=V_{\mathrm {wu}}=V \ \),負荷電流を\( \ I_{\mathrm {u}}=I_{\mathrm {v}}=I_{\mathrm {w}}=I \ \)とすると,
\[
\begin{eqnarray}
S&=& \frac {VI}{\sqrt {3}} \\[ 5pt ]
\end{eqnarray}
\]
となります。したがって,変圧器全体の送電電力\( \ P \ \mathrm {[W]} \ \)は力率を\( \ \cos \theta \ \)とすると,
\[
\begin{eqnarray}
P&=& 3S\cos \theta \\[ 5pt ]
&=& 3\cdot \frac {VI}{\sqrt {3}}\cdot \cos \theta \\[ 5pt ]
&=&\sqrt {3}VI \cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となります。
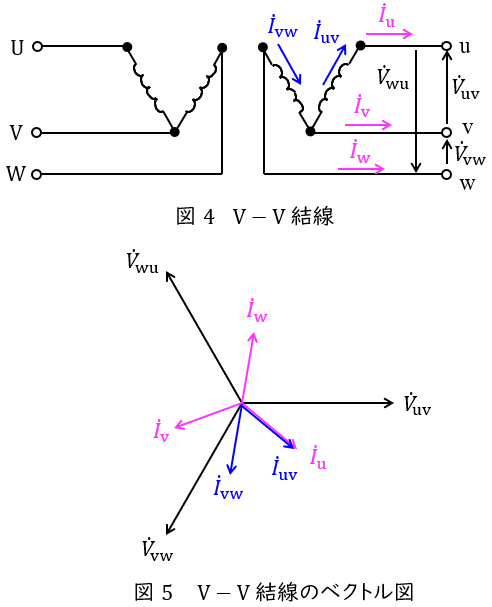
②\( \ \mathrm {V -V } \ \)結線
\( \ \mathrm {V -V } \ \)結線の変圧器の回路図とベクトル図を図4及び図5に示します。
図4において,負荷電流\( \ {\dot I}_{\mathrm {u}} \ \mathrm {[A]} \ \),\( \ {\dot I}_{\mathrm {v}} \ \mathrm {[A]} \ \),\( \ {\dot I}_{\mathrm {w}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {u}}&=& {\dot I}_{\mathrm {uv}} \\[ 5pt ]
{\dot I}_{\mathrm {v}}&=& {\dot I}_{\mathrm {vw}}-{\dot I}_{\mathrm {uv}} \\[ 5pt ]
{\dot I}_{\mathrm {w}}&=& -{\dot I}_{\mathrm {vw}} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,ベクトル図上では図5のような関係となり,三相平衡である場合にはそれぞれの大きさの比は,
\[
\begin{eqnarray}
I_{\mathrm {u}}&=&I_{\mathrm {v}}&=&I_{\mathrm {w}}&=&I_{\mathrm {uv}}&=&I_{\mathrm {vw}} \\[ 5pt ]
\end{eqnarray}
\]
であることが分かります。したがって,各変圧器が分担する容量\( \ S \ \mathrm {[V\cdot A]} \ \)は,負荷の線間電圧を\( \ V_{\mathrm {uv}}=V_{\mathrm {vw}}=V_{\mathrm {wu}}=V \ \),負荷電流を\( \ I_{\mathrm {u}}=I_{\mathrm {v}}=I_{\mathrm {w}}=I \ \)とすると,
\[
\begin{eqnarray}
S&=& VI \\[ 5pt ]
\end{eqnarray}
\]
となります。変圧器全体の送電電力\( \ P_{\mathrm {V}} \ \mathrm {[W]} \ \)は力率を\( \ \cos \theta \ \)とすると,
\[
\begin{eqnarray}
P_{\mathrm {V}}&=& \sqrt {3}VI \cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \mathrm {V -V } \ \)結線で得られる出力\( \ \mathrm {[V\cdot A]} \ \)は各変圧器の出力の\( \ \sqrt {3} \ \)倍となるため,利用率は,
\[
\begin{eqnarray}
利用率&=& \frac {\sqrt {3}VI}{2VI} \\[ 5pt ]
&=& \frac {\sqrt {3}}{2} → 86.6 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,\( \ \mathrm {V -V } \ \)結線と\( \ \mathrm {\Delta -\Delta } \ \)結線で同じ電力を出力する場合に必要となる変圧器の容量比は,
\[
\begin{eqnarray}
容量比&=& \frac {\displaystyle \frac {VI}{\sqrt {3}}}{VI} \\[ 5pt ]
&=& \frac {1}{\sqrt {3}} → 57.7 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となるため,\( \ \mathrm {V -V } \ \)結線の出力は\( \ \mathrm {\Delta -\Delta } \ \)結線の\( \ 57.7 \ \mathrm {[%]} \ \)程度であることがわかります。
【解答】
解答:(4)
\( \ P=90 \ \mathrm {[kW]} \ \)で力率\( \ 1 \ \)の負荷に電力を供給するために各変圧器が分担する容量を\( \ P_{1} \ \mathrm {[kV\cdot A]} \ \)とすると,ワンポイント解説「2.\( \ \mathrm {\Delta -\Delta } \ \)結線と\( \ \mathrm {V-V} \ \)結線の比較」の通り,
\[
\begin{eqnarray}
\frac {P}{2P_{1}}&=& \frac {\sqrt {3}}{2} \\[ 5pt ]
\end{eqnarray}
\]
の関係があるため,これを整理すると,
\[
\begin{eqnarray}
\frac {90}{P_{1}}&=& \sqrt {3} \\[ 5pt ]
P_{1}&=& \frac {90}{\sqrt {3}} \\[ 5pt ]
&≒&51.96 \ \mathrm {[kV\cdot A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。負荷損は出力の\( \ 2 \ \)乗に比例するので,各変圧器の負荷損\( \ P_{\mathrm {c}} \ \mathrm {[W]} \ \)は,ワンポイント解説「1.変圧器の等価回路(一次換算)と鉄損及び銅損」の通り,
\[
\begin{eqnarray}
P_{\mathrm {c}}&=&\left( \frac {51.96}{100}\right) ^{2}\times 1 \ 600 \\[ 5pt ]
&≒&432.0 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ 2 \ \)台の負荷損の合計値\( \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
2P_{\mathrm {c}}&=&2\times 432.0 \\[ 5pt ]
&=&864 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは