Contents
【問題】
【難易度】★★★☆☆(普通)
可動コイル形計器について,次の(a)及び(b)に答えよ。
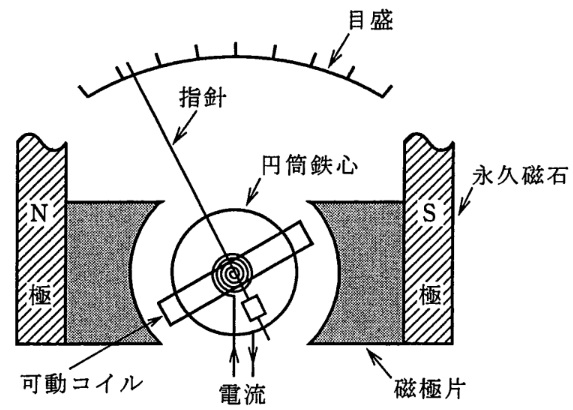
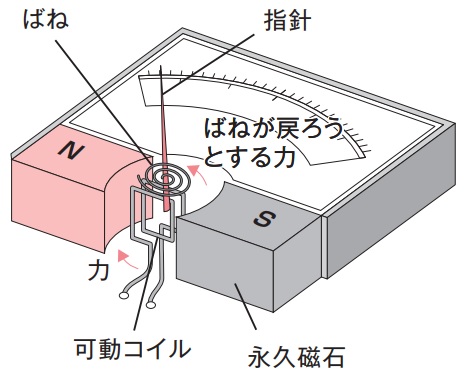
(a) 次の文章は,可動コイル形電流計の原理について述べたもので,図はその構造を示す原理図である。
計器の指針に働く電流によるトルクは,その電流の\( \ \fbox { (ア) } \ \)に比例する。これに脈流を流すと可動部の\( \ \fbox { (イ) } \ \)モーメントが大きいので,指針は電流の\( \ \fbox { (ウ) } \ \)を指示する。
この計器を電圧計として使用する場合,\( \ \fbox { (エ) } \ \)を使う。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる語句として,正しいものを組み合わせたのは次のうちどれか。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & 1 乗 & 慣 性 & 平均値 & 倍率器 \\
\hline
(2) & 1 乗 & 回 転 & 平均値 & 分流器 \\
\hline
(3) & 1 乗 & 回 転 & 瞬時値 & 倍率器 \\
\hline
(4) & 2 乗 & 回 転 & 実効値 & 分流器 \\
\hline
(5) & 2 乗 & 慣 性 & 実効値 & 倍率器 \\
\hline
\end{array}
\]
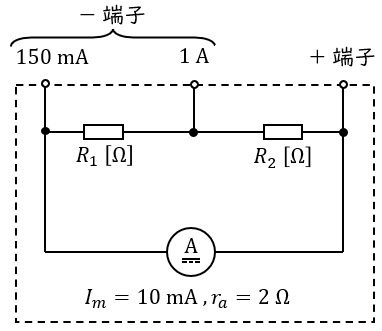
(b) 内部抵抗\( \ r_{a}=2 \ \mathrm {[\Omega ]} \ \),最大目盛\( \ I_{m}=10 \ \mathrm {[mA]} \ \)の可動コイル形電流計を用いて,最大\( \ 150 \ \mathrm {[mA]} \ \)と最大\( \ 1 \ \mathrm {[A]} \ \)の直流電流を測定できる多重範囲の電流計を作りたい。そこで,図のような二つの-端子を有する多重範囲の電流計を考えた。抵抗\( \ R_{1} \ \mathrm {[\Omega ]} \ \),\( \ R_{2} \ \mathrm {[\Omega ]} \ \)の値として,最も近いものを組み合わせたのは次のうちどれか。
\[
\begin{array}{ccc}
& R_{1} \ \mathrm {[\Omega ]} & R_{2} \ \mathrm {[\Omega ]} \\
\hline
(1) & 0.12 & 0.021 \\
\hline
(2) & 0.12 & 0.042 \\
\hline
(3) & 0.14 & 0.021 \\
\hline
(4) & 0.24 & 0.012 \\
\hline
(5) & 0.24 & 0.042 \\
\hline
\end{array}
\]
【ワンポイント解説】
可動コイル形計器に関する知識を問う問題と測定範囲の拡大に関する問題を組み合わせた問題です。
(b)の問題が少し細かい数値になり不安になってしまいそうですが,落ち着いて丁寧に解いていけば正答に辿り着くかと思います。試験本番でも慌てないように注意しましょう。
1.可動コイル形計器
直流電流によりコイルに加わる電磁力により,針を動かして電流を測定する計器で,一般的な直流電流計で利用されている原理です。指針に働くトルクは電流の大きさに比例します。直流用であるため,交流で使用すると平均値を測定し,振動してしまう可能性があります。
出典:みんなが欲しかった!電験三種 理論の実践問題集P.174 (TAC出版)
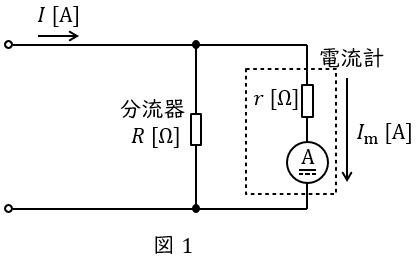
2.分流器
電流計に並列につなぐ抵抗器のことで,電流計の測定できる範囲を拡大することができるものです。図1のように電圧計の内部抵抗を\( \ r \ \mathrm {[\Omega ]} \ \),分流器の抵抗を\( \ R \ \mathrm {[\Omega ]} \ \)とすると,電流計に流れる電流\( \ I_{\mathrm {m}} \ \mathrm {[A]} \ \)は,分流の法則より,
\[
\begin{eqnarray}
I_{\mathrm {m}} &=&\frac {R}{R+r}I \\[ 5pt ]
\end{eqnarray}
\]
となり,倍率\( \ \displaystyle m=\frac {I}{I_{\mathrm {m}}} \ \)は,
\[
\begin{eqnarray}
m&=&\frac {I}{I_{\mathrm {m}}} \\[ 5pt ]
&=&\frac {R+r}{R} \\[ 5pt ]
&=&1+\frac {r}{R} \\[ 5pt ]
\end{eqnarray}
\]
となります。よって,分流器の抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の大きさは,
\[
\begin{eqnarray}
m&=&1+\frac {r}{R} \\[ 5pt ]
\frac {r}{R}&=&m-1 \\[ 5pt ]
R&=&\frac {r}{m-1} \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
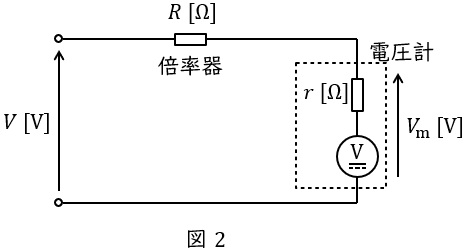
3.倍率器
電圧計に直列につなぐ抵抗器のことで,電圧計の測定できる範囲を拡大することができるものです。図2のように電圧計の内部抵抗を\( \ r \ \mathrm {[\Omega ]} \ \),倍率器の抵抗を\( \ R \ \mathrm {[\Omega ]} \ \)とすると,電圧計に加わる電圧\( \ V_{\mathrm {m}} \ \mathrm {[V]} \ \)は,分圧の法則より,
\[
\begin{eqnarray}
V_{\mathrm {m}} &=&\frac {r}{R+r}V \\[ 5pt ]
\end{eqnarray}
\]
となり,倍率\( \ \displaystyle m=\frac {V}{V_{\mathrm {m}}} \ \)は,
\[
\begin{eqnarray}
m&=&\frac {V}{V_{\mathrm {m}}} \\[ 5pt ]
&=&\frac {R+r}{r} \\[ 5pt ]
&=&1+\frac {R}{r} \\[ 5pt ]
\end{eqnarray}
\]
となります。よって,倍率器の抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の大きさは,
\[
\begin{eqnarray}
m&=&1+\frac {R}{r} \\[ 5pt ]
\frac {R}{r}&=&m-1 \\[ 5pt ]
R&=&\left( m-1\right) r\\[ 5pt ]
\end{eqnarray}
\]
と求められます。
【解答】
(a)解答:(1)
(ア)
ワンポイント解説「1.可動コイル形計器」の通り,計器の指針に働く電流によるトルクは,電流の\( \ 1 \ \)乗に比例します。
(イ)
可動コイル形計器に脈流を流した場合,可動部の慣性モーメント(≒回転のしにくさ)が大きい場合には,指針は大きく触れずにほぼ一定の値を指示します。
(ウ)
ワンポイント解説「1.可動コイル形計器」の通り,可動コイル形計器の指針は電流の平均値を指示します。
(エ)
ワンポイント解説「3.倍率器」の通り,可動コイル形計器を電圧計として使用する場合は,測定範囲を拡大するため倍率器を使用します。
(b)解答:(1)
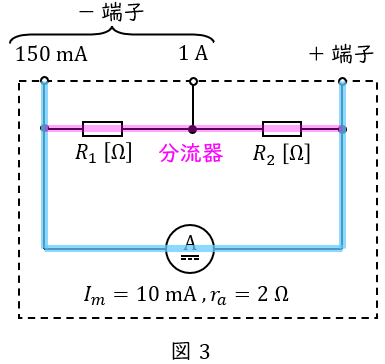
最大\( \ 150 \ \mathrm {[mA]} \ \)を測定する場合,図3に示すように分流器は\( \ \left( R_{1}+R_{2}\right) \ \mathrm {[\Omega ]} \ \)の部分となるため,分流の法則より,
\[
\begin{eqnarray}
I_{\mathrm {m}} &=&\frac {R_{1}+R_{2}}{\left( R_{1}+R_{2}\right) +r_{a}}\cdot 150 \\[ 5pt ]
10 &=&\frac {R_{1}+R_{2}}{R_{1}+R_{2}+2}\cdot 150 \\[ 5pt ]
1 &=&\frac {R_{1}+R_{2}}{R_{1}+R_{2}+2}\cdot 15 \\[ 5pt ]
R_{1}+R_{2}+2 &=&15R_{1}+15R_{2} \\[ 5pt ]
14R_{1}+14R_{2}&=&2 \\[ 5pt ]
7R_{1}+7R_{2}&=&1 ・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となる。
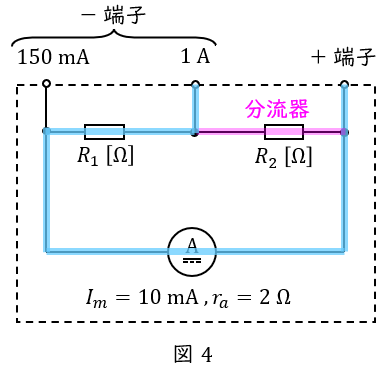
同様に,最大\( \ 1 \ \mathrm {[A]} \ \)を測定する場合,図4に示すように分流器は\( \ R_{2} \ \mathrm {[\Omega ]} \ \)の部分となるため,分流の法則より,
\[
\begin{eqnarray}
I_{\mathrm {m}} &=&\frac {R_{2}}{R_{2}+R_{1}+r_{a}}\cdot 1 \ 000 \\[ 5pt ]
10 &=&\frac {R_{2}}{R_{1}+R_{2}+2}\cdot 1 \ 000 \\[ 5pt ]
1 &=&\frac {R_{2}}{R_{1}+R_{2}+2}\cdot 100 \\[ 5pt ]
R_{1}+R_{2}+2 &=&100R_{2} \\[ 5pt ]
R_{1}&=&99R_{2}-2 ・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
となる。
①に②を代入すると,
\[
\begin{eqnarray}
7\left( 99R_{2}-2\right) +7R_{2}&=&1 \\[ 5pt ]
693R_{2}-14 +7R_{2}&=&1 \\[ 5pt ]
700R_{2}&=&15 \\[ 5pt ]
R_{2}&≒&0.0214 \ 3 → 0.021 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められ,これを②に代入すると,
\[
\begin{eqnarray}
R_{1}&=&99\times 0.0214 \ 3 -2 \\[ 5pt ]
&≒&0.12 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは