《理論》〈電磁気〉[R2:問17]平行平板コンデンサの電界の強さ及び絶縁破壊電圧に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

図のように，誘電体の種類，比誘電率，絶縁破壊電界，厚さがそれぞれ異なる三つの平行板コンデンサ①～③がある。極板の形状と大きさは同一で，コンデンサの端効果，初期電荷及び漏れ電流は無視できるものとする。上側の極板に電圧\( \ V_{0} \ \mathrm {[V]} \ \)の直流電源を接続し，下側の極板を接地した。次の(a)及び(b)の問に答えよ。

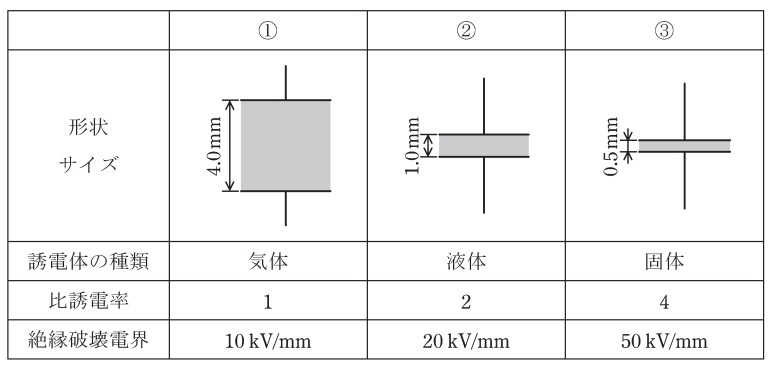
(a)　各平行板コンデンサへの印加電圧の大きさが同一のとき，極板間の電界の強さの大きい順として，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{cc}
\hline
(1) & 　①＞②＞③　 \\
\hline
(2) & 　①＞③＞②　 \\
\hline
(3) & 　②＞①＞③　 \\
\hline
(4) & 　③＞①＞②　 \\
\hline
(5) & 　③＞②＞①　 \\
\hline
\end{array}
\]

(b)　各平行板コンデンサへの印加電圧をそれぞれ徐々に上昇し，極板間の電界の強さが絶縁破壊電界に達したときの印加電圧（絶縁破壊電圧）の大きさの大きい順として，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{cc}
\hline
(1) & 　①＞②＞③　 \\
\hline
(2) & 　①＞③＞②　 \\
\hline
(3) & 　②＞①＞③　 \\
\hline
(4) & 　③＞①＞②　 \\
\hline
(5) & 　③＞②＞①　 \\
\hline
\end{array}
\]

【ワンポイント解説】

平行平板コンデンサの基本公式を理解しているか問う問題です。比較的取り組みやすい問題なので，多くの受験生が正答したものと思われます。合格のためには確実に得点しておきたい問題です。

1.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係
極板間の距離\( \ d \ \)の平行平板コンデンサに電圧\( \ V \ \)をかけると，極板間の電界\( \ E \ \)は，
\[
\begin{eqnarray}
E&=&\frac {V}{d} \\[ 5pt ] \end{eqnarray}
\] となります。

【関連する「電気の神髄」記事】

　　平行平板コンデンサの静電容量まとめ

【解答】

(a)解答：(5)
ワンポイント解説「1.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係」より，印加電圧の大きさ\( \ V \ \)が等しいとき，電界\( \ E \ \)は極板間の距離\( \ d \ \)に反比例する。
したがって，極板間の距離が小さいほど電界が強くなるので，電界の強さの大きい順は\( \ ③＞②＞① \ \)となる。

(b)解答：(2)
ワンポイント解説「1.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係」より絶縁破壊電界がかかったときの\( \ ① \ \)，\( \ ② \ \)，\( \ ③ \ \)のコンデンサの電圧\( \ V_{1} \ \)，\( \ V_{2} \ \)，\( \ V_{3} \ \)は，
\[
\begin{eqnarray}
V_{1}&=&E_{1}d_{1} \\[ 5pt ] &=&10 \times 4.0 \\[ 5pt ] &=&40 \ \mathrm {[kV]} \\[ 5pt ] V_{2}&=&E_{2}d_{2} \\[ 5pt ] &=&20 \times 1.0 \\[ 5pt ] &=&20 \ \mathrm {[kV]} \\[ 5pt ] V_{3}&=&E_{3}d_{3} \\[ 5pt ] &=&50 \times 0.5 \\[ 5pt ] &=&25 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] となるので，極板間の電界の強さが絶縁破壊電界に達したときの印加電圧（絶縁破壊電圧）の大きさの大きい順は，\( \ ①＞③＞② \ \)と求められる。