《理論》〈電磁気〉[H19:問3]電気力線の特徴からの未知の電荷の導出に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

図1に示すように，誘電率\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)の真空中に置かれた静止した二つの電荷\( \ \mathrm {A} \ \mathrm {[C]} \ \)及び\( \ \mathrm {B} \ \mathrm {[C]} \ \)があり，図中にその周囲の電気力線が描かれている。電荷\( \ \mathrm {A}=16\varepsilon _{0} \ \mathrm {[C]} \ \)であるとき，電荷\( \ \mathrm {B} \ \mathrm {[C]} \ \)の値として，正しいのは次のうちどれか。

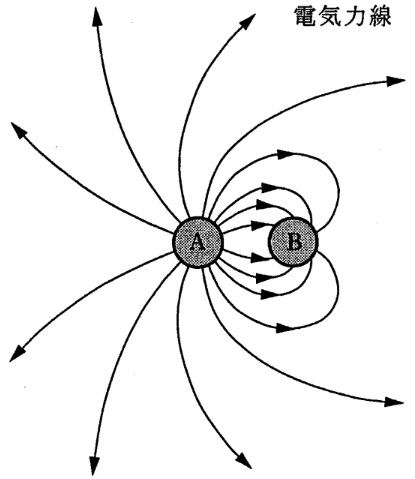
　(1)　\( \ 16\varepsilon _{0} \ \mathrm {[C]} \ \)　　(2)　\( \ 8\varepsilon _{0} \ \mathrm {[C]} \ \)　　(3)　\( \ -4\varepsilon _{0} \ \mathrm {[C]} \ \)　
　(4)　\( \ -8\varepsilon _{0} \ \mathrm {[C]} \ \)　　(5)　\( \ -16\varepsilon _{0} \ \mathrm {[C]} \ \)　　

【ワンポイント解説】

電気力線の特徴に関する問題です。
本問のポイントは電気力線の本数と出ているか入っているかです。そこに注目して解くようにして下さい。

1.電気力線の特徴
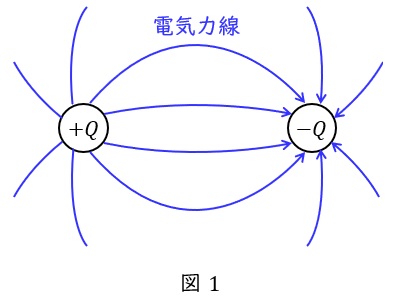
電気力線は正電荷から負電荷に向かう仮想の線で，以下のような特徴があります。言葉ではなく図で覚えておいて，内容を理解した方が良いと思います。
①電気力線の本数は電荷\( \ Q \ \mathrm {[C]} \ \)，誘電率\( \ \varepsilon \ \mathrm {[F/m]} \ \)を用いると，\( \ \displaystyle \frac {Q}{\varepsilon } \ \)本である。
②電気力線は正電荷から垂直に出て，負電荷に垂直に入る。
③電気力線同士は反発し合う。
④電気力線は枝分かれしたり，交差したりしない。
⑤電気力線の向きは電界の向きと一致し，電気力線の密度は電界の大きさに比例する。

【解答】

解答：(4)
問題図より電気力線は導体球\( \ \mathrm {A} \ \)から出ており，導体球\( \ \mathrm {B} \ \)に一部が入っているため，ワンポイント解説「1.電気力線の特徴」の通り，\( \ \mathrm {B} ＜0 \ \)となる。

また，ワンポイント解説「1.電気力線の特徴」の通り，電気力線の本数は導体球の電気量に比例する。よって，電気量\( \ \mathrm {A}=16\varepsilon _{0} \ \mathrm {[C]} \ \)の導体球\( \ \mathrm {A} \ \)から出ている電気力線の本数が\( \ 16 \ \)本であり，導体球\( \ \mathrm {B} \ \)に入る電気力線の本数が\( \ 8 \ \)本であるため，導体球\( \ \mathrm {B} \ \)の電気量は導体球\( \ \mathrm {A} \ \)の半分となる。

以上から，\( \ \mathrm {B}=-8\varepsilon _{0} \ \mathrm {[C]} \ \)と求められる。