《理論》〈電磁気〉[R01:問15]静電界における電気力線及び仕事量に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図のように，平らで十分大きい導体でできた床から高さ\( \ h \ \mathrm {[m]} \ \)の位置に正の電気量\( \ Q \ \mathrm {[C]} \ \)をもつ点電荷がある。次の(a)及び(b)の問に答えよ。ただし，点電荷から床に下ろした垂線の足を点\( \ \mathrm {O} \ \)，床より上側の空間は真空とし，床の導体は接地されている。真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F／m]} \ \)とする。

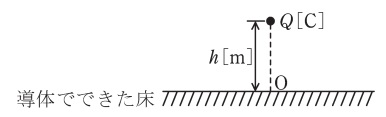
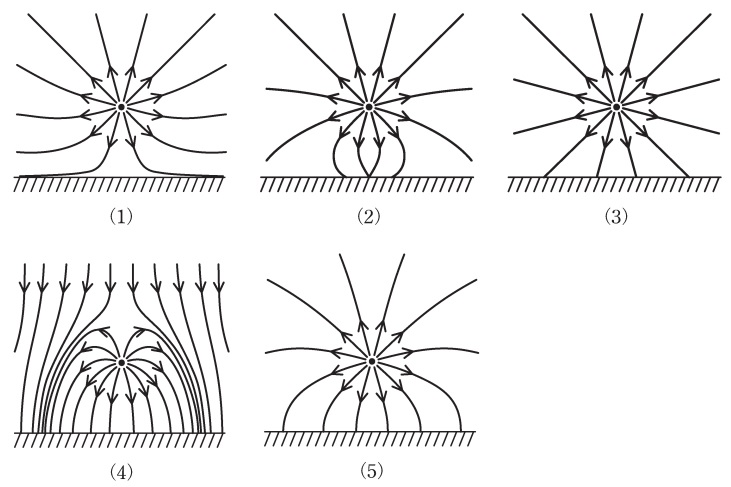
(a)　床より上側の電界は，点電荷のつくる電界と，床の表面に静電誘導によって現れた面電荷のつくる電界との和になる。床より上側の電気力線の様子として，適切なものを次の(1)～(5)のうちから一つ選べ。

(b)　点電荷は床表面に現れた面電荷から鉛直方向の静電吸引力\( \ F \ \mathrm {[N]} \ \)を受ける。その力は床のない状態で点\( \ \mathrm {O} \ \)に固定した電気量\( \ \displaystyle -\frac {Q}{4} \ \mathrm {[C]} \ \)の点電荷から受ける静電力に等しい。\( \ F \ \mathrm {[N]} \ \)に逆らって，点電荷を高さ\( \ h \ \mathrm {[m]} \ \)から\( \ z \ \mathrm {[m]} \ \)(ただし\( \ h＜z \ \))まで鉛直方向に引き上げるのに必要な仕事\( \ W \ \mathrm {[J]} \ \)を表す式として，正しいものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ \displaystyle \frac {Q^{2}}{4\pi \varepsilon _{0}z^{2}} \ \)　　(2)　\( \ \displaystyle \frac {Q^{2}}{4\pi \varepsilon _{0}}\left( \frac {1}{h}-\frac {1}{z}\right) \ \) 　　(3)　\( \ \displaystyle \frac {Q^{2}}{16\pi \varepsilon _{0}}\left( \frac {1}{h}-\frac {1}{z}\right) \ \)
　(4)　\( \ \displaystyle \frac {Q^{2}}{16\pi \varepsilon _{0}z^{2}} \ \)　　(5)　\( \ \displaystyle \frac {Q^{2}}{\pi \varepsilon _{0}}\left( \frac {1}{h^{2}}-\frac {1}{z^{2}}\right) \ \)

【ワンポイント解説】

電気力線のポイントは正電荷から出ること，交わらないこと，導体には垂直に出入りすること等があります。電気力線の基本を理解していると，電界や電位の計算もイメージしやすくなるので，確実に理解するようにして下さい。

1.点電荷周辺の電位\( \ V \ \)
真空中に電荷\( \ Q \ \)を置いた時，距離\( \ r \ \)離れた位置の電位\( \ V \ \)は，真空の誘電率を\( \ \varepsilon _{0} \ \)とすると，
\[
\begin{eqnarray}
V &=&\frac {Q}{4\pi \varepsilon _{0}r} \\[ 5pt ] \end{eqnarray}
\] となります。

2.点電荷を移動するのに必要な仕事量\( \ W \ \)
電界に逆らって，真空中に電荷\( \ Q \ \)を\( \ r_{1} \ \)から\( \ r_{2} \ \)に移動した時，その電位差を\( \ \Delta V \ \)とすると，仕事量\( \ W \ \)は，
\[
\begin{eqnarray}
W &=&Q\Delta V \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(5)
電気力線は正電荷から出て，導体には垂直に交わるので，これを満たす図は(4)もしくは(5)となります。
本問において，正電荷以外の電界は与えられていないので，(5)が解答となります。

※「床の表面に静電誘導によって現れた面電荷のつくる電界」という文言が引っ掛けとなっています。(4)のように一様電界は与えられていないので注意するようにして下さい。

(b)解答：(3)
題意より，面電荷から鉛直方向の静電吸引力\( \ F \ \mathrm {[N]} \ \)は床のない状態で点\( \ \mathrm {O} \ \)に固定した電気量\( \ \displaystyle -\frac {Q}{4} \ \mathrm {[C]} \ \)と等しいとなっている。この点電荷の移動に影響を及ぼす電荷は点\( \ \mathrm {O} \ \)に固定した電気量\( \ \displaystyle -\frac {Q}{4} \ \mathrm {[C]} \ \)のみとなるので，仕事量の導出にはこの\( \ \displaystyle -\frac {Q}{4} \ \mathrm {[C]} \ \)による電位の変化のみを考慮すれば良い。電気量\( \ \displaystyle -\frac {Q}{4} \ \mathrm {[C]} \ \)による各電位\( \ V_{\mathrm {h}} \ \)及び\( \ V_{\mathrm {z}} \ \)は，
\[
\begin{eqnarray}
V_{\mathrm {h}} &=&-\frac {Q}{16\pi \varepsilon _{0}h} \\[ 5pt ] V_{\mathrm {z}} &=&-\frac {Q}{16\pi \varepsilon _{0}z} \\[ 5pt ] \end{eqnarray}
\] となるので，その仕事量\( \ W \ \)は，ワンポイント解説「2.点電荷を移動するのに必要な仕事量\( \ W \ \)」より，
\[
\begin{eqnarray}
W &=&Q\Delta V \\[ 5pt ] &=&Q\left( V_{\mathrm {z}}-V_{\mathrm {h}}\right) \\[ 5pt ] &=&Q\left( -\frac {Q}{16\pi \varepsilon _{0}z}+\frac {Q}{16\pi \varepsilon _{0}h}\right) \\[ 5pt ] &=&\frac {Q^{2}}{16\pi \varepsilon _{0}}\left( \frac {1}{h}-\frac {1}{z}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。