《理論》〈電気及び電子計測〉[H20:問16]オシロスコープの原理と考え方に関する空欄穴埋・計算問題

【問題】

【難易度】★★★★☆（やや難しい）

ブラウン管オシロスコープは，水平・垂直偏向電極を有し，波形観測ができる。次の(a)及び(b)に答えよ。

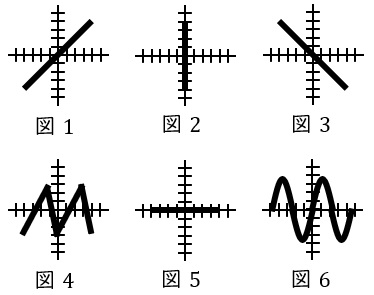
(a)　垂直偏向電極のみに，正弦波交流電圧を加えた場合は，蛍光面に\( \ \fbox {　 （ア） 　} \ \)のような波形が現れる。また，水平偏向電極のみにのこぎり波電圧を加えた場合は，蛍光面に\( \ \fbox {　 （イ） 　} \ \)のような波形が現れる。また，これらの電圧をそれぞれの電極に加えると，蛍光面に\( \ \fbox {　 （ウ） 　} \ \)のような波形が現れる。このとき波形を静止させて見るためには，垂直偏向電極の電圧の周波数と水平偏向電極の電圧の繰返し周波数との比が整数でなければならない。

　上記の記述中の空白箇所(ア)，(イ)及び(ウ)に当てはまる語句として，正しいものを組み合わせたのは次のうちどれか。

\[
\begin{array}{cccc}
& （ア） & （イ） & （ウ） \\
\hline
(1) & 　図　2　 & 　図　4　 & 　図　6　 \\
\hline
(2) & 　図　3　 & 　図　5　 & 　図　1　 \\
\hline
(3) & 　図　2　 & 　図　5　 & 　図　6　 \\
\hline
(4) & 　図　3　 & 　図　4　 & 　図　1　 \\
\hline
(5) & 　図　2　 & 　図　5　 & 　図　1　 \\
\hline
\end{array}
\]

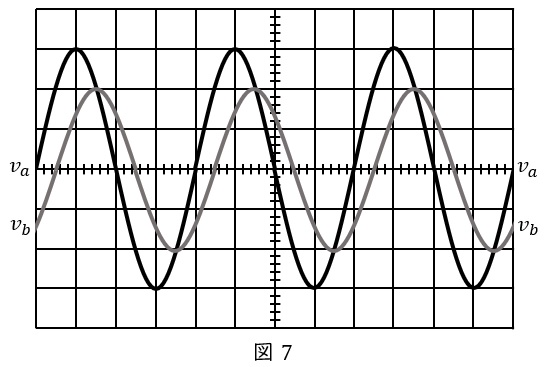
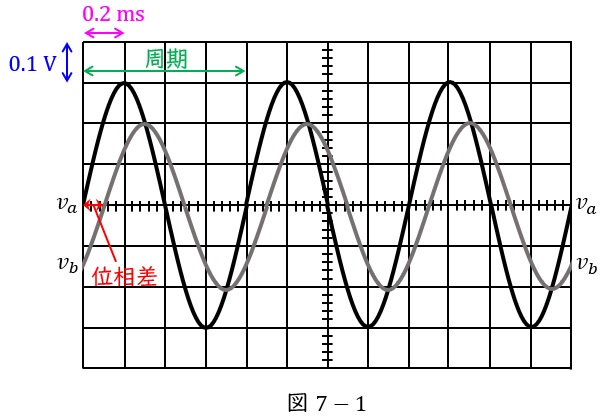
(b)　正弦波電圧\( \ v_{a} \ \)及び\( \ v_{b} \ \)をオシロスコープで観測したところ，蛍光面に図7に示すような電圧波形が現れた。同図から，\( \ v_{a} \ \)の実効値は\( \ \fbox {　 （ア） 　} \ \mathrm {[V]} \ \)，\( \ v_{b} \ \)の周波数は\( \ \fbox {　 （イ） 　} \ \mathrm {[kHz]} \ \)，\( \ v_{a} \ \)の周期は\( \ \fbox {　 （ウ） 　} \ \mathrm {[ms]} \ \)，\( \ v_{a} \ \)と\( \ v_{b} \ \)の位相差は\( \ \fbox {　 （エ） 　} \ \mathrm {[rad]} \ \)であることが分かった。

　ただし，オシロスコープの垂直感度は\( \ 0.1 \ \mathrm {[V] / div} \ \)，掃引時間は\( \ 0.2 \ \mathrm {[ms] / div} \ \)とする。

　上記の記述中の空白箇所(ア)，(イ)，(ウ)及び(エ)に当てはまる最も近い値として，正しいものを組み合わせたのは次のうちどれか。

\[
\begin{array}{ccccc}
& （ア） & （イ） & （ウ） & （エ） \\
\hline
(1) & 　0.21　 & 　1.3　 & 　0.8　 & 　\displaystyle \frac {\pi }{4}　 \\
\hline
(2) & 　0.42　 & 　1.3　 & 　0.4　 & 　\displaystyle \frac {\pi }{3}　 \\
\hline
(3) & 　0.42　 & 　2.5　 & 　0.4　 & 　\displaystyle \frac {\pi }{3}　 \\
\hline
(4) & 　0.21　 & 　1.3　 & 　0.4　 & 　\displaystyle \frac {\pi }{4}　 \\
\hline
(5) & 　0.42　 & 　2.5　 & 　0.8　 & 　\displaystyle \frac {\pi }{2}　 \\
\hline
\end{array}
\]

【ワンポイント解説】

オシロスコープの原理と考え方に関する問題です。
知識があれば難解ではありませんが，そもそも掲載されている電験の参考書の方が少ない印象の内容です。
一度理解してしまえば応用がきく内容となりますので，本問で理解するようにして下さい。

1.オシロスコープの原理と概要
図8にオシロスコープのブラウン管の構成を示します。
ブラウン管はヒータや電極等で構成された電子銃，垂直もしくは水平方向へ偏向する偏向電極，電子ビームを衝突させる蛍光面（スクリーン）等から構成されています。

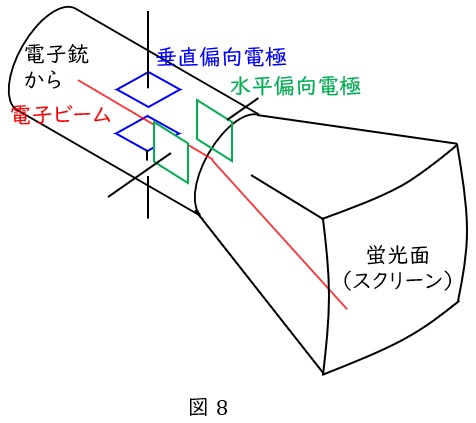
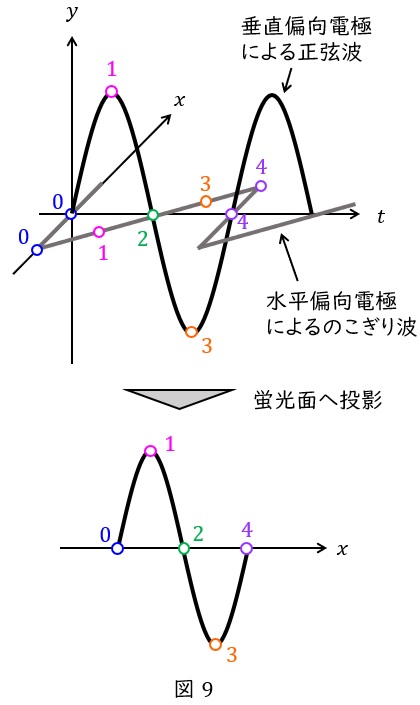
図9に示すように，水平偏向電極にはのこぎり波を加え，時間\( \ t \ \)に対し等速運動していく（掃引）ような出力\( \ x \ \)を出します。
このとき，垂直偏向電極に正弦波を加えその出力\( \ y \ \)を出すと，蛍光面の\( \ xy \ \)平面には図9の下のグラフに示すような正弦波の波形が写し出されます。
図9において，同じ時刻には同じ番号が振られていますので，\( \ x \ \)と\( \ y \ \)の関係を考えてみて下さい。

2.正弦波交流の基本
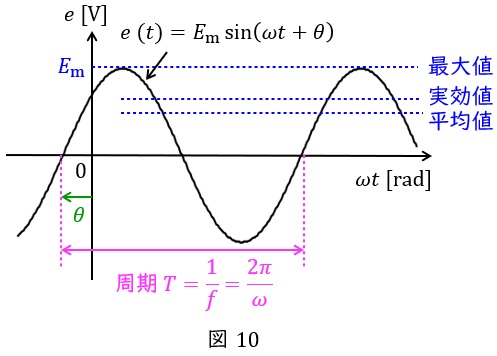
正弦波交流は図10に示されるような波形の交流です。
振幅の大きさ（最大値）を\( \ E_{\mathrm {m}} \ \mathrm {[V]} \ \)，角速度を\( \ \omega \ \mathrm {[rad / s]} \ \)，時間を\( \ t \ \mathrm {[s]} \ \)，初期位相を\( \ \theta \ \mathrm {[rad]} \ \)とすれば，瞬時値\( \ e\left( t \right) \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
e\left( t \right) &=&E_{\mathrm {m}}\sin \left( \omega t +\theta \right) \\[ 5pt ] \end{eqnarray}
\] となり，波形の周期\( \ T \ \mathrm {[s]} \ \)は，周波数を\( \ f \ \mathrm {[Hz]} \ \)とすると，
\[
\begin{eqnarray}
T &=&\frac {1}{f}=\frac {2\pi }{\omega } \\[ 5pt ] \end{eqnarray}
\] の関係があるので，\( \ \omega =2\pi f \ \)となり，
\[
\begin{eqnarray}
e\left( t \right) &=&E_{\mathrm {m}}\sin \left( 2\pi f t +\theta \right) \\[ 5pt ] \end{eqnarray}
\] と表現することもできます。

3.平均値と実効値の定義
\( \ f( \theta ) \ \)を周期\( \ T \ \)の周期関数であるとしたとき，平均値と実効値は以下の通りとなります。
①平均値\( \ F_{\mathrm {av}} \ \)
定義式は，
\[
\begin{eqnarray}
F_{\mathrm {av}}&=&\frac {1}{T}\int _{0}^{T}f( \theta ) \mathrm {d}\theta \\[ 5pt ] \end{eqnarray}
\] であり，これを正弦波\( \ e\left( t \right) =E_{\mathrm {m}}\sin \omega t \ \)に適用すると，
\[
\begin{eqnarray}
E_{\mathrm {av}} &=&\frac {1}{\pi }\int _{0}^{\pi }E_{\mathrm {m}}\sin \omega t \mathrm {d}\omega t \\[ 5pt ] &=&\frac {E_{\mathrm {m}}}{\pi }\left[ -\cos \omega t \right] _{0}^{\pi } \\[ 5pt ] &=&\frac {E_{\mathrm {m}}}{\pi }\left[ 1+1 \right] \\[ 5pt ] &=&\frac {2}{\pi }E_{\mathrm {m}}
\end{eqnarray}
\] となります。

②実効値\( \ F \ \)　
定義式は，
\[
\begin{eqnarray}
F&=&\sqrt {\frac {1}{T} \int _{0}^{T} f( \theta ) ^{2} \mathrm {d}\theta } \\[ 5pt ] \end{eqnarray}
\] であり，これを正弦波\( \ e\left( t \right) =E_{\mathrm {m}}\sin \omega t \ \)に適用すると，
\[
\begin{eqnarray}
E &=&\sqrt {\frac {1}{\pi }\int _{0}^{\pi }{E_{\mathrm {m}}}^{2}\sin ^{2}\omega t \mathrm {d}\omega t} \\[ 5pt ] &=&E_{\mathrm {m}}\sqrt {\frac {1}{\pi }\int _{0}^{\pi }\frac {1-\cos 2\omega t}{2} \mathrm {d}\omega t} \\[ 5pt ] &=&E_{\mathrm {m}}\sqrt {\frac {1}{\pi }\left[ \frac {1}{2}\omega t -\frac {1}{4}\sin 2\omega t \right] _{0}^{\pi } } \\[ 5pt ] &=&E_{\mathrm {m}}\sqrt {\frac {1}{\pi }\left[ \frac {1}{2}\pi -0 -0 +0 \right] _{0}^{\pi } } \\[ 5pt ] &=&\frac {E_{\mathrm {m}}}{\sqrt {2}}
\end{eqnarray}
\] となります。

【解答】

(a)解答：(3)
(ア)
ワンポイント解説「1.オシロスコープの原理と概要」の通り，垂直偏向電極のみに正弦波交流電圧を加えた場合は，横軸は零のまま縦軸の値が上下していくような方な波形となるため，図2のような波形が得られることになります。

(イ)
ワンポイント解説「1.オシロスコープの原理と概要」の通り，水平偏向電極のみにのこぎり波電圧を加えた場合は，縦軸は零のまま横軸が左右に動くような波形となるため，図5のような波形が得られることになります。

(ウ)
ワンポイント解説「1.オシロスコープの原理と概要」の通り，垂直偏向電極及び水平偏向電極にそれぞれの電圧を加えた場合は，図6のような波形が得られることになります。

(b)解答：(1)
(ア)
図7-1に示すように，オシロスコープの垂直感度は\( \ 0.1 \ \mathrm {[V] / div} \ \)なので，\( \ v_{a} \ \)の波高値は\( \ 0.3 \ \mathrm {V} \ \)であり，実効値はワンポイント解説「3.平均値と実効値の定義」の通り，
\[
\begin{eqnarray}
\frac {0.3}{\sqrt {2}}&≒&0.21 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となります。

(イ)
図7-1に示すように，オシロスコープの掃引時間（横軸の\( \ 1 \ \)目盛の時間）は\( \ 0.2 \ \mathrm {[ms] / div} \ \)なので，\( \ v_{b} \ \)の周期\( \ T_{b} \ \)は\( \ 0.8 \ \mathrm {ms} \ \)であり，ワンポイント解説「2.正弦波交流の基本」の通り，周波数\( \ f_{b} \ \)は周期\( \ T_{b} \ \)の逆数なので，
\[
\begin{eqnarray}
f_{b}&=&\frac {1}{T_{b}} \\[ 5pt ] &=&\frac {1}{0.8\times 10^{-3}} \\[ 5pt ] &≒&1.3\times 10^{3} \ \mathrm {[Hz]}　→　1.3 \ \mathrm {[kHz]} \\[ 5pt ] \end{eqnarray}
\] となります。

(ウ)
（イ）と同様に，図7-1に示すように，オシロスコープの掃引時間（横軸の\( \ 1 \ \)目盛の時間）は\( \ 0.2 \ \mathrm {[ms] / div} \ \)なので，\( \ v_{a} \ \)の周期\( \ T_{a} \ \)は\( \ 0.8 \ \mathrm {ms} \ \)となります。

(エ)
図7-1に示すように，\( \ 1 \ \)周期（位相\( \ 2\pi \ \mathrm {[rad]} \ \)）が\( \ 4 \ \)目盛に対し，位相差が\( \ 0.5 \ \)目盛なので，位相差\( \ \theta \ \)は，
\[
\begin{eqnarray}
\theta &=&\frac {0.5}{4}\times 2\pi \\[ 5pt ] &=&\frac {\pi }{4} \ \mathrm {[rad]} \\[ 5pt ] \end{eqnarray}
\] となります。