Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
静電界に関する記述として,正しいのは次のうちどれか。
(1) 二つの小さな帯電体の間に働く力の大きさは,それぞれの帯電体の電気量の和に比例し,その距離の\( \ 2 \ \)乗に反比例する。
(2) 点電荷が作る電界は点電荷の電気量に比例し,距離に反比例する。
(3) 電気力線上の任意の点での接線の方向は,その点の電界の方向に一致する。
(4) 等電位面上の正電荷には,その面に沿った方向に正のクーロン力が働く。
(5) コンデンサの電極板間にすき間なく誘電体を入れると,静電容量と電極板間の電界は,誘電体の誘電率に比例して増大する。
【ワンポイント解説】
静電界における力の大きさや電界の特性を問う問題です。
難解な内容ではありませんが,誤っているものではなく正しいものを選ぶこと,ちょっとした違いに気付く等細かな知識をきちんと理解しているかが問われている問題です。
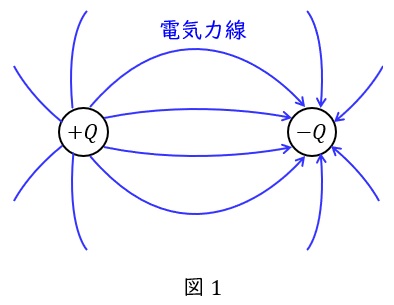
1.電気力線の特徴
電気力線は正電荷から負電荷に向かう仮想の線で,以下のような特徴があります。言葉ではなく図で覚えておいて,内容を理解した方が良いと思います。
①電気力線の本数は電荷\( \ Q \ \mathrm {[C]} \ \),誘電率\( \ \varepsilon \ \mathrm {[F/m]} \ \)を用いると,\( \ \displaystyle \frac {Q}{\varepsilon } \ \)本である。
②電気力線は正電荷から垂直に出て,負電荷に垂直に入る。
③電気力線同士は反発し合う。
④電気力線は枝分かれしたり,交差したりしない。
⑤電気力線の向きは電界の向きと一致し,電気力線の密度は電界の大きさに比例する。
2.クーロンの法則
真空中で距離\( \ r \ \mathrm {[m]} \ \)離れた二つの電荷\( \ Q_{\mathrm {A}} \ \mathrm {[C]} \ \),\( \ Q_{\mathrm {B}} \ \mathrm {[C]} \ \)に加わる力\( \ F \ \mathrm {[N]} \ \)は,真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)とすると,
\[
\begin{eqnarray}
F &=&\frac {Q_{\mathrm {A}}Q_{\mathrm {B}}}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。このとき,\( \ Q_{\mathrm {A}} \ \),\( \ Q_{\mathrm {B}} \ \)の\( \ + \ \)\( \ – \ \)の符号が同符号である場合には斥力(反発する力),異符号である場合には引力(引き合う力)が働きます。
3.真空中の電界の大きさ
真空中に電荷\( \ Q \ \mathrm {[C]} \ \)をおいた時,電荷から距離\( \ r \ \mathrm {[m]} \ \)離れた場所の電界の大きさ\( \ E \ \mathrm {[N / C]} \ \)は,真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)とすると,
\[
\begin{eqnarray}
E &=&\frac {Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。この場所に電荷\( \ q \ \mathrm {[C]} \ \)の電荷を置けば,
\[
\begin{eqnarray}
F &=&qE \\[ 5pt ]
\end{eqnarray}
\]
の力が働きます。
4.平行平板コンデンサの静電容量\( \ C \ \)
平行平板コンデンサの静電容量\( \ C \ \mathrm {[F]} \ \)は,真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \),極板の面積を\( \ S \ \mathrm {[m^{2}]} \ \),極板間の距離を\( \ d \ \mathrm {[m]} \ \)とすると,
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{0}S}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。平行平板コンデンサの間に比誘電率\( \ \varepsilon _{\mathrm {r}} \ \)の誘電体を挿入すると,
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{\mathrm {r}} \varepsilon _{0}S}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。
5.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係
極板間の距離\( \ d \ \mathrm {[m]} \ \)の平行平板コンデンサに電圧\( \ V \ \mathrm {[V]} \ \)をかけると,極板間の電界\( \ E \ \mathrm {[V / m]} \ \)は,
\[
\begin{eqnarray}
E&=&\frac {V}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
解答:(3)
(1)誤り
ワンポイント解説「2.クーロンの法則」の通り,二つの小さな帯電体\( \ Q_{\mathrm {A}} \ \),\( \ Q_{\mathrm {B}} \ \)の間に働く力の大きさは,
\[
\begin{eqnarray}
F &=&\frac {Q_{\mathrm {A}}Q_{\mathrm {B}}}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
で表され,それぞれの帯電体の電気量の積に比例し,その距離\( \ r \ \)の\( \ 2 \ \)乗に反比例します。
(2)誤り
ワンポイント解説「3.真空中の電界の大きさ」の通り,点電荷が作る電界は,
\[
\begin{eqnarray}
E &=&\frac {Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
で表され,点電荷の電気量\( \ Q \ \)に比例し,距離\( \ \underline {r} \ \)の\( \ \underline {2} \ \)乗に反比例します。
(3)正しい
ワンポイント解説「1.電気力線の特徴」の通り,電気力線上の任意の点での接線の方向は,その点の電界の方向となります。
(4)誤り
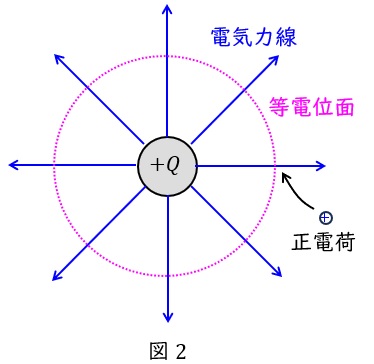
例えば図2のような正電荷が作る電界について,電気力線及び等電位面は図2に示す通りとなり,等電位面上に正電荷を置いた場合には,その面に垂直な方向にクーロン力が働きます。
(5)誤り
ワンポイント解説「4.平行平板コンデンサの静電容量\( \ C \ \)」及び「5.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係」の通り,コンデンサの電極板間にすき間なく誘電体を入れると,静電容量は誘電体の誘電率に比例して増大しますが,電極板間の電界は,誘電体の誘電率に関係しません。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは