《理論》〈電気回路〉[H22:問5]直流回路の抵抗での消費電力からの未知抵抗の導出に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

図の直流回路において，\( \ 12 \ \mathrm {[\Omega ]} \ \)の抵抗の消費電力が\( \ 27 \ \mathrm {[W]} \ \)である。このとき，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の値として，正しいのは次のうちどれか。

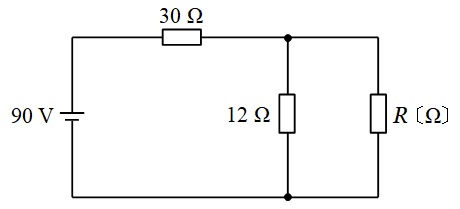
　(1)　\( \ 4.5 \ \)　　(2)　\( \ 7.5 \ \)　　(3)　\( \ 8.6 \ \)　　(4)　\( \ 12 \ \)　　(5)　\( \ 20 \ \)

【ワンポイント解説】

諸条件から未知の抵抗値を求める問題です。
一気に求めるのではなく，一つ一つも求められるものを求めていき，最終的に目的の抵抗値を求めます。
電験合格のためには，是非とも得点しておきたい問題です。

1.キルヒホッフの法則
キルヒホッフの法則には第1法則と第2法則がありますが，法則を説明できる必要はなく，計算で使いこなせることが重要です。
①第1法則（電流則）
　回路の接続点に流入する電流の和と流出する電流の和が等しい。

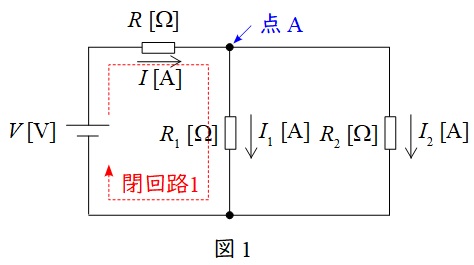
　図1で言えば，例えば接続点\( \ \mathrm {A} \ \)において，
\[
\begin{eqnarray}
I &=&I_{1}+I_{2} \\[ 5pt ] \end{eqnarray}
\] 　となります。

②第2法則（電圧則）
　任意の閉回路において，起電力の総和と抵抗の電圧降下の和は等しい。

　図1で言えば，例えば閉回路\( \ 1 \ \)において，
\[
\begin{eqnarray}
V &=&RI+R_{1}I_{1} \\[ 5pt ] \end{eqnarray}
\] 　となります。

2.抵抗での消費電力
ある抵抗\( \ R \ \mathrm {[\Omega ]} \ \)に電圧\( \ V \ \mathrm {[V]} \ \)をかけたとき抵抗に電流\( \ I \ \mathrm {[A]} \ \)が流れたとすると，\( \ R \ \mathrm {[\Omega ]} \ \)での消費電力\( \ P \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P &=&VI \\[ 5pt ] \end{eqnarray}
\] となります。オームの法則\( \ V=RI \ \)より上式は，
\[
\begin{eqnarray}
P &=&RI^{2} \\[ 5pt ] &=&\frac {V^{2}}{R} \\[ 5pt ] \end{eqnarray}
\] と変形できます。

【解答】

解答：(5)
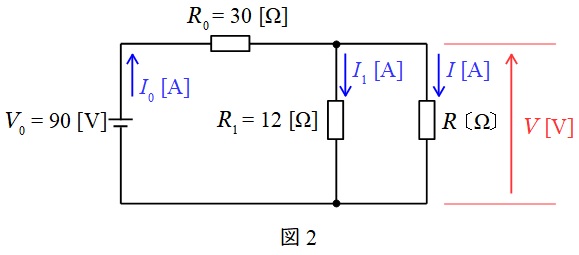
図2のように各電圧，電流及び抵抗をおく。
抵抗\( \ R_{1}=12 \ \mathrm {[\Omega ]} \ \)の消費電力が\( \ P_{1}=27 \ \mathrm {[W]} \ \)であることから，電流\( \ I_{1} \ \mathrm {[A]} \ \)は，ワンポイント解説「2.抵抗での消費電力」の通り，
\[
\begin{eqnarray}
P_{1} &=&R_{1}I_{1}^{2} \\[ 5pt ] I_{1}^{2} &=&\frac {P_{1}}{R_{1}} \\[ 5pt ] I_{1}&=&\sqrt {\frac {P_{1}}{R_{1}}} \\[ 5pt ] &=&\sqrt {\frac {27}{12}} \\[ 5pt ] &=&1.5 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ V \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
P_{1} &=&VI_{1} \\[ 5pt ] V &=&\frac {P_{1}}{I_{1}} \\[ 5pt ] &=&\frac {27}{1.5} \\[ 5pt ] &=&18 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。これより，抵抗\( \ R_{0}=30 \ \mathrm {[\Omega ]} \ \)を流れる電流\( \ I_{0} \ \mathrm {[A]} \ \)は，ワンポイント解説「1.キルヒホッフの法則」の通り，
\[
\begin{eqnarray}
V_{0}-V &=&R_{0}I_{0} \\[ 5pt ] I_{0} &=&\frac {V_{0}-V}{R_{0}} \\[ 5pt ] &=&\frac {90-18}{30} \\[ 5pt ] &=&2.4 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)を流れる電流\( \ I \ \mathrm {[A]} \ \)は，ワンポイント解説「1.キルヒホッフの法則」の通り，
\[
\begin{eqnarray}
I &=&I_{0}-I_{1} \\[ 5pt ] &=&2.4-1.5 \\[ 5pt ] &=&0.9 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。以上から，抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の大きさは，
\[
\begin{eqnarray}
R &=&\frac {V}{R} \\[ 5pt ] &=&\frac {18}{0.9} \\[ 5pt ] &=&20 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。