《理論》〈電子理論〉[H26:問13]演算増幅器を用いた能動回路に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

図のような，演算増幅器を用いた能動回路がある。直流入力電圧\(V_{\mathrm {in}} \ \mathrm {[V]}\)が\(3 \ \mathrm {V}\)のとき，出力電圧\(V_{\mathrm {out}} \ \mathrm {[V]}\)として，最も近い\(V_{\mathrm {out}}\)の値を次の(1)～(5)のうちから一つ選べ。

ただし，演算増幅器は，理想的なものとする。

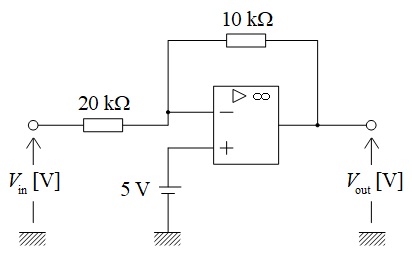
(1)　\(1.5\)　　(2)　\(5\)　　(3)　\(5.5\)　　(4)　\(6\)　　(5)　\(6.5\)

【ワンポイント解説】

演算増幅器の特徴を理解していれば，あとは単純な計算となります。演算増幅器の問題はほぼパターン化されているので，確実に解けるように過去問を習熟しましょう。

1.理想的な演算増幅器の特徴
　１．電圧増幅率が無限大である。したがって，無限大でない有限数が出力される時，入力端子間の電圧は\(0\mathrm {V}\)(バーチャルショート)となる。
　２．入力インピーダンスが無限大である。したがって入力端子に電流は流れない。
　３．出力インピーダンスがゼロである。

【解答】

解答：(4)
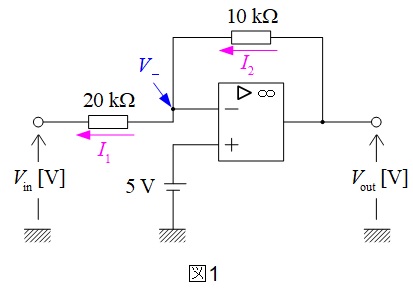
図1のように各部の電圧電流を置く。ワンポイント解説「1.理想的な演算増幅器の特徴」の通り，演算増幅器の入力端子間の電圧は零なので，\(V_{-}=5 \ \mathrm {V}\)となる。したがって，\(20 \ \mathrm {k\Omega }\)を流れる電流は右から左へ流れ，その大きさは，
\[
\begin{eqnarray}
I_{1} &=&\frac {5-3}{20\times 10^{3}} \\[ 5pt ] &=&1.0\times 10^{-4} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「1.理想的な演算増幅器の特徴」より，入力端子には電流は流れないので，
\[
\begin{eqnarray}
I_{2} &=&I_{1} \\[ 5pt ] &=&1.0\times 10^{-4} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，出力電圧\(V_{\mathrm {out}}\)は，
\[
\begin{eqnarray}
V_{\mathrm {out}} &=&V_{-} + 10\times 10^{3} \times I_{2} \\[ 5pt ] &=&5 + 10\times 10^{3} \times 1.0\times 10^{-4} \\[ 5pt ] &=&6 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。