《理論》〈電気回路〉[R2:問8]交流回路に流れる電流からの抵抗値の導出に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

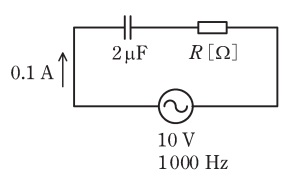
図のように，静電容量\( \ 2 \ \mathrm {\mu F } \ \)のコンデンサ，\( \ R \ \mathrm {[\Omega ]} \ \)の抵抗を直列に接続した。この回路に，正弦波交流電圧\( \ 10 \ \mathrm {V} \ \)，周波数\( \ 1000 \ \mathrm {Hz} \ \)を加えたところ，電流\( \ 0.1 \ \mathrm {A} \ \)が流れた。抵抗\( \ R \ \)の値\( \ \mathrm {[\Omega ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 4.50 \ \)　　(2)　\( \ 20.4 \ \)　　(3)　\( \ 30.3 \ \)　　(4)　\( \ 60.5 \ \)　　(5)　\( \ 79.6 \ \)

【ワンポイント解説】

交流回路のインピーダンスの概念がわかっていれば，比較的取り組みやすい問題かと思います。本問でしっかりと理解し，試験本番では確実に得点できるようにしておきましょう。

1.抵抗，コイル，コンデンサのインピーダンス
抵抗\( \ R \ \mathrm {[\Omega ]} \ \)，コイル\( \ L \ \mathrm {[H]} \ \)，コンデンサ\( \ C \ \mathrm {[F]} \ \)があり，電源周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき，それぞれのインピーダンスは，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L \\[ 5pt ] &=&\mathrm {j}2\pi f L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C} \\[ 5pt ] &=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}
\] で求められます。したがって，\( \ RLC \ \)直列回路の合成インピーダンス\( \ \dot Z \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
\dot Z&=&{\dot Z}_{\mathrm {R}}+{\dot Z}_{\mathrm {L}}+{\dot Z}_{\mathrm {C}} \\[ 5pt ] &=&R+\mathrm {j}2\pi f L+\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] &=&R+\mathrm {j}2\pi f L-\mathrm {j}\frac {1}{2\pi f C} （∵\frac {1}{\mathrm {j}}=\frac {1}{\mathrm {j}}\times \frac {\mathrm {j}}{\mathrm {j}}=-\mathrm {j}）\\[ 5pt ] &=&R+\mathrm {j}\left( 2\pi f L-\frac {1}{2\pi f C}\right) \\[ 5pt ] \end{eqnarray}
\] となり，その大きさ\( \ Z \ \mathrm {[\Omega ]} \ \)は三平方の定理より，
\[
\begin{eqnarray}
Z^{2}&=&R^{2}+\left( 2\pi f L-\frac {1}{2\pi f C}\right) ^{2} \\[ 5pt ] Z&=&\sqrt {R^{2}+\left( 2\pi f L-\frac {1}{2\pi f C}\right) ^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められます。

【解答】

解答：(4)
電源の電圧\( \ V=10 \ \mathrm {[V]} \ \)であり，回路を流れる電流\( \ I=0.1 \ \mathrm {[A]} \ \)であるから，回路全体のインピーダンスの大きさ\( \ Z \ \mathrm {[\Omega ]} \ \)は，オームの法則より，
\[
\begin{eqnarray}
Z&=&\frac {V}{I} \\[ 5pt ] &=&\frac {10}{0.1} \\[ 5pt ] &=&100 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。コンデンサの静電容量\( \ C=2 \ \mathrm {[\mu F ]} \ \)，周波数\( \ f=1000 \ \mathrm {[Hz]} \ \)であり，この条件での合成インピーダンスの大きさ\( \ Z \ \mathrm {[\Omega ]} \ \)が等しいから，ワンポイント解説「1.抵抗，コイル，コンデンサのインピーダンス」より，
\[
\begin{eqnarray}
Z&=&\sqrt {R^{2}+\left( \frac {1}{2\pi f C}\right) ^{2}} \\[ 5pt ] Z^{2}&=&R^{2}+\left( \frac {1}{2\pi f C}\right) ^{2} \\[ 5pt ] R^{2}&=&Z^{2}-\left( \frac {1}{2\pi f C}\right) ^{2} \\[ 5pt ] R&=&\sqrt {Z^{2}-\left( \frac {1}{2\pi f C}\right) ^{2}} \\[ 5pt ] &=&\sqrt {100^{2}-\left( \frac {1}{2\times 3.142 \times 1000 \times 2\times 10^{-6} }\right) ^{2}} \\[ 5pt ] &≒&\sqrt {10000-79.57 ^{2}} \\[ 5pt ] &≒&60.6 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

※　コンデンサのインピーダンス約\( \ 80 \ \mathrm {\Omega } \ \)が求められたら，直角三角形の関係\( \ 3:4:5=R:80:100 \ \)から抵抗が約\( \ 60 \ \mathrm {\Omega } \ \)が導出されるので，こちらで解いた方が試験本番では速くて計算ミスも少ないと思います。