《理論》〈電気回路〉[H26:問14]平衡三相交流回路に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

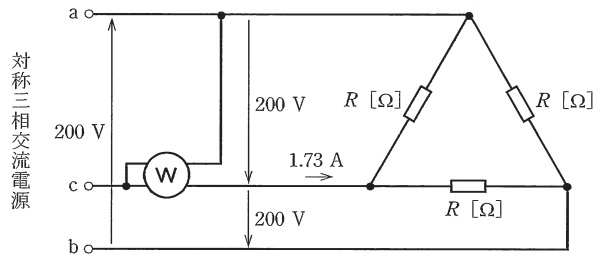
図のように\(200 \ \mathrm {V}\)の対称三相交流電源に抵抗\(R \ \mathrm {[\Omega ]}\)からなる平衡三相負荷を接続したところ，線電流は\(1.73 \ \mathrm {A}\)であった。いま，電力計の電流コイルを\( \ \mathrm {c} \ \)相に接続し，電圧コイル\( \ \mathrm {c}―\mathrm {a} \ \)相間に接続したとき，電力系の指示\(P \ \mathrm {[W]}\)として，最も近い\(P\)の値を次の(1)～(5)のうちから一つ選べ。

ただし，対称三相交流電源の相回転は\(\mathrm {a}\)，\(\mathrm {b}\)，\(\mathrm {c}\)の順とし，電力計の電力損失は無視できるものとする。

(1)　\(200\)　　(2)　\(300\)　　(3)　\(346\)　　(4)　\(400\)　　(5)　\(600\)

【ワンポイント解説】

問題図のような電力計では\(\mathrm {c}-\mathrm {a}\)間電圧と\(\mathrm {c}\)相電流から求められる有効電力が測定されることを知っておかなければなりません。これはある程度問題慣れが必要と思います。ただし，慣れてしまえばすんなり解ける問題なので，点数差が発生しやすい問題と言えます。

【解答】

解答：(2)
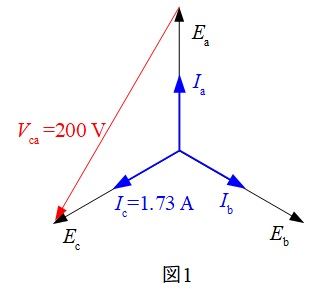
負荷がすべて抵抗であるので電圧と電流の位相は等しい。各相の電圧と電流を\(E_{\mathrm {a}}\)，\(E_{\mathrm {b}}\)，\(E_{\mathrm {c}}\)，\(I_{\mathrm {a}}\)，\(I_{\mathrm {b}}\)，\(I_{\mathrm {c}}\)とすると，ベクトル図は図1のように描ける。また，\(\mathrm {c}-\mathrm {a}\)間電圧\(V_{\mathrm {ca}}\)と\(I_{\mathrm {c}}\)のベクトルは図2のように描け，その位相差は\(\displaystyle \frac {\pi}{6} \ \mathrm {[rad]} \ \)となる。
よって，電力計の指示\(P\)は，
\[
\begin{eqnarray}
P &=&V_{\mathrm {ca}}I_{\mathrm {c}}\cos \frac {\pi}{6} \\[ 5pt ] &=&200\times 1.73 \times \frac {\sqrt{3}}{2} \\[ 5pt ] &≒&300 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。