【問題】
【難易度】★★★★☆(やや難しい)
図1のように,線間電圧\(200 \ \mathrm {V}\),周波数\(50 \ \mathrm {Hz}\)の対称三相交流電源に\(1 \ \Omega \)の抵抗と誘導性リアクタンス\(\displaystyle \frac {4}{3}\Omega \)のコイルとの並列回路からなる平衡三相負荷(\(\mathrm {Y}\)結線)が接続されている。また,スイッチ\(\mathrm {S}\)を介して,コンデンサ\(\mathrm {C}\) (\(\mathrm {\Delta }\)結線) を接続することができるものとする。次の(a)及び(b)の問に答えよ。
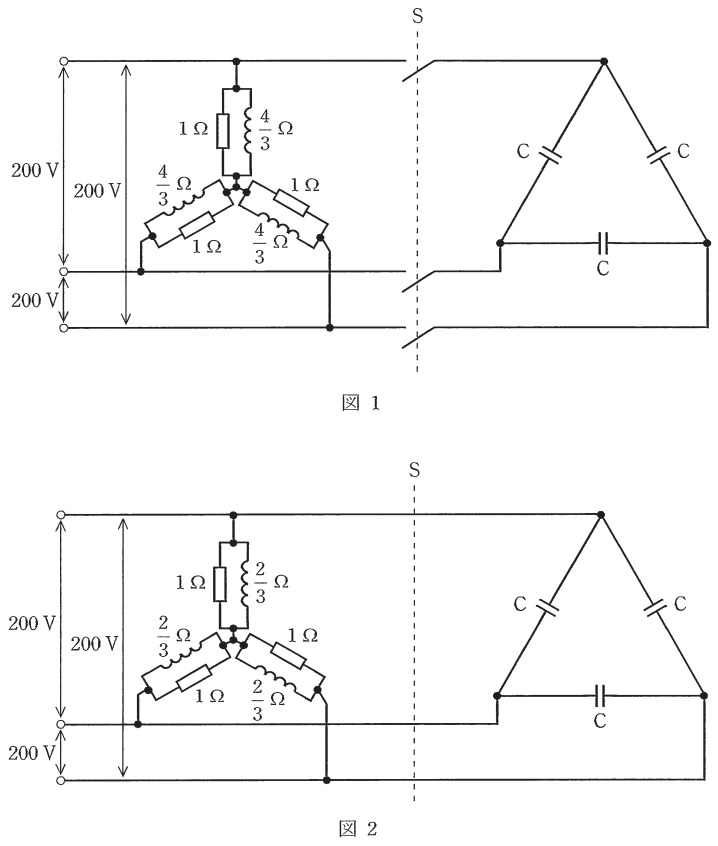
(a) スイッチ\(\mathrm {S}\)が開いた状態において,三相負荷の有効電力\(P\)の値\(\mathrm {[kW]}\)と無効電力\(Q\)の値\(\mathrm {[kvar]}\)の組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccc}
& P & Q \\
\hline
(1) & 40 & 30 \\
\hline
(2) & 40 & 53 \\
\hline
(3) & 80 & 60 \\
\hline
(4) & 120 & 90 \\
\hline
(5) & 120 & 160 \\
\hline
\end{array}
\]
(b) 図2のように三相負荷のコイルの誘導性リアクタンスを\(\displaystyle \frac {2}{3}\Omega \)に置き換え,スイッチ\(\mathrm {S}\)を閉じてコンデンサ\(\mathrm {C}\)を接続する。このとき,電源からみた有効電力と無効電力が図1の場合と同じ値になったとする。コンデンサ\(\mathrm {C}\)の静電容量の値\(\mathrm {[\mu F ]}\)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \(800\) (2) \(1200\) (3) \(2400\) (4) \(4800\) (5) \(7200\)
【ワンポイント解説】
\(\mathrm {\Delta -Y}\)変換を用いる問題です。三種では不平衡負荷の\(\mathrm {\Delta -Y}\)変換が出題されることは少ないですが,非常によく出題される公式なので,確実に覚えておくようにしておきましょう。
1.リアクトルとコンデンサのリアクタンスとサセプタンス
インダクタンスが\(L \ \mathrm {[H]}\)のリアクトルと静電容量\(C \ \mathrm {[F]}\)のコンデンサの各リアクタンス\(X_{\mathrm {L}} \ [\Omega ]\)と\(X_{\mathrm {C}} \ [\Omega ]\)及び各サセプタンス\(b_{\mathrm {L}} \ \mathrm {[S]}\)と\(b_{\mathrm {C}} \ \mathrm {[S]}\)の大きさは,角周波数を\(\omega \ \mathrm {[rad /s]}\)とすると,
\[
\begin{eqnarray}
X_{\mathrm {L}}&=&\mathrm {j}\omega L ,b_{\mathrm {L}}=\frac {1}{\mathrm {j}\omega L } \\[ 5pt ]
X_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C } ,b_{\mathrm {C}}=\mathrm {j}\omega C \\[ 5pt ]
\end{eqnarray}
\]
となります。
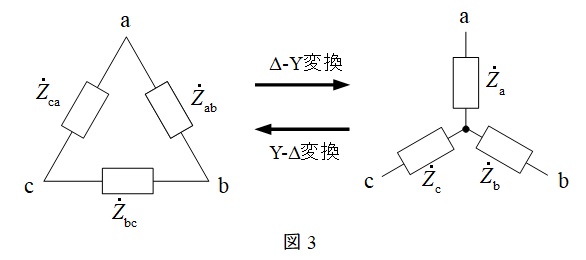
2.\(\Delta -\mathrm {Y}\)変換と\(\mathrm {Y}-\Delta \)変換
①\(\Delta -\mathrm {Y}\)変換
図3において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
\end{eqnarray}
\]
②\(\mathrm {Y}-\Delta \)変換
図3において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ]
{\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ]
{\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ]
\end{eqnarray}
\]
平衡三相回路においては,
\[
{\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}={\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}}
\]
となります。
【関連する「電気の神髄」記事】
【解答】
(a)解答:(1)
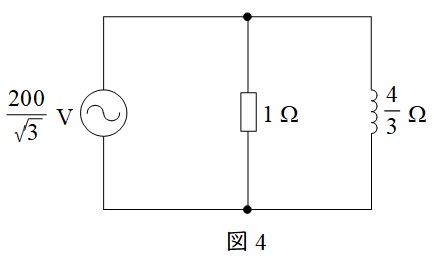
図1の一相分の等価回路は図4のようになる。図4より三相分の有効電力\(P\)は,
\[
\begin{eqnarray}
P &=&3\cdot \frac {V^{2}}{R} \\[ 5pt ]
&=&3\cdot \frac {\displaystyle \left( \frac {200}{\sqrt {3}}\right) ^{2}}{1} \\[ 5pt ]
&=&40000 \ \mathrm {[W]} → 40 \ \mathrm {[kW]}\\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,同様に三相分の無効電力\(Q\)は,
\[
\begin{eqnarray}
Q &=&3\cdot \frac {V^{2}}{X} \\[ 5pt ]
&=&3\cdot \frac {\displaystyle \left( \frac {200}{\sqrt {3}}\right) ^{2}}{\displaystyle \frac {4}{3}} \\[ 5pt ]
&=&30000 \ \mathrm {[var]} → 30 \ \mathrm {[kvar]}\\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(1)
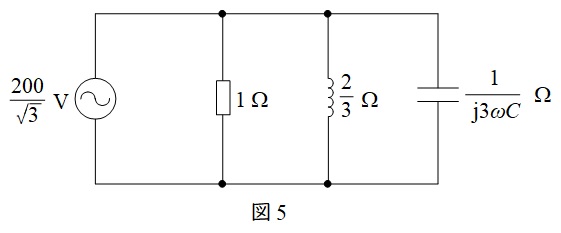
図2において,ワンポイント解説「2.\(\Delta -\mathrm {Y}\)変換と\(\mathrm {Y}-\Delta \)変換」の通り,コンデンサ\(\mathrm {C}\)を\(\Delta -\mathrm {Y}\)変換すると,静電容量は\(3\mathrm {C}\)となるから,一相分の等価回路は図5の通りとなる。
このときの合成インピーダンス(アドミタンス)の大きさが等しくなる。
したがって,その合成アドミタンスは,
\[
\begin{eqnarray}
\frac {3}{4} &=& \frac {3}{2}-3\times 2\pi f \mathrm {C} \\[ 5pt ]
\mathrm {C}&=&\frac {\displaystyle \frac {3}{4}}{3\times 2\pi \times 50} \\[ 5pt ]
&≒&0.000796 \ \mathrm {[F]} → 800 \ \mathrm {[\mu F]}\\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは