《理論》〈電気回路〉[H28:問6]直並列回路の電流比に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

図のような抵抗の直並列回路に直流電圧\( \ E=5 \ \mathrm{V} \ \)を加えたとき，電流比\( \ \displaystyle \frac {I_{2}}{I_{1}} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

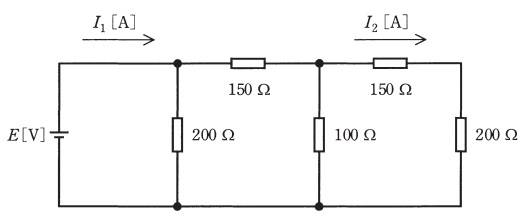
(1)　\( \ 0.1 \ \)　　(2)　\( \ 0.2 \ \)　　(3)　\( \ 0.3 \ \)　　(4)　\( \ 0.4 \ \)　　(5)　\( \ 0.5 \ \)

【ワンポイント解説】

計算がやや面倒ですが，オームの法則とキルヒホッフの法則を使い，順番に丁寧に解けば，それほど難しい問題ではありません。

【解答】

解答：(1)
各部の電圧と抵抗を下図のように指定する。

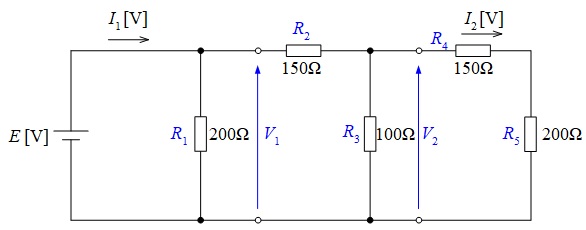
上図において，\( \ V_{2} \ \)は，
\[
\begin{eqnarray}
V_{2}&=&\left( R_{4} +R_{5} \right) I_{2} \\[ 5pt ] &=&\left( 150 +200 \right) I_{2} \\[ 5pt ] &=&350 I_{2}
\end{eqnarray}
\] となる。抵抗\( \ R_{3} \ \)を流れる電流\( \ I_{\mathrm {R}3} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {R}3}&=&\frac {V_{2}}{R_{3}} \\[ 5pt ] &=&\frac {350 I_{2}}{100} \\[ 5pt ] &=&3.5I_{2}
\end{eqnarray}
\] となる。抵抗\( \ R_{2} \ \)を流れる電流\( \ I_{\mathrm {R}2} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {R}2}&=&I_{\mathrm {R}3}+I_{2} \\[ 5pt ] &=&3.5I_{2}+I_{2} \\[ 5pt ] &=&4.5I_{2}
\end{eqnarray}
\] となる。電圧\( \ V_{1} \ \)は，
\[
\begin{eqnarray}
V_{1}&=&V_{2}+R_{2}I_{\mathrm {R}2} \\[ 5pt ] &=&350 I_{2}+150\times 4.5I_{2} \\[ 5pt ] &=&1025 I_{2}
\end{eqnarray}
\] となる。抵抗\( \ R_{1} \ \)を流れる電流\( \ I_{R1} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {R}1}&=&\frac {V_{1}}{R_{1}} \\[ 5pt ] &=&\frac {1025 I_{2}}{200} \\[ 5pt ] &=&5.125 I_{2}
\end{eqnarray}
\] となる。よって，電流\( \ I_{1} \ \)は，
\[
\begin{eqnarray}
I_{1}&=&I_{\mathrm {R}1}+I_{\mathrm {R}2} \\[ 5pt ] &=&5.125 I_{2}+4.5I_{2} \\[ 5pt ] &=&9.625 I_{2} \\[ 5pt ] \end{eqnarray}
\] となるので，電流比\( \ \displaystyle \frac {I_{2}}{I_{1}} \ \)は，
\[
\begin{eqnarray}
\frac {I_{2}}{I_{1}}=\frac {1}{9.625}&≒&0.1 \\[ 5pt ] \end{eqnarray}
\] と求められる。

[別解]

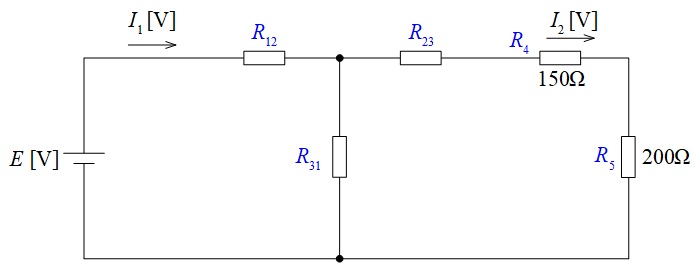
\( \ R_{1}=200 \ \Omega \ \)，\( \ R_{2}=150 \ \Omega \ \)，\( \ R_{3}=100 \ \Omega \ \)の抵抗を\( \ \Delta -\mathrm {Y} \ \)変換した回路を下図のように定義すると，
\[
\begin{eqnarray}
R_{12}&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}+R_{3}} \\[ 5pt ] &=&\frac {200\times 150}{200+150+100} \\[ 5pt ] &≒&66.667 \ [\Omega] \\[ 5pt ] R_{23}&=&\frac {R_{2}R_{3}}{R_{1}+R_{2}+R_{3}} \\[ 5pt ] &=&\frac {150\times 100}{200+150+100} \\[ 5pt ] &≒&33.333 \ [\Omega] \\[ 5pt ] R_{31}&=&\frac {R_{3}R_{1}}{R_{1}+R_{2}+R_{3}} \\[ 5pt ] &=&\frac {100\times 200}{200+150+100} \\[ 5pt ] &≒&44.444 \ [\Omega] \\[ 5pt ] \end{eqnarray}
\] となる。よって，分流の法則により\( \ R_{4} \ \)に流れる電流の大きさ\( \ I_{2} \ \)は，
\[
\begin{eqnarray}
I_{2}&=&\frac {R_{31}}{R_{31}+R_{23}+R_{4}+R_{5}}I_{1} \\[ 5pt ] &=&\frac {44.444}{44.444+33.333+150+200}I_{1} \\[ 5pt ] &≒&0.1I_{1} \\[ 5pt ] \end{eqnarray}
\] と求められる。