《理論》〈電気回路〉[H24:問9]RL回路の過渡現象に関する論説問題

【問題】

【難易度】★★★☆☆（普通）

図のように，直流電圧\( \ E \ \mathrm {[V]} \ \)の電源，\( \ R \ \mathrm {[\Omega ]} \ \)の抵抗，インダクタンス\( \ L \ \mathrm {[H]} \ \)のコイル，スイッチ\( \ \mathrm {S}_{1} \ \)と\( \ \mathrm {S}_{2} \ \)からなる回路がある。電源の内部インピーダンスは零とする。時刻\( \ t=t_{1} \ \mathrm {[s]} \ \)でスイッチ\( \ \mathrm {S}_{1} \ \)を閉じ，その後，時定数\( \ \displaystyle \frac {L}{R} \ \mathrm {[s]} \ \)に比べて十分に時間が経過した時刻\( \ t=t_{2} \ \mathrm {[s]} \ \)でスイッチ\( \ \mathrm {S}_{2} \ \)を閉じる。このとき，電源から流れ出る電流\( \ i \ \mathrm {[A]} \ \)の波形を示す図として，最も近いものを次の(1)～(5)のうちから一つ選べ。

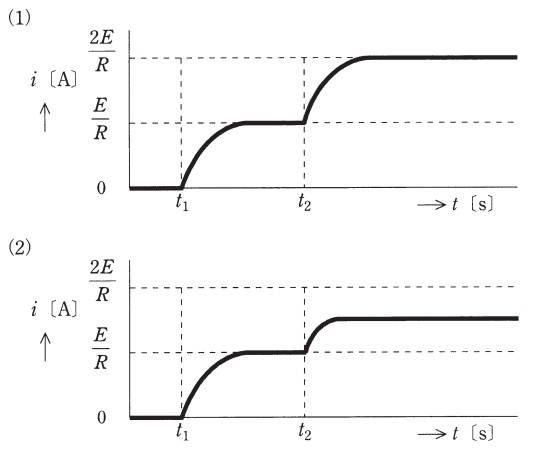
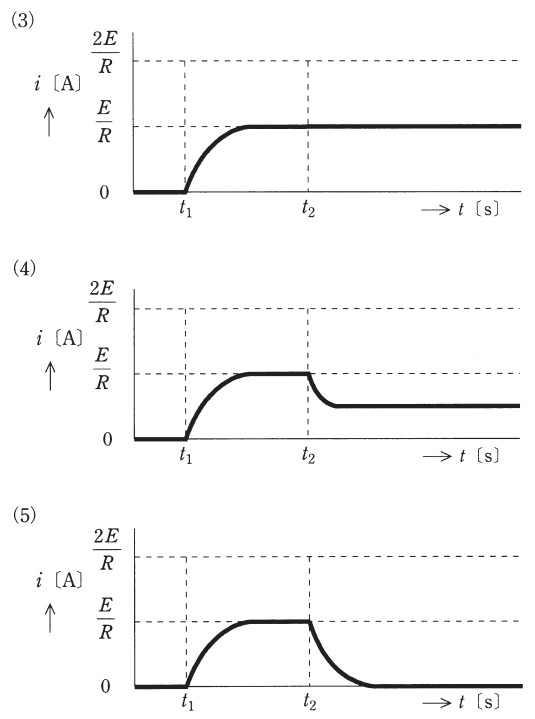
【ワンポイント解説】

過渡現象を理解していればそれほど難易度の高い問題ではありませんが，スイッチ\( \ \mathrm {S}_{2} \ \)を閉じた後の状態がどうなるかをきちんと理解していないと引っ掛かってしまいます。回路図を描き，電流がどう流れるかを考えて波形をイメージするようにしましょう。

1.過渡現象におけるリアクトルの過渡状態と定常状態
① 過渡状態
リアクトルに流れる電流値を維持しようとする働きをします。したがって，リアクトルに電圧を印加した瞬間はほとんど電流は流れないので，開放として考えます。

② 定常状態
電圧を印加して十分時間が経過した後は，リアクトルの抵抗はほぼ零になります。したがって，短絡として考えます。

【解答】

解答：(3)
ワンポイント解説「1.過渡現象におけるリアクトルの過渡状態と定常状態」の通り，時刻\( \ t=t_{1} \ \mathrm {[s]} \ \)でスイッチ\( \ \mathrm {S}_{1} \ \)を閉じた瞬間は\( \ L \ \)は開放と考えることができるので電流が流れない。
その後，十分時間が経った定常状態では\( \ L \ \)は短絡と考えることができるので，回路図は図1のようになる。この時，電源を流れる電流は，
\[
\begin{eqnarray}
i&=&\frac {E}{R} \\[ 5pt ] \end{eqnarray}
\] となる。

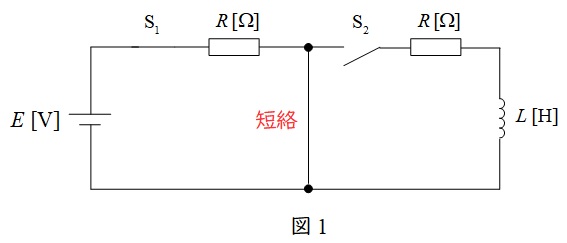
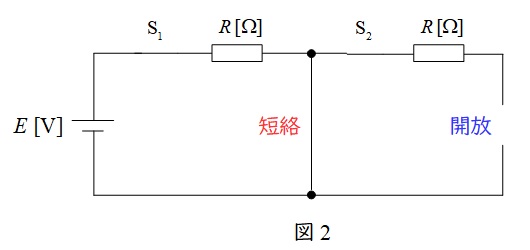
次に，時刻\( \ t=t_{2} \ \mathrm {[s]} \ \)でスイッチ\( \ \mathrm {S}_{2} \ \)を閉じると，回路図は図2のようになる。
図2より，\( \ t=t_{2} \ \mathrm {[s]} \ \)以降も中央の\( \ L \ \)は短絡と考えることができるので，電流は\( \ \mathrm {S}_{2} \ \)側を流れない。したがって，電源を流れる電流は\( \ \displaystyle i=\frac {E}{R} \ \)のままとなる。