【問題】
【難易度】★★★☆☆(普通)
図のように,十分大きい平らな金属板で覆われた床と平板電極で作られる空気コンデンサが二つ並列接続されている。二つの電極は床と平行であり,それらの面積は左側が\( \ A_{1}=10^{-3} \ {\mathrm {m}}^{2} \ \),右側が\( \ A_{2}=10^{-2} \ {\mathrm {m}}^{2} \ \)である。床と各電極の間隔は左側が\( \ d=10^{-3} \ \mathrm {m} \ \)で固定,右側が\( \ x \ \mathrm { [ m ] } \ \)で可変,直流電源電圧は\( \ V_{0}=1000 \ \mathrm {V} \ \)である。次の(a)及び(b)の問に答えよ。
ただし,空気の誘電率を\( \ \varepsilon =8.85\times 10^{-12} \ \mathrm {F/m} \ \)とし,静電容量を考える際にコンデンサの端効果は無視できるものとする。
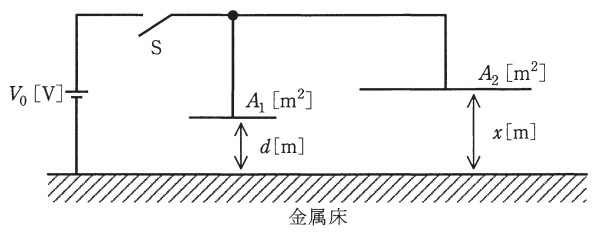
(a) まず,右側の\( \ x \ \mathrm { [ m ] } \ \)を\( \ d \ \mathrm { [ m ] } \ \)と設定し,スイッチ\( \ \mathrm {S} \ \)を一旦閉じてから開いた。このとき,二枚の電極に蓄えられる合計電荷\( \ Q \ \)の値\( \ \mathrm { [ C ] } \ \)として最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \(8.0\times 10^{-9}\) (2) \(1.6\times 10^{-8}\) (3) \(9.7\times 10^{-8}\)
(4) \(1.9\times 10^{-7}\) (5) \(1.6\times 10^{-6}\)
(b) 上記(a)の操作の後,徐々に\( \ x \ \)を増していったところ,\( \ x=3.0\times 10^{-3} \ \mathrm {m} \ \)のときに左側の電極と床との間に火花放電が生じた。左側のコンデンサの空隙の絶縁破壊電圧\( \ V \ \)の値\( \ \mathrm { [ V ] } \ \)として最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \(3.3\times 10^{2}\) (2) \(2.5\times 10^{3}\) (3) \(3.0\times 10^{3}\)
(4) \(5.1\times 10^{3}\) (5) \(3.0\times 10^{4}\)
【ワンポイント解説】
平行平板コンデンサの基本公式を理解していれば,問題なく解答できる問題です。理論科目合格するためには本問は完答したいところです。
1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係
平行平板コンデンサにおいて,蓄えられる電荷\( \ Q \ \mathrm {[C]} \ \)と静電容量\( \ C \ \mathrm {[F]} \ \)及び電圧\( \ V \ \mathrm {[V]} \ \)には,
\[
\begin{eqnarray}
Q &=&CV \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
2.平行平板コンデンサの静電容量\( \ C \ \)
平行平板コンデンサの静電容量\( \ C \ \mathrm {[F]} \ \)は,真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \),極板の面積を\( \ S \ \mathrm {[m^{2}]} \ \),極板間の距離を\( \ d \ \mathrm {[m]} \ \)とすると,
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{0}S}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。平行平板コンデンサの間に比誘電率\( \ \varepsilon _{\mathrm {r}} \ \)の誘電体を挿入すると,
\[
\begin{eqnarray}
C &=&\frac {\varepsilon _{\mathrm {r}} \varepsilon _{0}S}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.コンデンサの合成静電容量
静電容量\( \ C_{1} \ \mathrm {[F]} \ \)と\( \ C_{2} \ \mathrm {[F]} \ \)の合成静電容量\( \ C \ \mathrm {[F]} \ \)は,
並列接続時:\( \ C=C_{1}+C_{2} \ \)
直列接続時:\( \ \displaystyle C=\frac {1}{\displaystyle \frac {1}{C_{1}}+\frac {1}{C_{2}}}=\frac {C_{1}C_{2}}{C_{1}+C_{2}} \ \)
となります。
【関連する「電気の神髄」記事】
【解答】
(a)解答:(3)
題意に沿って図を描くと図1のようになる。図1に示すように,左側のコンデンサの静電容量を\( \ C_{1} \ \mathrm {[F]} \ \),右側のコンデンサの静電容量を\( \ C_{2} \ \mathrm {[F]} \ \)とすると,ワンポイント解説「2.平行平板コンデンサの静電容量\( \ C \ \)」の通り,
\[
\begin{eqnarray}
C_{1}&=&\frac {\varepsilon A_{1}}{d} \\[ 5pt ]
&=&\frac {8.85\times 10^{-12}\times 10^{-3}}{10^{-3}} \\[ 5pt ]
&=&8.85\times 10^{-12} \ \mathrm {[F]} \\[ 5pt ]
C_{2}&=&\frac {\varepsilon A_{2}}{x} \\[ 5pt ]
&=&\frac {8.85\times 10^{-12}\times 10^{-2}}{10^{-3}} \\[ 5pt ]
&=&8.85\times 10^{-11} \ \mathrm {[F]} \\[ 5pt ]
\end{eqnarray}
\]
となる。並列のコンデンサの合成静電容量は,ワンポイント解説「3.コンデンサの合成静電容量」の通り\( \ C_{1} + C_{2} \ \)であるので,二枚の電極に蓄えられる合計電荷\( \ Q \ \mathrm {[C]} \ \)は,ワンポイント解説「1.電荷\( \ Q \ \)と静電容量\( \ C \ \)及び電圧\( \ V \ \)の関係」の通り,
\[
\begin{eqnarray}
Q&=&\left( C_{1} + C_{2} \right) V_{0} \\[ 5pt ]
&=&\left( 8.85\times 10^{-12} + 8.85\times 10^{-11} \right) \times 1 \ 000 \\[ 5pt ]
&=&9.735\times 10^{-8} → 9.7\times 10^{-8} \ \mathrm {[C]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
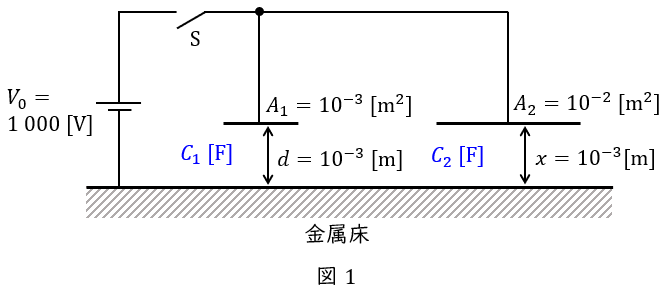
(b)解答:(2)
図2のように,\( \ x=3.0\times 10^{-3} \ \mathrm {[m]} \ \)とした時の静電容量\( \ C_{2}^{\prime } \ \mathrm {[F]} \ \)は,
\[
\begin{eqnarray}
C_{2}^{\prime}&=&\frac {\varepsilon A_{2}}{x} \\[ 5pt ]
&=&\frac {8.85\times 10^{-12}\times 10^{-2}}{3.0\times 10^{-3}} \\[ 5pt ]
&=&2.95\times 10^{-11} \ \mathrm {[F]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ C_{1} \ \)と\( \ C_{2}^{\prime } \ \)の合計静電容量\( \ C \ \mathrm {[F]} \ \)は,
\[
\begin{eqnarray}
C&=&C_{1} + C_{2}^{\prime } \\[ 5pt ]
&=&8.85\times 10^{-12}+2.95\times 10^{-11} \\[ 5pt ]
&=&3.835\times 10^{-11} \ \mathrm {[F]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,絶縁破壊発生時にコンデンサの両端に加わる電圧\( \ V \ \mathrm {[V]} \ \)は,蓄えられる電荷量の合計が変化しないことを考慮すると,
\[
\begin{eqnarray}
V&=&\frac {Q}{C} \\[ 5pt ]
&=&\frac {9.735\times 10^{-8} }{3.835\times 10^{-11}} \\[ 5pt ]
&≒&2.54\times 10^{3} \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは