Contents
【問題】
【難易度】★★★☆☆(普通)
振幅変調について,次の(a)及び(b)の問に答えよ。
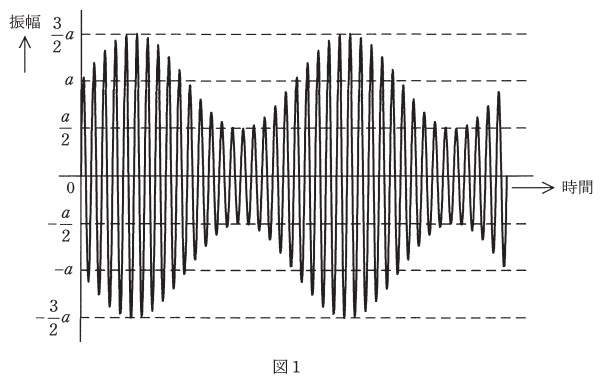
(a) 図1の波形は,正弦波である信号波によって搬送波の振幅を変化させて得られた変調波を表している。この変調波の変調度の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 0.33 \ \) (2) \( \ 0.5 \ \) (3) \( \ 1.0 \ \) (4) \( \ 2.0 \ \) (5) \( \ 3.0 \ \)
(b) 次の文章は,直線検波回路に関する記述である。
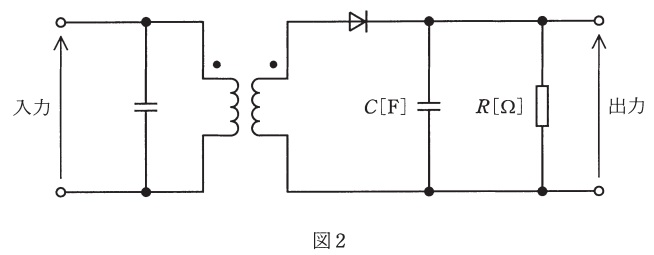
振幅変調した変調波の電圧を,図2の復調回路に入力して復調したい。コンデンサ\( \ C \ \mathrm { [ F ] } \ \)と抵抗\( \ R \ \mathrm { [ \Omega ] } \ \)を並列接続した合成インピーダンスの両端電圧に求められることは,信号波の成分が\( \ \fbox { (ア) } \ \)ことと,搬送波の成分が\( \ \fbox { (イ) } \ \)ことである。そこで,合成インピーダンスの大きさは,信号波の周波数に対してほぼ抵抗\( \ R \ \mathrm { [ \Omega ] } \ \)となり,搬送波の周波数に対して十分に\( \ \fbox { (ウ) } \ \)なくてはならない。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{cccc}
& (ア) & (イ) & (ウ) \\
\hline
(1) & あ る & なくなる & 大きく \\
\hline
(2) & あ る & なくなる & 小さく \\
\hline
(3) & なくなる & あ る & 小さく \\
\hline
(4) & なくなる & なくなる & 小さく \\
\hline
(5) & なくなる & あ る & 大きく \\
\hline
\end{array}
\]
【ワンポイント解説】
内容は電気というよりも無線工学に近い内容です。参考程度に確認しておいて下さい。本問の図1は図3に示すように,振幅\( \ \displaystyle \frac {a}{2} \ \)の信号波によって振幅\( \ a \ \)の搬送波を変化させて得られたものとなります。
1.無線通信における信号の伝送
図3に示すように,無線通信おいて,信号波と呼ばれる送りたい情報を周波数のより高い搬送波と呼ばれる信号を送信機によって合成し,変調波を作って送信します。
搬送波の振幅に対する信号波の振幅の大きさ\( \ \displaystyle \frac {a_{1}}{a_{2}} \ \)を変調波の変調度といいます。
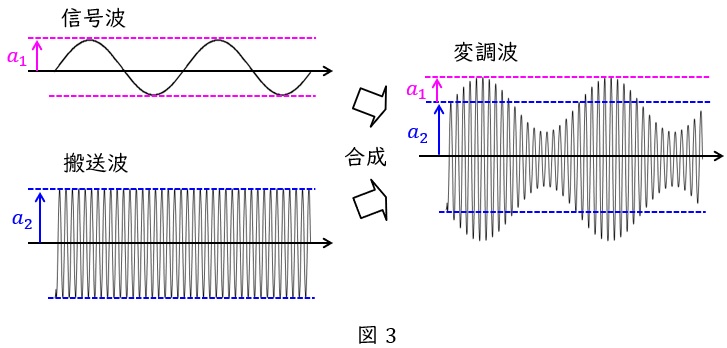
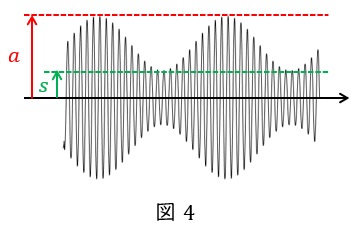
もし,変調波のみが与えられている場合には変調波の振幅の最大値\( \ a \ \)及び最小値\( \ s \ \)であるとき,\( \ \displaystyle \frac {a-s}{a+s} \ \)でも求めることができます。
【解答】
(a)解答:(2)
図1より,変調波の振幅の最大値が\( \ \displaystyle \frac {3}{2}a \ \),最小値が\( \ \displaystyle \frac {a}{2} \ \)であるから,変調度は,ワンポイント解説「1.無線通信における信号の伝送」の通り,
\[
\frac {\displaystyle \frac {3}{2}a-\frac {a}{2}}{\displaystyle \frac {3}{2}a+\frac {a}{2}}=0.5
\]
と求められる。
(b)解答:(2)
復調する場合に求められるのは,きちんと入力信号を出力できることです。
したがって,復調回路では信号波は(ア)あることと搬送波が(イ)なくなることが求められます。
図2においては,信号側成分が抵抗に,搬送波成分がコンデンサ側に行くようにすれば理想的な状態となります。搬送波成分が抵抗側に行かないようにするためには,コンデンサのリアクタンス\( \ \displaystyle \frac {1}{\mathrm {j}2\pi fC} \ \)が十分に(ウ)小さく,理想的にはほぼゼロになるように設定し,抵抗側へ流れないようにすることが求められます。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは