《理論》〈電磁気〉[H28:問3]ビオ・サバールの法則に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

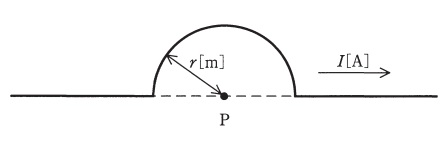
図のように，長い線状導体の一部が点\( \ \mathrm {P} \ \)を中心とする半径\( \ r \ \mathrm {[m]} \ \)の半円形になっている。この導体に電流\( \ I \ \mathrm {[A]} \ \)を流すとき，点\( \ \mathrm {P} \ \)に生じる磁界の大きさ\( \ H \ \mathrm {[A/m]} \ \)はビオ・サバールの法則より求めることができる。\( \ H \ \)を表す式として正しいものを，次の(1)～(5)のうちから一つ選べ。

(1)　\(\displaystyle \frac {I}{2\pi r}\)　　(2)　\(\displaystyle \frac {I}{4 r}\)　　(3)　\(\displaystyle \frac {I}{\pi r}\)　　(4)　\(\displaystyle \frac {I}{2r}\)　　(5)　\(\displaystyle \frac {I}{r}\)

【ワンポイント解説】

ビオ・サバールの法則は比較的複雑な公式と言えます。しかしながら，法則なので覚える必要があります。本問の場合，ビオ・サバールの法則の公式自体を覚えていなくても，円形回路により発生する磁界を求める公式を覚えていれば正答を導き出すことは可能です。

1.ビオ・サバールの法則
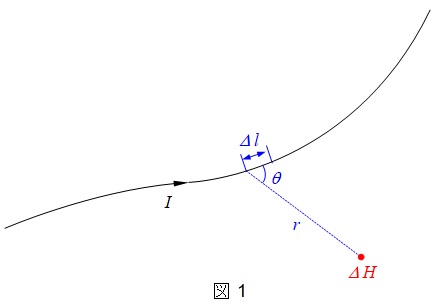
図1に示すように，微小な長さ\( \ \Delta l \ \)に流れる電流\( \ I \ \)が，距離\( \ r \ \)離れた場所に作る磁界\( \ \Delta H \ \)は，
\[
\begin{eqnarray}
\Delta H=\frac {I \Delta l}{4\pi r^{2}}\sin \theta \\[ 5pt ] \end{eqnarray}
\] となります。

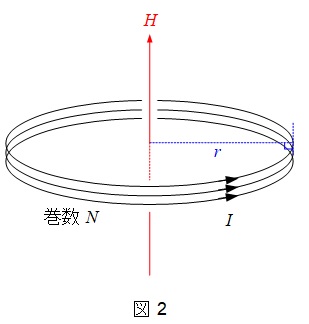
次に，図2に示すような半径\( \ r \ \)，巻数\( \ N \ \)のコイルが中心部に作る磁界の大きさ\( \ H \ \)は，長さの合計が\( \ 2\pi r \ \)，\( \ \displaystyle \theta =\frac {\pi}{2} \ \)であるから，
\[
\begin{eqnarray}
H&=&\frac {NI \cdot 2\pi r}{4\pi r^{2}}\sin \frac {\pi }{2} \\[ 5pt ] &=&\frac {NI}{2r}
\end{eqnarray}
\] となります。

【解答】

解答：(2)
本問は巻数\( \ \displaystyle N=\frac {1}{2} \ \)のコイルが作る磁界の大きさに等しいので，
\[
\begin{eqnarray}
H&=&\frac {NI}{2r} \\[ 5pt ] &=&\frac {\displaystyle \frac {1}{2}I}{2r} \\[ 5pt ] &=&\frac {I}{4r} \\[ 5pt ] \end{eqnarray}
\] と求められる。