Contents
【問題】
【難易度】★★★☆☆(普通)
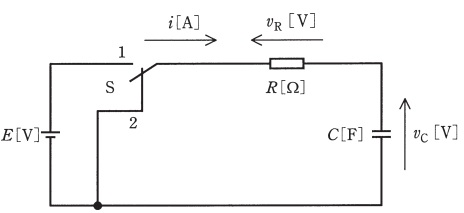
図のように,電圧\( \ E \ \mathrm {[ V ] } \ \)の直流電源,スイッチ\( \ \mathrm {S} \ \),\( \ R \ \mathrm {[ \Omega ] } \ \)の抵抗及び静電容量\( \ C \ \mathrm {[ F ] } \ \)のコンデンサからなる回路がある。この回路において,スイッチ\( \ \mathrm {S} \ \)を\( \ 1 \ \)側に接続してコンデンサを十分に充電した後,時刻\( \ t=0 \ \mathrm {s} \ \)でスイッチ\(\mathrm {S}\)を\( \ 1 \ \)側から\( \ 2 \ \)側に切り換えた。\( \ 2 \ \)側に切り換えた以降の記述として,誤っているものを次の(1)~(5)のうちから一つ選べ。
ただし,自然対数の底は,\( \ 2.718 \ \)とする。
(1) 回路の時定数は,\( \ C \ \)の値\( \ \mathrm {[ F ] } \ \)に比例する。
(2) コンデンサの端子電圧\( \ v_{\mathrm {C}} \ \mathrm {[ V ] } \ \)は,\( \ R \ \)の値\( \ \mathrm {[ \Omega ] } \ \)が大きいほど緩やかに減少する。
(3) 時刻\( \ t=0 \ \mathrm {s} \ \)から回路の時定数だけ時間が経過すると,コンデンサの端子電圧\( \ v_{\mathrm {C}} \ \mathrm {[ V ] } \ \)は直流電源の電圧\( \ E \ \mathrm {[ V ] } \ \)の\( \ 0.368 \ \)倍に減少する。
(4) 抵抗の端子電圧\( \ v_{\mathrm {R}} \ \mathrm {[ V ] } \ \)の極性は,切り換え前(コンデンサ充電中)と逆になる。
(5) 時刻\( \ t=0 \ \mathrm {s} \ \)における回路の電流\( \ i \ \mathrm {[ A ] } \ \)は,\( \ C \ \)の値\( \ \mathrm {[ F ] } \ \)に関係する。
【ワンポイント解説】
過渡現象は回路の微分方程式を解いて求めますが,三種の場合はその結果を定量的ではなく定性的に理解していれば問題ありません。
スイッチの切り換え前後で電流の流れがどうなるかよく理解しておいて下さい。
1.過渡現象におけるリアクトルの過渡状態と定常状態
① 過渡状態
リアクトルに流れる電流値を維持しようとする働きをします。したがって,リアクトルに電圧を印加した瞬間はほとんど電流は流れないので,開放として考えます。
② 定常状態
電圧を印加して十分時間が経過した後は,リアクトルの抵抗はほぼ零になります。したがって,短絡として考えます。
2.過渡現象におけるコンデンサの過渡状態と定常状態
① 過渡状態
コンデンサに蓄えられている電荷が零であるので,電流がものすごく流れやすい状態,すなわち短絡として考えます。
② 定常状態
コンデンサに十分に電荷が蓄えられているので,電流をこれ以上蓄えようとしない,すなわち開放として考えます。
3.時定数
過渡現象におけるリアクトルやコンデンサの電圧の導出は微分方程式の計算を伴うため二種以上の範囲となりますが,図1-1や図2-1のような回路が与えられると,図1-1のリアクトル電圧\( \ V_{\mathrm {L}} \ \mathrm {[V]} \ \)及び回路を流れる電流\( \ I_{\mathrm {L}} \ \mathrm {[A]} \ \),図2-1のコンデンサ電圧\( \ V_{\mathrm {C}} \ \mathrm {[V]} \ \)及び回路を流れる電流\( \ I_{\mathrm {C}} \ \mathrm {[A]} \ \)はそれぞれ,
\[
\begin{eqnarray}
V_{\mathrm {L}} &=&E\mathrm {e}^{-\frac {R}{L}t} \\[ 5pt ]
I_{\mathrm {L}} &=&\frac {E}{R}\left( 1-\mathrm {e}^{-\frac {R}{L}t}\right) \\[ 5pt ]
V_{\mathrm {C}} &=&E\left( 1-\mathrm {e}^{-\frac {t}{CR}}\right) \\[ 5pt ]
I_{\mathrm {C}} &=&\frac {E}{R}\mathrm {e}^{-\frac {t}{CR}} \\[ 5pt ]
\end{eqnarray}
\]
で与えられ,\( \ \displaystyle t=\frac {L}{R} \ \)及び\( \ t=CR \ \)となる時間を時定数\( \ \tau \ \)と呼びます。
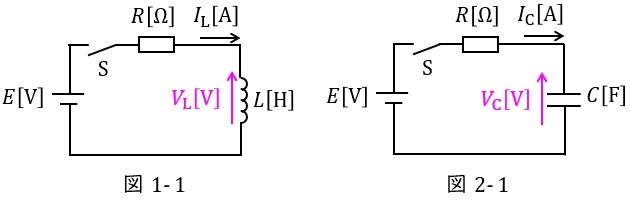
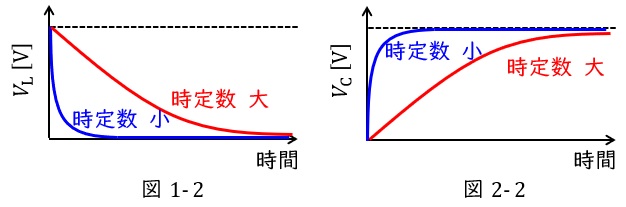
時定数\( \ \tau \ \)が大きくなると図1-2及び図2-2のように経過時間に対し,収束するまでの時間が遅くなります。
【解答】
解答:(5)
(1):正しい
ワンポイント解説「3.時定数」の通り,時定数は\( \ \tau =RC \ \)で表され,時定数は静電容量\( \ C \ \mathrm {[F]} \ \)に比例します。
(2):正しい
ワンポイント解説「3.時定数」の通り,時定数は\( \ \tau =RC \ \)なので,\( \ R \ \)が大きいほど\( \ v_{\mathrm {C}} \ \)は緩やかに減少するようになります。
(3):正しい
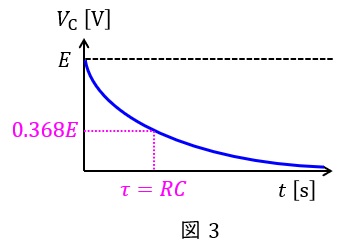
スイッチ\( \ \mathrm {S} \ \)を\( \ 1 \ \)側から\( \ 2 \ \)側に切り換えた後,コンデンサに蓄えらえていた電荷が放電され,図3に示すように電圧は変化します。
このとき時定数だけ時間が経過したときは端子電圧の大きさは\( \ 0.368 \ \)倍に減少します。
※定量的に示すと以下の通りとなります。
\[
\begin{eqnarray}
v_{\mathrm {C}}( RC ) &=&E\mathrm {e}^{-\frac {RC}{RC}} \\[ 5pt ]
&=&E\mathrm {e}^{-1} \\[ 5pt ]
&≒&0.368E \\[ 5pt ]
\end{eqnarray}
\]
(4):正しい
切り換え前後で電流の向きが逆となるため,\( \ v_{\mathrm {R}} \ \)の極性も逆となります。
(5):誤り
ワンポイント解説「2.過渡現象におけるコンデンサの過渡状態と定常状態」の通り,\( \ t=0 \ \)の過渡状態において,コンデンサに蓄えられている電荷が一気に放出されるので,電流は\( \ \displaystyle i ( 0 ) =-\frac {E}{R} \ \)となり,\( \ C \ \)の値に無関係となります。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは