Contents
【問題】
【難易度】★★★★☆(やや難しい)
図は,抵抗\( \ R_{\mathrm {ab}} \ \mathrm {[k\Omega ]} \ \)のすべり抵抗器,抵抗\( \ R_{\mathrm {d}} \ \mathrm {[k\Omega ]} \ \),抵抗\( \ R_{\mathrm {e}} \ \mathrm {[k\Omega ]} \ \)と直流電圧\( \ E_{\mathrm {s}}=12 \ \mathrm {V} \ \)の電源を用いて,端子\( \ \mathrm {H} \ \),\( \ \mathrm {G} \ \)間に接続した未知の直流電圧\( \ \mathrm {[V]} \ \)を測るための回路である。次の(a)及び(b)の問に答えよ。
ただし,端子\( \ \mathrm {G} \ \)を電位の基準\( \ \left( 0 \ \mathrm {V}\right) \ \)とする。
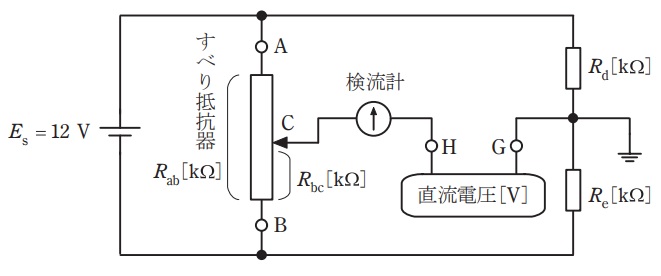
(a) 抵抗\( \ R_{\mathrm {d}}=5 \ \mathrm {k\Omega } \ \),抵抗\( \ R_{\mathrm {e}}=5 \ \mathrm {k\Omega } \ \)として,直流電圧\( \ 3 \ \mathrm {V} \ \)の電源の正極を端子\( \ \mathrm {H} \ \)に,負極を端子\( \ \mathrm {G} \ \)に接続した。すべり抵抗器の接触子\( \ \mathrm {C} \ \)の位置を調整して検流計の電流を零にしたところ,すべり抵抗器の端子\( \ \mathrm {B} \ \)と接触子\( \ \mathrm {C} \ \)間の抵抗\( \ R_{\mathrm {bc}}=18 \ \mathrm {k\Omega } \ \)となった。すべり抵抗器の抵抗\( \ R_{\mathrm {ab}} \ \mathrm {[k\Omega ]} \ \)の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 18 \ \) (2) \( \ 24 \ \) (3) \( \ 36 \ \) (4) \( \ 42 \ \) (5) \( \ 50 \ \)
(b) 次に,直流電圧\( \ 3 \ \mathrm {V} \ \)の電源を取り外し,未知の直流電圧\( \ E_{\mathrm {x}} \ \mathrm {[V]} \ \)の電源を端子\( \ \mathrm {H} \ \),\( \ \mathrm {G} \ \)間に接続した。ただし,端子\( \ \mathrm {G} \ \)から見た端子\( \ \mathrm {H} \ \)の電圧を\( \ E_{\mathrm {x}} \ \mathrm {[V]} \ \)とする。
抵抗\( \ R_{\mathrm {d}}=2 \ \mathrm {k\Omega } \ \),抵抗\( \ R_{\mathrm {e}}=22 \ \mathrm {k\Omega } \ \)としてすべり抵抗器の接触子\( \ \mathrm {C} \ \)の位置を調整し,すべり抵抗器の端子\( \ \mathrm {B} \ \)と接触子\( \ \mathrm {C} \ \)間の抵抗\( \ R_{\mathrm {bc}}=12 \ \mathrm {k\Omega } \ \)としたときに,検流計の電流が零となった。このときの\( \ E_{\mathrm {x}} \ \mathrm {[V]} \ \)の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ -5 \ \) (2) \( \ -3 \ \) (3) \( \ 0 \ \) (4) \( \ 3 \ \) (5) \( \ 5 \ \)
【ワンポイント解説】
すべり抵抗器に関する演算の問題です。
設問(a)と(b)の解法がほぼ同じで関連性が非常に高く,解ける人は両方解けて,解けない人は両方解けない,とても差がつきやすい問題です。
すべり抵抗器は長さと抵抗値が比例する抵抗器なので,それを理解していれば基本公式以外の特別な公式は不要となります。
1.分圧・分流の法則
①分圧の法則
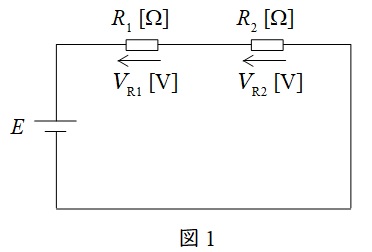
図1に示した直列回路において,各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ]
V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ]
\end{eqnarray}
\]
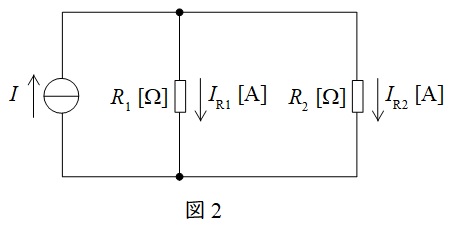
②分流の法則
図2に示した並列回路において,各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ]
I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(a)解答:(2)
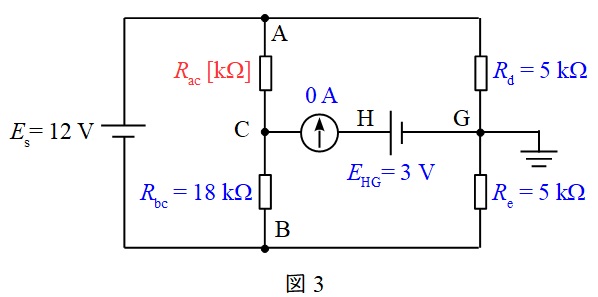
題意に沿って,回路図を描くと図3のようになる。
図3において,\( \ R_{\mathrm {d}}=R_{\mathrm {e}}=5 \ \mathrm {[k\Omega ]} \ \)であるから,\( \ R_{\mathrm {d}} \ \)にかかる電圧\( \ V_{\mathrm {d}} \ \mathrm {[V]} \ \)及び\( \ R_{\mathrm {e}} \ \)にかかる電圧\( \ V_{\mathrm {e}} \ \mathrm {[V]} \ \)は,ワンポイント解説「1.分圧・分流の法則」より,
\[
\begin{eqnarray}
V_{\mathrm {d}}&=&\frac {R_{\mathrm {d}}}{R_{\mathrm {d}}+R_{\mathrm {e}}}E_{\mathrm {s}} \\[ 5pt ]
&=&\frac {5}{5+5}\times 12 \\[ 5pt ]
&=&6 \ \mathrm {[V]} \\[ 5pt ]
V_{\mathrm {e}}&=&\frac {R_{\mathrm {e}}}{R_{\mathrm {d}}+R_{\mathrm {e}}}E_{\mathrm {s}} \\[ 5pt ]
&=&\frac {5}{5+5}\times 12 \\[ 5pt ]
&=&6 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。端子\( \ \mathrm {G} \ \)が接地され,\( \ V_{\mathrm {G}}=0 \ \mathrm {[V]} \ \)であるので,端子\( \ \mathrm {A} \ \)の電位\( \ V_{\mathrm {A}} \ \mathrm {[V]} \ \)及び端子\( \ \mathrm {B} \ \)の電位\( \ V_{\mathrm {B}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {A}}&=&V_{\mathrm {G}}+V_{\mathrm {d}} \\[ 5pt ]
&=&0+6 \\[ 5pt ]
&=&6 \ \mathrm {[V]} \\[ 5pt ]
V_{\mathrm {B}}&=&V_{\mathrm {G}}-V_{\mathrm {e}} \\[ 5pt ]
&=&0-6 \\[ 5pt ]
&=&-6 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,端子\( \ \mathrm {H} \ \)の電位\( \ V_{\mathrm {H}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {H}}&=&V_{\mathrm {G}}+E_{\mathrm {HG}} \\[ 5pt ]
&=&0+3 \\[ 5pt ]
&=&3 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となり,端子\( \ \mathrm {C} \ \)の電位\( \ V_{\mathrm {C}} \ \)も\( \ 3 \ \mathrm {V} \ \)となる。以上から,すべり抵抗器に分圧の法則を適用すれば,
\[
\begin{eqnarray}
V_{\mathrm {C}}-V_{\mathrm {B}}&=&\frac {R_{\mathrm {bc}}}{R_{\mathrm {ac}}+R_{\mathrm {bc}}}E_{\mathrm {s}} \\[ 5pt ]
&=&\frac {R_{\mathrm {bc}}}{R_{\mathrm {ab}}}E_{\mathrm {s}} \\[ 5pt ]
R_{\mathrm {ab}}&=&R_{\mathrm {bc}}\frac {E_{\mathrm {s}}}{V_{\mathrm {C}}-V_{\mathrm {B}}} \\[ 5pt ]
&=&18\times \frac {12}{3-\left(-6\right) } \\[ 5pt ]
&=&24 \ \mathrm {[k\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(1)
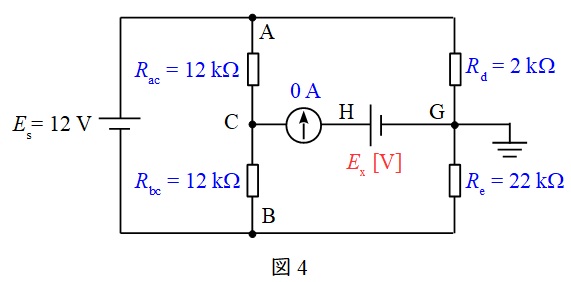
(a)解答及び題意に沿って図を描くと図4のようになる。
図4において,\( \ R_{\mathrm {d}} \ \)にかかる電圧\( \ V_{\mathrm {d}} \ \mathrm {[V]} \ \)及び\( \ R_{\mathrm {e}} \ \)にかかる電圧\( \ V_{\mathrm {e}} \ \mathrm {[V]} \ \)は,分圧の法則より,
\[
\begin{eqnarray}
V_{\mathrm {d}}&=&\frac {R_{\mathrm {d}}}{R_{\mathrm {d}}+R_{\mathrm {e}}}E_{\mathrm {s}} \\[ 5pt ]
&=&\frac {2}{2+22}\times 12 \\[ 5pt ]
&=&1 \ \mathrm {[V]} \\[ 5pt ]
V_{\mathrm {e}}&=&\frac {R_{\mathrm {e}}}{R_{\mathrm {d}}+R_{\mathrm {e}}}E_{\mathrm {s}} \\[ 5pt ]
&=&\frac {22}{2+22}\times 12 \\[ 5pt ]
&=&11 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。端子\( \ \mathrm {G} \ \)が接地され,\( \ V_{\mathrm {G}}=0 \ \mathrm {[V]} \ \)であるので,端子\( \ \mathrm {A} \ \)の電位\( \ V_{\mathrm {A}} \ \mathrm {[V]} \ \)及び端子\( \ \mathrm {B} \ \)の電位\( \ V_{\mathrm {B}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {A}}&=&V_{\mathrm {G}}+V_{\mathrm {d}} \\[ 5pt ]
&=&0+1 \\[ 5pt ]
&=&1 \ \mathrm {[V]} \\[ 5pt ]
V_{\mathrm {B}}&=&V_{\mathrm {G}}-V_{\mathrm {e}} \\[ 5pt ]
&=&0-11 \\[ 5pt ]
&=&-11 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ R_{\mathrm {bc}} \ \)にかかる電圧\( \ V_{\mathrm {cb}} \ \mathrm {[V]} \ \)は,分圧の法則より,
\[
\begin{eqnarray}
V_{\mathrm {cb}}&=&\frac {R_{\mathrm {bc}}}{R_{\mathrm {ac}}+R_{\mathrm {bc}}}E_{\mathrm {s}} \\[ 5pt ]
&=&\frac {12}{12+12}\times 12 \\[ 5pt ]
&=&6 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
なので,端子\( \ \mathrm {C} \ \)の電位\( \ V_{\mathrm {C}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {C}}&=&V_{\mathrm {B}}+V_{\mathrm {cb}} \\[ 5pt ]
&=&-11+6 \\[ 5pt ]
&=&-5 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となり,未知の直流電源の電圧\( \ E_{\mathrm {x}} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {x}}&=&V_{\mathrm {H}}-V_{\mathrm {G}} \\[ 5pt ]
&=&V_{\mathrm {C}}-V_{\mathrm {G}} \\[ 5pt ]
&=&-5-0 \\[ 5pt ]
&=&-5 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは