《理論》〈電気回路〉[H28:問5]電池を並列接続した回路における抵抗での消費電力に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図のように，内部抵抗\( \ r=0.1 \ \mathrm {\Omega } \ \)，起電力\( \ E=9 \ \mathrm {V} \ \)の電池\( \ 4 \ \)個を並列に接続した電源に抵抗\( \ R=0.5 \ \mathrm {\Omega } \ \)の負荷を接続した回路がある。この回路において，抵抗\( \ R=0.5 \ \mathrm {\Omega } \ \)で消費される電力の値\( \ \mathrm {[ W ] } \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

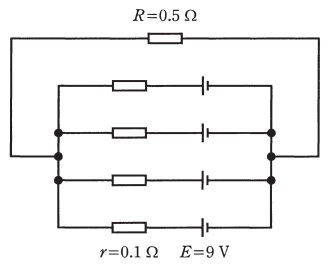
(1)　\( \ 50 \ \)　　(2)　\( \ 147 \ \)　　(3)　\( \ 253 \ \)　　(4)　\( \ 820 \ \)　　(5)　\( \ 4050 \ \)

【ワンポイント解説】

本問は電圧源から電流源へ等価変換をすれば解けます。テブナンの定理で解いても大丈夫です。

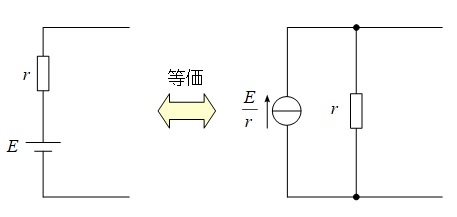
1.電圧源と電流源の等価変換
下図に示すように，電圧源と直列抵抗は電流源と並列抵抗に等価変換することができます。この時，電流源の電流の大きさは\( \ \displaystyle \frac {E}{r} \ \)となります。

【関連する「電気の神髄」記事】

　　重ね合わせの理の証明

【解答】

解答：(2)
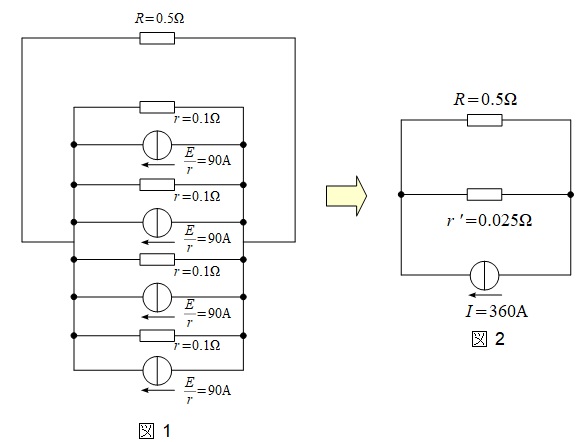
電圧源と内部抵抗を電流源に等価変換すると図1の通りとなり，さらに整理すると図2のようになる。この時\( \ R \ \)に流れる電流\( \ I_{\mathrm {R}} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {R}}&=&\frac {r’}{R+r’}I \\[ 5pt ] &=&\frac {0.025}{0.5+0.025}\times 360 \\[ 5pt ] &≒&17.14 \ \mathrm {A} \\[ 5pt ] \end{eqnarray}
\] よって，抵抗\( \ R \ \)で消費される電力\( \ W_{\mathrm {R}} \ \)は，
\[
\begin{eqnarray}
W_{\mathrm {R}}&=&RI_{\mathrm {R}}^{2} \\[ 5pt ] &=&0.5\times 17.14^{2} \\[ 5pt ] &≒&147 \ \mathrm {W} \\[ 5pt ] \end{eqnarray}
\] と求められる。