Contents
【問題】
【難易度】★★★☆☆(普通)
図のように線間電圧\( \ 200 \ \mathrm {V} \ \),周波数\( \ 50 \ \mathrm {Hz} \ \)の対称三相交流電源に\( \ \mathrm {RLC} \ \)負荷が接続されている。\( \ R=10 \ \mathrm {\Omega } \ \),電源角周波数を\( \ \omega \ \mathrm {[rad/s]} \ \)として,\( \ \omega L=10 \ \mathrm {\Omega } \ \),\( \ \displaystyle \frac {1}{\omega C}=20 \ \mathrm {\Omega } \ \)である。次の(a)及び(b)の問に答えよ。
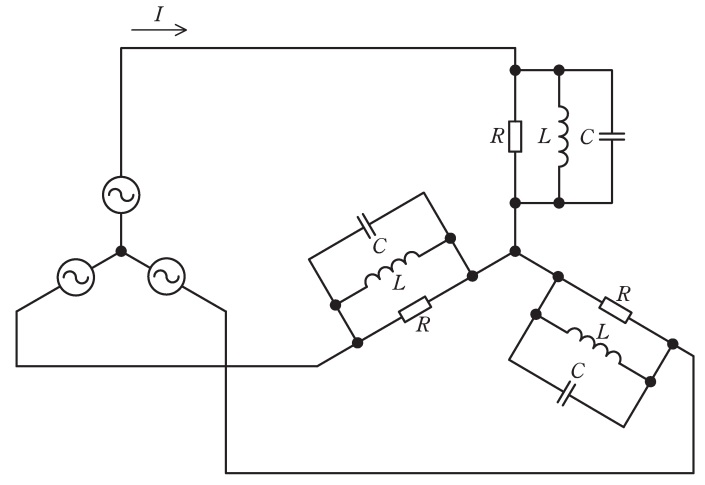
(a) 電源電流\( \ I \ \)の値\( \ \mathrm {[A]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 7 \ \) (2) \( \ 10 \ \) (3) \( \ 13 \ \) (4) \( \ 17 \ \) (5) \( \ 22 \ \)
(b) 三相負荷の有効電力の値\( \ \mathrm {[kW]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 1.3 \ \) (2) \( \ 2.6 \ \) (3) \( \ 3.6 \ \) (4) \( \ 4.0 \ \) (5) \( \ 12 \ \)
【ワンポイント解説】
三相平衡回路の場合は,まず一相分の等価回路を描くことがポイントとなります。一相分の等価回路を描く場合は線間電圧を相電圧(\( \ 1/\sqrt {3}倍 \ \))に変換する必要があります。本問は三相回路の問題としては比較的取り組みやすい問題となりますので,練習問題としてはとても良いと思います。
1.コイルやコンデンサのリアクタンス
インダクタンスが\( \ L \ \mathrm {[H]} \ \)のコイル及び静電容量が\( \ C \ \mathrm {[F]} \ \)のコンデンサを周波数\( \ f \ \mathrm {[Hz]} \ \)の交流電源に接続した時のそれぞれのリアクタンスの大きさ\( \ X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)及び\( \ X_{\mathrm {C}} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {L}}&=&\mathrm {j}\omega L \\[ 5pt ]
&=&\mathrm {j}2\pi f L \\[ 5pt ]
-\mathrm {j}X_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C} \\[ 5pt ]
&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ]
\end{eqnarray}
\]
となります。\( \ -\mathrm {j} \ \)と\( \ \displaystyle \frac {1}{\mathrm {j}} \ \)は,
\[
\begin{eqnarray}
\frac {1}{\mathrm {j}}&=&\frac {1}{\mathrm {j}}\times \frac {\mathrm {j}}{\mathrm {j}} \\[ 5pt ]
&=&\frac {\mathrm {j}}{-1} \\[ 5pt ]
&=&-\mathrm {j} \\[ 5pt ]
\end{eqnarray}
\]
となり,数学的に全く同じ値になります。
2.平衡三相負荷の有効電力
平衡三相負荷の有効電力は抵抗で消費される電力であり,一相あたりの消費電力\( \ P_{1} \ \)は,
\[
\begin{eqnarray}
P_{1}&=&RI^{2} \\[ 5pt ]
&=&\frac {V^{2}}{R} \\[ 5pt ]
\end{eqnarray}
\]
となり,三相負荷での消費電力\( \ P_{3} \ \)は,
\[
\begin{eqnarray}
P_{3}&=&3P_{1} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(a)解答:(3)
問題図の回路は三相平衡負荷であり,ワンポイント解説「1.コイルやコンデンサのリアクタンス」より,コイル及びコンデンサのリアクタンス\( \ X_{\mathrm {L}} \ \)及び\( \ X_{\mathrm {C}} \ \)は,
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {L}}&=&\mathrm {j}\omega L \\[ 5pt ]
&=&\mathrm {j}10 \ \mathrm {[\Omega ]} \\[ 5pt ]
-\mathrm {j}X_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C} \\[ 5pt ]
&=&-\mathrm {j}20 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,一相あたりの等価回路は図1のようになる。
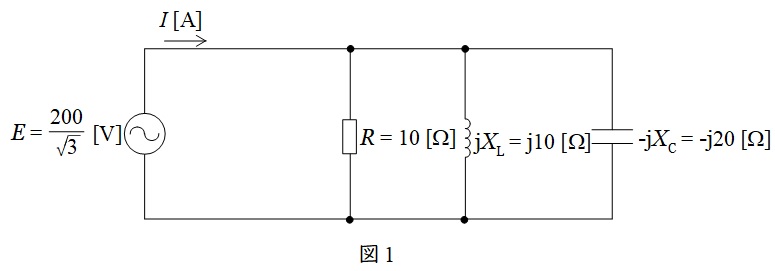
図1より,\( \ \mathrm {RLC} \ \)負荷に流れるそれぞれの電流\( \ {\dot I}_{\mathrm {R}} \ \),\( \ {\dot I}_{\mathrm {L}} \ \),\( \ {\dot I}_{\mathrm {C}} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {R}}&=&\frac {\displaystyle \frac {200}{\sqrt {3}}}{10} \\[ 5pt ]
&=&\frac {20}{\sqrt {3}} \ \mathrm {[A]} \\[ 5pt ]
{\dot I}_{\mathrm {L}}&=&\frac {\displaystyle \frac {200}{\sqrt {3}}}{\mathrm {j}10} \\[ 5pt ]
&=&-\mathrm {j}\frac {20}{\sqrt {3}} \ \mathrm {[A]} \\[ 5pt ]
{\dot I}_{\mathrm {C}}&=&\frac {\displaystyle \frac {200}{\sqrt {3}}}{-\mathrm {j}20} \\[ 5pt ]
&=&\mathrm {j}\frac {10}{\sqrt {3}} \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,電源を流れる電流\( \ \dot I \ \)は,
\[
\begin{eqnarray}
\dot I&=&{\dot I}_{\mathrm {R}}+{\dot I}_{\mathrm {L}}+{\dot I}_{\mathrm {C}} \\[ 5pt ]
&=&\frac {20}{\sqrt {3}}-\mathrm {j}\frac {20}{\sqrt {3}}+\mathrm {j}\frac {10}{\sqrt {3}} \\[ 5pt ]
&=&\frac {20}{\sqrt {3}}-\mathrm {j}\frac {10}{\sqrt {3}} \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となり,その大きさは,
\[
\begin{eqnarray}
I&=&\sqrt {\left( \frac {20}{\sqrt {3}}\right) ^{2}+\left( \frac {10}{\sqrt {3}}\right) ^{2}} \\[ 5pt ]
&=&\sqrt { \frac {400}{3}+ \frac {100}{3}} \\[ 5pt ]
&=&\sqrt { \frac {500}{3}} \\[ 5pt ]
&≒&12.9 → 13 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(4)
図1より,一相あたりの有効電力\( \ P_{1} \ \)は,ワンポイント解説「2.平衡三相負荷の有効電力」の通り,
\[
\begin{eqnarray}
P_{1}&=&\frac {V^{2}}{R} \\[ 5pt ]
&=&\frac {\left( \displaystyle \frac {200}{\sqrt {3}}\right) ^{2}}{10} \\[ 5pt ]
&=&\frac {4000}{3} \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
であるので,三相負荷の有効電力\( \ P_{3} \ \)は,
\[
\begin{eqnarray}
P_{3}&=&3P_{1} \\[ 5pt ]
&=&4000 \ \mathrm {[W]} → 4 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは