Contents
【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,帯電した導体球に関する記述である。
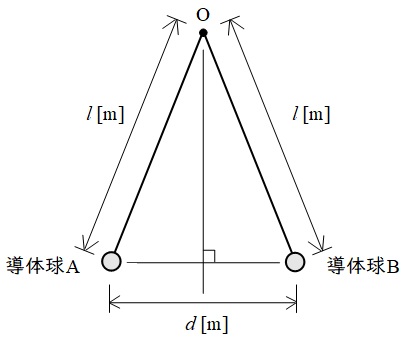
真空中で導体球\( \ \mathrm {A} \ \)及び\( \ \mathrm {B} \ \)が軽い絶縁体の糸で固定点\( \ \mathrm {O} \ \)からつり下げられている。真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \),重力加速度を\( \ g \ \mathrm {[m / s^{2}]} \ \)とする。\( \ \mathrm {A} \ \)及び\( \ \mathrm {B} \ \)は同じ大きさと質量\( \ m \ \mathrm {[kg]} \ \)をもつ。糸の長さは各導体球の中心点が点\( \ \mathrm {O} \ \)から距離\( \ l \ \mathrm {[m]} \ \)となる長さである。
まず,導体球\( \ \mathrm {A} \ \)及び\( \ \mathrm {B} \ \)にそれぞれ電荷\( \ Q \ \mathrm {[C]} \ \),\( \ 3Q \ \mathrm {[C]} \ \)を与えて帯電させたところ,静電力による\( \ \fbox { (ア) } \ \)が生じ,図のように\( \ \mathrm {A} \ \)及び\( \ \mathrm {B} \ \)の中心点間が\( \ d \ \mathrm {[m]} \ \)離れた状態で釣り合った。ただし,導体球の直径は\( \ d \ \)に比べて十分に小さいとする。このとき,個々の導体球において,静電力\( \ F=\fbox { (イ) } \ \mathrm {[N]} \ \),重力\( \ mg \ \mathrm {[N]} \ \),糸の張力\( \ T \ \mathrm {[N]} \ \),の三つの力が釣り合っている。三平方の定理より\( \ F^{2}+\left( mg \right) ^{2}=T^{2} \ \)が成り立ち,張力の方向を考えると\( \ \displaystyle \frac {F}{T} \ \)は\( \ \displaystyle \frac {d}{2l} \ \)に等しい。これらより\( \ T \ \)を消去し整理すると,\( \ d \ \)が満たす式として,
\[
\begin{eqnarray}
k\left( \frac {d}{2l}\right) ^{3}&=&\sqrt {1-\left( \frac {d}{2l}\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
が導かれる。ただし,係数\( \ k=\fbox { (ウ) } \ \)である。
次に,\( \ \mathrm {A} \ \)と\( \ \mathrm {B} \ \)とを一旦接触させたところ\( \ \mathrm {AB} \ \)間で電荷が移動し,同電位となった。そして\( \ \mathrm {A} \ \)と\( \ \mathrm {B} \ \)とが力の釣合いの位置に戻った。接触前に比べ,距離\( \ d \ \)は\( \ \fbox { (エ) } \ \)した。
上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{array}{ccccc}
& (ア) & (イ) & (ウ) & (エ) \\
\hline
(1) & 反発力 & \displaystyle \frac {3Q^{2}}{4\pi \varepsilon _{0} d^{2}} & \displaystyle \frac {16\pi \varepsilon _{0} l^{2}mg}{3Q^{2}} & 増加 \\
\hline
(2) & 吸引力 & \displaystyle \frac {Q^{2}}{4\pi \varepsilon _{0} d^{2}} & \displaystyle \frac {4\pi \varepsilon _{0} l^{2}mg}{Q^{2}} & 増加 \\
\hline
(3) & 反発力 & \displaystyle \frac {3Q^{2}}{4\pi \varepsilon _{0} d^{2}} & \displaystyle \frac {4\pi \varepsilon _{0} l^{2}mg}{Q^{2}} & 増加 \\
\hline
(4) & 反発力 & \displaystyle \frac {Q^{2}}{4\pi \varepsilon _{0} d^{2}} & \displaystyle \frac {16\pi \varepsilon _{0} l^{2}mg}{3Q^{2}} & 減少 \\
\hline
(5) & 吸引力 & \displaystyle \frac {Q^{2}}{4\pi \varepsilon _{0} d^{2}} & \displaystyle \frac {4\pi \varepsilon _{0} l^{2}mg}{Q^{2}} & 減少 \\
\hline
\end{array}
\]
【ワンポイント解説】
クーロンの法則を基本とした計算問題です。(ア),(イ),(エ)は標準的な問題ですが,(ウ)の計算がやや面倒な問題です。(ア),(イ),(エ)が分かっても(ウ)が分からなければ選択肢は一つに絞れないので,やや難しめの問題であると思います。
1.クーロンの法則
真空中で距離\( \ r \ \mathrm {[m]} \ \)離れた二つの電荷\( \ Q_{\mathrm {A}} \ \mathrm {[C]} \ \),\( \ Q_{\mathrm {B}} \ \mathrm {[C]} \ \)に加わる力\( \ F \ \mathrm {[N]} \ \)は,真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)とすると,
\[
\begin{eqnarray}
F &=&\frac {Q_{\mathrm {A}}Q_{\mathrm {B}}}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。このとき,\( \ Q_{\mathrm {A}} \ \),\( \ Q_{\mathrm {B}} \ \)の\( \ + \ \)\( \ – \ \)の符号が同符号である場合には斥力(反発する力),異符号である場合には引力(引き合う力)が働きます。
また,比例定数\( \ \displaystyle k=\frac {1}{4\pi \varepsilon _{0}}≒9\times 10^{9} \ \mathrm {[N\cdot m^{2}/C^{2}]} \ \)として,
\[
\begin{eqnarray}
F &=&k\frac {Q_{\mathrm {A}}Q_{\mathrm {B}}}{r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
とする場合もあります。
【解答】
解答:(1)
(ア)
題意より各導体球に与えられている電荷はともに+なので反発力となる。
(イ)
ワンポイント解説「1.クーロンの法則」の法則より,各導体球に働く静電力\( \ F \ \mathrm {[N]} \)は,
\[
\begin{eqnarray}
F &=&\frac {Q\times 3Q}{4\pi \varepsilon _{0}d^{2}} \\[ 5pt ]
&=&\frac {3Q^{2}}{4\pi \varepsilon _{0}d^{2}} \\[ 5pt ]
\end{eqnarray}
\]
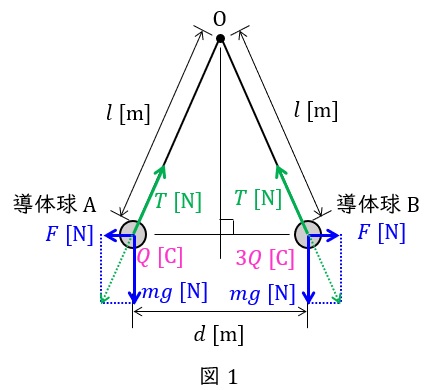
となる。このとき,静電力\( \ F \ \mathrm {[N]} \),重力\( \ mg \ \mathrm {[N]} \),張力\( \ T \ \mathrm {[N]} \)は図1のように描ける。
(ウ)
図1より,
\[
\begin{eqnarray}
\frac {F}{T} &=&\frac {\displaystyle \frac {d}{2}}{l} \\[ 5pt ]
&=&\frac {d}{2l} \\[ 5pt ]
T&=&\frac {2l}{d}F
\end{eqnarray}
\]
であるから,これを\( \ F^{2}+\left( mg \right) ^{2}=T^{2} \ \)の式に整理して代入すると,
\[
\begin{eqnarray}
F^{2}+\left( mg \right) ^{2} &=&T^{2} \\[ 5pt ]
\left( \frac {F}{T}\right) ^{2} +\left( \frac {mg}{T}\right) ^{2}&=&1 \\[ 5pt ]
\left( \frac {d}{2l}\right) ^{2} +\left( \frac {mgd}{2lF}\right) ^{2}&=&1 \\[ 5pt ]
\left( \frac {mgd}{2lF}\right) ^{2}&=&1-\left( \frac {d}{2l}\right) ^{2} \\[ 5pt ]
\frac {mgd}{2lF}&=&\sqrt {1-\left( \frac {d}{2l}\right) ^{2}} \\[ 5pt ]
\frac {mgd}{2l}\cdot \frac {4\pi \varepsilon _{0}d^{2}}{3Q^{2}}&=&\sqrt {1-\left( \frac {d}{2l}\right) ^{2}} \\[ 5pt ]
\frac {4\pi \varepsilon _{0}mg}{3Q^{2}}\cdot \frac {d^{3}}{2l}&=&\sqrt {1-\left( \frac {d}{2l}\right) ^{2}} \\[ 5pt ]
\frac {4\pi \varepsilon _{0}mg}{3Q^{2}}\cdot \left( \frac {d}{2l}\right) ^{3}\cdot 4l^{2}&=&\sqrt {1-\left( \frac {d}{2l}\right) ^{2}} \\[ 5pt ]
\frac {16\pi \varepsilon _{0}l^{2}mg}{3Q^{2}}\cdot \left( \frac {d}{2l}\right) ^{3}&=&\sqrt {1-\left( \frac {d}{2l}\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \displaystyle k=\frac {16\pi \varepsilon _{0}l^{2}mg}{3Q^{2}} \ \)と求められる。
(エ)
一旦接触させると,導体球\( \ \mathrm {B} \ \)から導体球\( \ \mathrm {A} \ \)に電荷が移動し,両方の電荷が等しくなり,共に\( \ 2Q \ \mathrm {[C]} \ \)となる。よって,\( \ \mathrm {AB} \ \)間の距離が\( \ d^{\prime } \ \mathrm {[m]} \ \)になったとすると,ワンポイント解説「1.クーロンの法則」より,各導体球に働く静電力\( \ F \ \mathrm {[N]} \ \)は,
\[
\begin{eqnarray}
F &=&\frac {2Q\times 2Q}{4\pi \varepsilon _{0}{d^{\prime }}^{2}} \\[ 5pt ]
&=&\frac {4Q^{2}}{4\pi \varepsilon _{0}{d^{\prime }}^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,(イ)の解答と比較すると\( \ d^{\prime } > d \ \)とならなければ釣り合わないので,距離は増加する。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは