《理論》〈電気回路〉[R01:問9]RLC並列回路の角周波数変化に対する電流値の変動に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

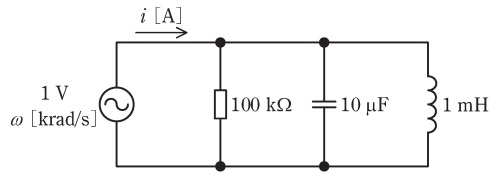
図は，実効値が\( \ 1 \ \mathrm {V} \ \)で角周波数\( \ \omega \ \mathrm {[krad／s ]} \ \)が変化する正弦波交流電源を含む回路である。いま，\( \ \omega \ \)の値が\( \ \omega _{1} = 5 \mathrm {krad／s } \ \)，\( \ \omega _{2} = 10 \mathrm {krad／s } \ \)，\( \ \omega _{3} = 30 \mathrm {krad／s } \ \)と3通りの場合を考え，\( \ \omega =\omega _{\mathrm {k}}\left( k=1，2，3\right) \ \)のときの電流\( \ i \ \mathrm {[A]} \ \)の実効値を\( \ I_{\mathrm {k}} \ \)と表すとき，\( \ I_{1} \ \)，\( \ I_{2} \ \)，\( \ I_{3} \ \)の大小関係として，正しいものを次の(1)～(5)のうちから一つ選べ。

　(1)　\(I_{1}＜I_{2}＜I_{3}\)　　(2)　\(I_{1}=I_{2}＜I_{3}\)　　(3)　\(I_{2}＜I_{1}＜I_{3}\)
　(4)　\(I_{2}＜I_{1}=I_{3}\)　　(5)　\(I_{3}＜I_{2}＜I_{1}\)

【ワンポイント解説】

それぞれ真面目に電流値を求めても導出することができますが，試験時間を考慮すると，できるだけ計算量の少ない方法を選択するのが良いと思います。本問の場合はインピーダンスではなくアドミタンスを使用する，共振条件を利用する方法が最も早く正答を導き出せると思います。

1.直列回路の共振条件
共振条件は電圧と電流が同位相になる状態で，回路のリアクタンスが零になる状態のことを言います。\( \ RLC \ \)直列回路のリアクタンスの共振条件は，角周波数を\( \ \omega =2\pi f \ \)とすると，
\[
\begin{eqnarray}
\mathrm {j}\omega L +\frac {1}{\mathrm {j}\omega C}&=&0 \\[ 5pt ] \mathrm {j}\left( \omega L -\frac {1}{\omega C}\right) &=& 0 \\[ 5pt ] \omega L &=& \frac {1}{\omega C} \\[ 5pt ] \end{eqnarray}
\] の時共振となり，その共振角周波数と共振周波数は，上式を\( \ \omega \ \)について整理すると，
\[
\begin{eqnarray}
\omega ^{2}&=&\frac {1}{LC} \\[ 5pt ] \omega &=&\frac {1}{\sqrt {LC}} \\[ 5pt ] f &=&\frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

2.並列回路の共振条件
共振条件は電圧と電流が同位相になる状態で，回路のサセプタンスが零(リアクタンスが無限大)になる状態のことを言います。\( \ RLC \ \)並列回路の共振条件は，角周波数を\( \ \omega =2\pi f \ \)とすると，
\[
\begin{eqnarray}
\mathrm {j}\omega C +\frac {1}{\mathrm {j}\omega L}&=&0 \\[ 5pt ] \mathrm {j}\left( \omega C -\frac {1}{\omega L}\right) &=& 0 \\[ 5pt ] \omega C &=& \frac {1}{\omega L} \\[ 5pt ] \end{eqnarray}
\] の時共振となり，その共振角周波数と共振周波数は，
\[
\begin{eqnarray}
\omega &=&\frac {1}{\sqrt {LC}} \\[ 5pt ] f &=&\frac {1}{2\pi \sqrt {LC}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【関連する「電気の神髄」記事】

　　直列共振回路の理論
　　並列共振回路の理論

【解答】

解答：(3)
問題図のアドミタンス\( \ \dot Y \ \)とその大きさ\( \ Y \ \)は，
\[
\begin{eqnarray}
\dot Y &=&\frac {1}{R}+\mathrm {j}\left( \omega C -\frac {1}{\omega L}\right) \\[ 5pt ] Y &=&\sqrt {\left( \frac {1}{R}\right) ^{2}+\left( \omega C -\frac {1}{\omega L}\right) ^{2} } \\[ 5pt ] \end{eqnarray}
\] であり，電流\( \ I \ \)の大きさは，
\[
\begin{eqnarray}
I &=&VY \\[ 5pt ] \end{eqnarray}
\] であるから，アドミタンス\( \ Y \ \)が大きければ大きいほど電流\( \ I \ \)は大きくなる。さらにアドミタンスの抵抗分は角周波数によって変化しないので，\( \ \displaystyle \omega C -\frac {1}{\omega L} \ \)の絶対値が大きければ大きいほど電流値が大きくなる。ワンポイント解説「2.並列回路の共振条件」より，アドミタンスが最小となる共振角周波数\( \ \omega _{\mathrm {r}} \ \)は，
\[
\begin{eqnarray}
\omega _{\mathrm {r}} &=&\frac {1}{\sqrt {LC}} \\[ 5pt ] &=&\frac {1}{\sqrt {1\times 10^{-3}\times 10\times 10^{-6}}} \\[ 5pt ] &=&\frac {1}{\sqrt {10^{-8}}} \\[ 5pt ] &=&\frac {1}{10^{-4}} \\[ 5pt ] &=&10^{4} \ \mathrm {[rad／s]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ I_{2} \ \)が最小となることが分かる。\( \ \omega _{1} \ \)及び\( \ \omega _{3} \ \)の時の\( \ \displaystyle \omega C -\frac {1}{\omega L} \ \)の絶対値を求めると，
\[
\begin{eqnarray}
\left| \omega _{1} C -\frac {1}{\omega _{1} L}\right| &=&\left| 5\times 10^{3}\times 10\times 10^{-6}-\frac {1}{5\times 10^{3}\times 1\times 10^{-3}}\right| \\[ 5pt ] &=&\left| 5\times 10^{-2}-\frac {1}{5}\right| \\[ 5pt ] &=&0.15 \\[ 5pt ] \left| \omega _{3} C -\frac {1}{\omega _{3} L}\right| &=&\left| 30\times 10^{3}\times 10\times 10^{-6}-\frac {1}{30\times 10^{3}\times 1\times 10^{-3}}\right| \\[ 5pt ] &=&\left| 0.3-\frac {1}{30}\right| \\[ 5pt ] &≒&0.267 \\[ 5pt ] \end{eqnarray}
\] となり，\( \ I_{1}＜I_{3} \ \)となることが分かる。よって，\(I_{2}＜I_{1}＜I_{3}\)と求められる。